KSZTAŁTY I ROZMIARY ZIEMI

WYKONAŁ: Piotr Szybilski

I TM Db

ZIEMIA- jedna z planet w Układzie Słonecznym, trzecia wg odległości od Słońca, piata co do wielkości, kształtem zbliżona do ogromnej kuli, wobec rozmiarów wszechświata znikomo mała niby pyłek, ale niezmiernie ważna, bo ludzkość na jej powierzchni powstała, na jej powierzchni żyje i - mimo udanych podróży pozaziemskich - jest z nie jak najściślej związana. Kula ziemska to potocznie określenie bryły ziemskiej z pominięciem jej gazowej powłoki. W rzeczywistości bryła ziemska nie ma kształtu kuli, chociaż jest do niej bardzo zbliżona, co pozwala na przyjęcie jej kulistego kształtu w wielu rozważaniach geodezyjnych i geograficznych. Rzeczywista, fizyczna powierzchnia jest urozmaicona wzniesieniami i obniżeniami terenu. Nawet jednak wyobrażona powierzchnia, która by powstała, gdybyśmy usunęli wszelkie nierówności ludów od poziomu, nie byłaby kula lecz nieregularna bryła, określona nazwa geoidu. Geoid, geoida jest to bryła ziemska tak pomyślana, że w każdym miejscu jej powierzchnia jest pozioma, a więc prostopadła do kierunku działania siły ciężkości, a na morzach znajduje się na średnim poziomie mórz. Geoida jest bardzo zbliżona do elipsoidy obrotowej, odbiega od niej miejscami o wysokość od +127 do 160m. Elipsoidę przyjmuje się jako kształt ziemi w pracach geodezyjnych i kartograficznych. Elipsoida jest to bryła powstała przez obrót elipsy wokół jej małej osi. Taki kształt przyjmuje się w rozważaniach geodezyjnych ponieważ przyjęcie nieregularnego kształtu geoidy lub fizycznej powierzchni Ziemi stwarzałoby duże trudności w obliczeniach geodezyjnych i kartograficznych.

Argumenty przemawiające za kulistością Ziemi znane były już w starożytności, a więc w okresie, w który panowało ogólne przekonanie o płaskim kształcie Ziemi. Jednym z nich może być widok statków zbliżających się do wybrzeża morskiego. Podczas takiego zbliżania dostrzegamy najpierw wierzchołki masztów, a potem dopiero stopniowo coraz niżej położone części statków, dopóki statki nie wyłonią się w całości dla obserwatora stojącego na wybrzeżu. Na kulisty, w przybliżeniu, kształt Ziemi wskazuje również to, że widnokrąg na morzu i równinach jest łukiem, którego promień wzrasta ze wzrostem wzniesienia obserwatora nad powierzchnia Ziemi. Wreszcie o zakrzywieniu powierzchni Ziemi pouczają nas zmiany wysokości bieguna towarzyszące przemieszczaniu się obserwatora wzdłuż południka geograficznego, przy czym równym przemieszczeniom obserwatora odpowiadają prawie równe zmiany wysokości bieguna względem horyzontu. Z dostatecznym przeto uzasadnieniem w pierwszym przybliżeniu możemy uważać Ziemię za kulę.

Na podstawie tego założenia już w starożytności dokonano pierwszych pomiarów łuku południka ziemskiego i rozmiarów kuli ziemskiej. Uczynił to Eratostenes w trzecim wieku p.n.e. Tok rozumowania Eratostenesa był następujący: wybieramy na południku dwa punkty A i B dostatecznie różniące się pod względem szerokości geograficznej. Jeżeli zmierzymy odległość łuku południka geograficznego między tymi punktami i będziemy znać różnicę szerokości geograficznej, to możemy wyznaczyć promień Ziemi, zgodnie z rys. 1. Z następującej proporcji:

S/2*3,14*R=(φB-φA)/360°

S- długość zmierzonego łuku

R- promień Ziemi

φA, φB- szerokość geograficzna punktów A i B

Eratostenes zwrócił uwagę na to że w miejscowości Syene (obecnie Assuan w Egipcie), Słońce w dniu stanowiska letniego w południe nie rzuca cienia, czyli jest w zenicie i może być widziane z dna najgłębszych studzien, pod czas, gdy Aleksandrii, położonej w przybliżeniu na tym samym południku co Syene bywa nawet w odległości zenitalnej równej 1/50 obwodu koła, czyli 7,2 °. Eratostenes obliczył, że obwód Ziemi wynosi 2*3,14*R=250000 stadionów, czyli, ze promień Ziemi R=40000 stadionów. Jeżeli przyjmiemy ,że 1 stadion to 157,7m to R obliczony przez Eratostenesa wynosi blisko 6300km, co jest w dobrej zgodności z wartością rzeczywista. Powyższe obliczenia mówią o tym, jak z pomiaru łuku południka przy znajomości szerokości geograficznej jego końców można obliczyć promień Ziemi. Promień ten obliczamy tym dokładniej im dłuższy łuk południka uda nam się zmierzyć jednostkami długości. Bezpośrednie pomiary długości łuków na powierzchni Ziemi byłyby bardzo żmudne i niepewne ze względu na nierówności terenu i przeszkody naturalne. Z tego powodu długość łuk południka wyznaczamy w sposób pośredni przy pomocy triangulacji. Aby zmierzyć długość łuku południka metoda triangulacji, wybieramy w jego pobliżu punkty A, B, C... odległe od siebie zwykle o kilkadziesiąt km i dobrane tak, aby z każdego punktu można byłoby widzieć dwa inne. Tego rodzaju punkty tworzy sieć trójkątów, w których wymierzamy kąty, za pomocą teodoidu, instrumentu przeznaczonego do mierzenia katów poziomych. W sieci trójkątów wybieramy jeden bok lub odcinek pomocniczy zwany baza, aby go zmierzyć miarami długości. Wyznaczamy przy tym z obserwacji astronomicznych jego azymut. Znając długość bazy i azymuty wszystkich boków trójkąta, a więc również i ich rzuty na południk. W końcowych wierzchołkach sieci triangulacyjnej, a często i w punktach pośrednich, wyznaczamy z obserwacji astronomicznych szerokość geograficzna. Wierzchołki te mogą nie leżeć na jednym południku. Wtedy przy wyznaczaniu długości południka przechodzącego przez pierwszy wierzchołek prowadzimy przez drugi końcowy wierzchołek sieci równoleżnik. Szukaną przez nas długością łuku południka będzie łączący pierwszy wierzchołek z punktem przecięcia się południka i równoleżnika poprowadzonego przez drugi wierzchołek. Po podstawieniu otrzymanej wartości do wzoru nr 1. Możemy obliczyć R Ziemi.

Gdyby Ziemia miała kształt dokładnie kulisty, to pomiary łuków południka powinny dawać jednakowa wartość na promień Ziemi niezależnie od szerokości geograficznej mierzonego łuku. W związku z ruchem obrotowym Ziemi dookoła osi i występująca, na skutek tego siła odśrodkowa należałoby się spodziewać, że Ziemia byłaby bryła spłaszczona na biegunach. Dowodu na to powinna dostarczyć triangulacja przeprowadzona w różnych szerokościach geograficznych.

Promień obliczany na podstawie pomiarów triangulacyjnych jest średnią wartością tzw. promienia krzywizny łuku południka między jego krańcowymi wartościami φ_A i φ_B. Jeżeli na dowolnej krzywej płaskiej wybierzemy trzy punkty i poprowadzimy przez nie koło, to gdy skrajne punkty zmierzać będą do punktu środkowego, to poprowadzone przez nie łuki kół będą zmierzać do pewnego granicznego koła, które nazywać będziemy kołem krzywizny w środkowym punkcie łuku. Promień tego koła nosi nazwę promienia krzywizny. Jeżeli pojęcia te zastosujemy do południka, to wyznaczone w ten sposób promienie Ziemi będą wyrażały średnią wartość promienia krzywizny południka na mierzonym łuku. Zmienna krzywizna południka powoduje, że długości łuków odpowiadających różnicy szerokości geograficznej o 1 ° będą również się zmieniały wraz z szerokością geograficzna. Np. gdyby Ziemia miała kształt zbliżony do elipsoidy spłaszczonej na biegunach, promień krzywizny południka blisko bieguna byłby większy niż blisko równika, choć promień Ziemi na biegunie jest mniejszy niż na równiku. Gdyby Ziemia miała kształt elipsoidy obrotowej wydłużonej wzdłuż osi obrotu, byłoby wręcz odwrotnie. Zagadnienie to powinna rozstrzygnąć triangulacja.

Początkowo pomiary triangulacyjne, wykonywane we Francji w siedemnastym wieku, zdawały się wykazywać, że promień krzywizny maleje wraz ze wzrostem szerokości geograficznej, a więc Ziemię należałoby uważać za elipsoidę obrotowa wydłużona wzdłuż osi biegunowej. Byłoby to sprzeczne z teoria ziemskiego ruch obrotowego, wg której należało spodziewać się spłaszczenia Ziemi na biegunach. Aby móc rozstrzygnąć czy Ziemia ma kształt wydłużonej, czy spłaszczonej na biegunach elipsoidy, zorganizowano w latach 1735-1742 dwie ekspedycje triangulacyjne, jedna do obszaru blisko kręgu polarnego w Laponii, druga do obszaru równikowego w Peru. Opracowanie trzech triangulacji w Laponii(śr. szerokość geograficzna łuku φ=66°,we Francji φ=49° i w Peru φ=-2°) wykazało definitywnie, że łuk południka odpowiadający różnicy 1° w szerokości geograficznej jest najdłuższy w Laponii, a najkrótszy w Peru (we Francji ma wartość pośrednik jak należało się spodziewać przy założeniu, że Ziemia ma kształt bryły spłaszczonej na biegunach.

W drugim przybliżeniu Ziemię należy uważać za spłaszczona elipsoidę obrotowa, tj. taka bryłę geometryczna, jaka otrzymujemy przez obrót elipsy dookoła jej małej

osi. Przy tym założeniu, abstrahując od nierówności ludów, południki geograficzne sa elipsami, których wspólna osi mała jest średnica biegunowa Ziemi. Jednym z naczelnych zadań geodezji jest obliczanie rozmiarów i kształtów takiej elipsoidy obrotowej, która byłaby zbliżona do powierzchni Ziemi. Wymaga to przede wszystkim dokładnej definicji, co rozumiemy pod nazwa "powierzchnia Ziemi°, wiemy bowiem, że powierzchnię fizyczna Ziemi tworzy lady zawierające liczne wzniesienia i doliny oraz morza, których poziom ulega pewnym zmianom. Jednakże poziom morza okazał się najodpowiedniejszy do określenia matematycznej powierzchni Ziemi. Wybrano więc za podstawowa powierzchnię, tzw. geoidę, będąca, powierzchnia normalna w każdym punkcie do kierunku siły ciężkości na średnim poziomie oceanów w stanie spoczynku, czyli uwolnionym od wpływów falowania i działania wiatrów. Geoida jest powierzchnia nieregularna, kształt jej bowiem zależy od rozmieszczenia mas wewnątrz Ziemi. Do geoidy dopasowujemy elipsoidę ziemska.

Ponieważ pomiary triangulacyjne są wykonywane na powierzchni Jadów wzniesionych nad powierzchnię oceanów, więc należ je sprowadzić je do poziomu morza, do czego potrzebna jest znajomość wzniesienia punktów triangulacyjnych

nad poziomem morza. Wzniesienie to wyznaczamy za pomocy niwelacji geodezyjnej. Kształt i rozmiary spłaszczonej elipsoidy obrotowej będą określone, jeżeli będziemy znali promień równikowy (a) i promień biegunowy (b). Zamiast tych dwóch wielkości, kształt i rozmiary elipsoidy określamy najczęściej przez promień równikowy (a) i spłaszczenie α określone ze wzoru:

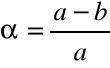
Z triangulacji, wykonywanych w różnych częściach Ziemi, wielokrotnie obliczono elementy elipsoidy ziemskiej.

Oto wymiary elipsoidy ziemskiej wg F. Krasowskiego: a- promień równikowy = 6378245m

b- promień biegunowy = 6356863m

^{a- wskaźnik spłaszczenia = 0,0033523 pole powierzchni elipsoidy = 510083059km2 objętość elipsoidy = 1083320000000km3}

Inne wartości podaje elipsoida przyjęta w 1976r na Kongresie Międzynarodowej Unii Astronomicznej:

a = 6378140m b = 6356760m

a = 0,003352813178

^{pole powierzchni = 510069000km2 objętość = 1083219000000km2}

Czynione są próby przedstawienia Ziemi w trzecim przybliżeniu za pomocy elipsoidy trójosiowej. W tym przybliżeniu równik byłby elipsa. Jednak różnica największego i najmniejszego promienia Ziemi, w odniesieniu do geoidy jest mała w porównaniu z rozmiarami Ziemi, wynosi bowiem ponad 200m. Z obserwacji sztucznych satelitów Ziemi wynika, że istnieje również niewielka różnica między promieniami biegunowymi Ziemi (północnym i południowym rzędu 20m).

BIBLIOGRAFIA: JAN FLIS- "SZKOLNY SŁOWNIK GEOGRAFICZNY EUGENIUSZ RYBKA- "ASTRONOMIA OGÓLNA" I IRM

2

---