Równanie płaszczyzny :
, gdzie
to wektor prostopadły do płaszczyzny i punkt
należy do płaszczyzny.

Równanie parametryczne prostej: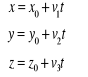
, gdzie
to wektor równoległy do prostej przechodzącej przez punkt
.

Równanie kanoniczne prostej:
, gdzie
to wektor równoległy do prostej przechodzącej przez punkt
.

Zadanie 17.

1. Mając dane trzy punkty, tworzymy dwa wektory (dowolnie ale zaczepione w jednym punkcie np. A (AB, AC) później wyznaczamy wektor prostopadły, czyli liczymy iloczyn wektorowy
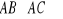
   . Powstały wektor i jeden z punktów podstawiamy do wyżej wyznaczonego równania.

2. Mając dane punkt i dwa wektory tworzymy wektor prostopadły do niech (iloczyn wektorowy) i podstawiamy do wzoru.

3. Po oczytaniu punktów należących do prostych
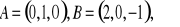
   oraz wektorów do nich równoległych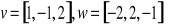
   należy wyznaczyć wektor prostopadły czyli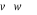
   i podstawić do równania płaszczyzny.

Zadanie 18.

Mając dane dwa punkty tworzymy wektor i podstawiamy do równania parametrycznego płaszczyzny a następnie przekształcamy równanie do postaci kanonicznej.

Zadanie 19.

Zostawiam Państwu do samodzielnego rozwiązania.