Właściwości termodynamiczne substancji rozpuszczonych w roztworze opisują cząstkowe molowe funkcje termodynamiczne. Do badania procesów równowagowych stosuje się najczęściej cząstkowe molowe entalpie swobodne składników, zwane potencjałami chemicznymi μ_i:

gdzie μ_i - potencjał chemiczny składnika i, μ_i^o - potencjał standardowy składnika i, R - stała gazowa, T - temperatura w skali bezwzględnej. Jak widać z powyższego równania aktywność jest miarą różnicy potencjału chemicznego substancji w roztworze i potencjału standardowego tej substancji. Jeżeli za stan standardowy przyjąć stan hipotetyczny , w którym stężenie substancji jest równe na przykład 1 mol/dm³ i w którym roztwór wykazuje własności roztworu nieskończenie rozcieńczonego, to aktywność będzie miarą pracy, jaką trzeba wykonać, aby 1 mol substancji przenieść z roztworu idealnego do rzeczywistego o danym stężeniu. Dla tak dobranego stanu standardowego aktywność można wyrazić jako:

Czynnik f nosi nazwę współczynnika aktywności. W przypadku roztworów elektrolitów wprowadza się pojęcie aktywności jonowych. Zgodnie z równaniem aktywność i-tych jonów jest równa zmianie entalpii swobodnej roztworu, do którego w warunkach stałej temperatury, ciśnienia i bez zmiany liczby moli innych składników dodano jeden mol jonów danego rodzaju. Ponieważ jednak musi być zachowany warunek elektroobojętności roztworu, określa się jedynie potencjał chemiczny i aktywność elektrolitu jako całości. Jeśli na przykład elektrolit dysocjuje według równania:

przy czym n₊z₊ = n_- z_-= n_e jest wartościowością elektrochemiczną elektrolitu to za aktywność elektrolitu przyjmuje się średnią geometryczną aktywności jonów, oznaczaną jako a+:

gdzie n=n₊+n_- oznacza liczbę jonów tworzących się w wyniku dysocjacji. Analogicznie określa się średnie jonowe stężenie elektrolitu c₊ oraz średni jonowy współczynnik aktywności f₊ :

W roztworach silnie rozcieńczonych (dla których stosuje się teoria Debye'a-Hückela) średnie współczynniki aktywności można obliczyć teoretycznie z równania:

gdzie: A - stała zawierająca przenikalność dielektryczną rozpuszczalnika, temperaturę, wynosząca 0.509 mol^-1/2dm^3/2 dla roztworów wodnych w temperaturze 298 K, z₊, z_- - wartościowości jonów, I - siła jonowa określona następującą zależnością:

Jeśli uwzględni się rozmiary jonów, to średnie współczynniki aktywności można wyliczyć z następującej zależności:

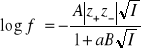
Dla elektrolitów 1-1 wartościowych równanie to stosuje się do stężeń nie przekraczających 0.1 M. Stała B zawiera stałe uniwersalne, przenikalność dielektryczną rozpuszczalnika i temperaturę, natomiast wielkość a przedstawia efektywną średnicę jonów, tj. najmniejszą odległość, na jaką mogą się zbliżyć jony różnoimienne. Jest to parametr empiryczny, zależny od rodzaju elektrolitu.

Dalsze rozszerzenie zakresu stosowalności równania Debye'a-Hückela jest możliwe przez wprowadzenie dodatkowej poprawki związanej z siłą jonową roztworu:

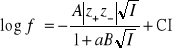
C jest współczynnikiem empirycznym.

Równanie jest nazywane równaniem Debye'a-Hückela-Brönsteda.

Teoria Debye'a-Hückela zwana jest też Teorią Elektrolitów Mocnych i tłumaczy nieprawidłowości w stężonych roztworach elektrolitów mocnych. Elektrolity mocne są zdysocjowane w każdym rozcieńczeniu. Oznacza to, że wszystkie cząsteczki np. kwasu HCl, niezależnie czy jest to kwas stężony czy rozcieńczony, ulegają rozpadowi na jony.

W roztworze elektrolitu mocnego pod wpływem oddziaływania elektrostatycznego dookoła każdego jonu powstaje tzw. chmura jonowa o ładunku przeciwnym do ładunku jonu i porusza się ona w polu elektrycznym w kierunku przeciwnym. Teoria mocnych elektrolitów w pierwotnej postaci stanowi przybliżony opis rozcieńczonych roztworów elektrolitów, dla roztworów bardziej stężonych lub mieszanin różnych elektrolitów wymaga dodatkowych uściśleń.

Jedną z najbardziej dokładnych metod wyznaczania średnich współczynników aktywności jonów elektrolitu jest pomiar siły elektromotorycznej ogniw zbudowanych z elektrod, z których jedna jest odwracalna względem kationu a druga względem anionu tego elektrolitu.

Korzystając z definicji średniej jonowej aktywności i średniego jonowego współczynnika aktywności, oraz z faktu, że dla elektrolitu 1-1 wartościowego średnie stężenie jonów jest równe stężeniu analitycznemu c, równanie można zapisać następująco:

Jeżeli wyznaczymy siłę elektromotoryczną ogniwa przy różnych stężeniach molowych kwasu i jeżeli znamy standardową siłę elektromotoryczną ogniwa, możliwe jest wyznaczenie z równania średnich jonowych współczynników aktywności kwasu dla badanych stężeń. Standardową siłę elektromotoryczną ogniwa można wyznaczyć z danych doświadczalnych. Przekształcając równanie do postaci:

oraz zamieniając logarytmy naturalne na dziesiętne i podstawiając

według równania Debye'a-Hückela-Brönsteda, otrzymujemy ostatecznie

Wykres zależności lewej strony równania od stężenia w zakresie niskich stężeń jest linią prostą, która na osi rzędnych odcina wartość E^o.

---