Akademia Techniczno-Humanistyczna
W Bielsku-Białej
OCHRONA ŚRODOWISKA
Rok I, semestr II
ĆWICZENIE Nr 13.
WYZNACZANIE PRZYŚPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO.
Wykonali:
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się z podstawowymi zagadnieniami związanymi z analizą pola grawitacyjnego Ziemi.
Część teoretyczna:
Przyśpieszeniem ziemskim nazywamy przyśpieszenie swobodnego spadku ciał pod wpływem ich ciężaru.
Zgodnie z drugą zasadą dynamiki:
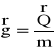
gdzie g - przyśpieszenie ziemskie, m - masa ciała.
![]()
Przyśpieszenie ziemskie zmienia się w niewielkim zakresie w różnych punktach powierzchni Ziemi ze względu na zmienność ciężaru. Ciężar jest wypadkową skierowanej do środka Ziemi siły grawitacji oraz odśrodkowej siły bezwładności spowodowanej ruchem obrotowym Ziemi wokół jej osi.
Wartość siły bezwładności oraz jej kierunek względem kierunku siły grawitacji są zależne od szerokości geograficznej.
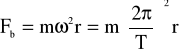
gdzie ω - prędkość kątowa ruchu obrotowego Ziemi, T - okres obiegu
Ziemi wokół jej osi, r - promień okręgu po którym porusza się
ciało,
Wahadło rewersyjne (odwracalne) - bryła sztywna, która zawieszona kolejno na dwóch osiach równoległych leżących po przeciwnych stronach jej środka ciężkości w nierównych od niego odległościach, ma taki sam okres drgań.
Przebieg ćwiczenia.
Zawieszamy wahadło na jednym z jego ostrzy - O1,przesuwamy masę M na środek pręta. Wykonujemy serię m=10 pomiarów czasu t dziesięciu drgań (n=10) bez zmiany położenia masy M. Wyniki umieszczamy
w Tab. 1 i na ich podstawie obliczamy wartość średnią t i średni błąd kwadratowy St pojedynczego pomiaru skorygowany przez odpowiedni współczynnik Studenta-Fishera: St=tα,mS't.
Tab. 1.
t1 [s] |
t2 [s] |
t3 [s] |
t4 [s] |
t5 [s] |
t6 [s] |
t7 [s] |
t8 [s] |
t9 [s] |
t10 [s] |
18,85 |
18,82 |
18,85 |
18,78 |
18,76 |
18,70 |
18,84 |
18,79 |
18,78 |
18,79 |
![]()
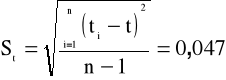
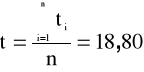
t |
S't |
tα,m |
St |
18,80 |
0,047 |
2,3 |
0,11 |
Przesuwamy masę M do ostrza swobodnego O2 i wykonujemy serię pojedynczych pomiarów czasów t' dziesięciu drgań przesuwając masę M w kierunku osi wahadła co 5 cm. Następnie obracamy wahadło
i zawieszając je na drugiej osi postępujemy jak wyżej -mierzymy czasy t'',
a wyniki notujemy w Tab. 2.
Tab.2.
Kn |
[cm] |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
T' |
[s] |
20,02 |
19,86 |
19,60 |
19,39 |
19,15 |
18,86 |
18,78 |
18,70 |
18,69 |
18,75 |
T'' |
[s] |
20,22 |
19,81 |
19,55 |
19,30 |
18,97 |
18,72 |
18,46 |
18,22 |
18,02 |
17,87 |
Kn |
[cm] |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
T' |
[s] |
18,85 |
18,90 |
18,96 |
19,11 |
19,26 |
19,49 |
19,74 |
19,89 |
20,06 |
20,32 |
T'' |
[s] |
17,64 |
17,52 |
18,61 |
17,84 |
18,28 |
18,73 |
19,29 |
19,75 |
20,08 |
20,30 |
Korzystając z wykresu odczytujemy współrzędne t'0 i t"0 punktów przecięcia się krzywych t'(kn) i t"=(kn).
t'0 =19,97 t"0 = 20,04
Obliczamy średni czas dziesięciu drgań t0 = (t'0 + t"0)/2
t0 = (19,97+20,04)/2 = 20,00
Szacujemy błąd Δ t0 ze wzoru:
![]()
gdzie: Δt'0 = |t'0 - t"0| /2
Δt'0 = 0,035
Δt0 = 0,12
Obliczamy okres drgań wahadła T0.
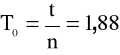
Obliczamy przyspieszenie ziemskie g i błąd bezwzględny Δg ze wzorów:
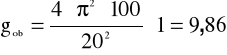
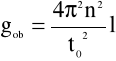
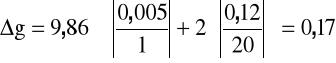
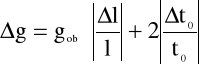
Wyniki umieszczamy w Tab. 3.
t'0=19,97 [s] |
t''0=20,04 [s] |
t0=20,00 [s] |
Δt'0=0,035 [s] |
Δt0= 0,12 [s] |
T0= 1,88 [s] |
l= 1 [m] |
Δl=0,005 [m] |
g=9,86 [m/s] |
Δg=0,17 [m/s] |
Wnioski:
Przeprowadzenie powyższego ćwiczenia pozwoliło nam na dokładniejsze zaznajomienie się z zagadnieniami dotyczącymi przyśpieszenia ziemskiego i grawitacji. Wartość siły bezwładności oraz jej kierunek względem kierunku siły grawitacji są zależne od szerokości geograficznej. Innym czynnikiem wpływającym na lokalne zmiany wartości przyśpieszenia jest zmienna gęstość Ziemi oraz wysokość nad jej powierzchnią.
Wielokrotne pomiary tej samej wielkości fizycznej daną metodą dają różne wyniki liczbowe. Błędy pomiarowe powstały wskutek niedoskonałości przyrządów , metod pomiarowych, naszych zmysłów i refleksu.
5
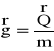
![]()
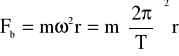
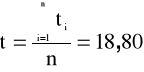
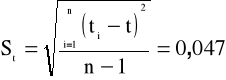
![]()
![]()
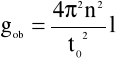
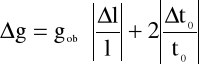
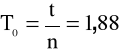
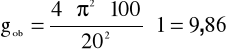
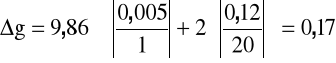
Wyszukiwarka
Podobne podstrony:
cw 85 sprawozdanie, ATH, Fizyka
cw 78 sprawozdanie, ATH, Fizyka
80 Wyznaczanie długości fali świetlnej za pomocą spektrometru siatkowego, WŁÓKIENNICTWO, Sprawozdani
cw 13, agh wimir, fizyka, Fizyka(1)
78 Wyznaczanie długości fali świetlnej metodą pierścieni Newtona, WŁÓKIENNICTWO, Sprawozdania ATH, F
15 Wyznaczanie prędkości dźwięku w powietrzu i ciałach stałych, WŁÓKIENNICTWO, Sprawozdania ATH, Fiz
FIZYKA ćw.56 badanie wpływu temp. na opór elektryczny, Sprawozdania ATH
tabele do cw 36, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
Fizyka laboratorium ćw 75 (SPRAWOZDANIE)
cw 13 fizyka
Sprawozdanie 21, Fizyka Sprawozdania, Ćw nr 21
SPR F 13, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
Fizyka cw 123 wyniki, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI -
ĆW 77- SPRAWOZDANIE, Automatyka i robotyka air pwr, III SEMESTR, FIZYKA 2, sprawko 77
sprawozdanie z cw 4, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie orga
cw 13 - Lepkosc, AGH, agh, programinski, Laborki, Laborki, Lab, FIZYKA - Laboratorium, Struna i Krzy
CW 51, pwr-eit, FIZYKA, FIZYKA H1 H2, LABORATORIUM, WSZYSTKIE SPRAWOZDANIA, ROZNE, FIZYKA LABOR, FIZ
cw 133 teoria, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawoz
Wnioski do Ćw 65b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65b
więcej podobnych podstron