ZADANIE 1

Dane :

-obciążenia charakterystyczne stałe i zmienne długotrwałe

P_n = 250 kN/m

H_n = 10 kN/m

M_n =11 kNm/m

-obciążenia obliczeniowe stałe i zmienne długotrwałe

P_r = 295 kN/m

H_r = 11 kN/m

M_r= 15 kNm/m

-warunki gruntowe

Do projektowania przyjęto :

- beton ławy B15 (γ_b⁽ⁿ⁾ = 24 kN/m³),

- stal A II , 18G2 (R_a = 310000 kPa),

- pale wiercone Wolfsholza D = 0.30 m,

- szerokość ławy 1,60 m,

- wysokość ławy 0,70 m,

1 Przyjęcie rozmieszczenia pali , wymiarów ławy , zestawienie obciążeń

Pale pod ławą rozmieszczono w dwóch rzędach . Osiowy rozstaw pali wynosi r = 1,83 m . Rozstaw rzędów pali wynosi r₁ = 0.90 m , odstęp mierzony równolegle do długości ławy l_o = 1,60 m . Wysokość ławy przyjęto h = 0.7 m .

Ponieważ na ławę działają stałe obciążenia , projektuje się przesunięcie środka ciężkości układu palowego względem osi ściany . Zaniedbując we wstępnych obliczeniach ciężar gruntu G₃ i posadzki G₂ nad odsadzkami fundamentu wyznaczono mimośród wypadkowej obciążeń M_r , H_r , P_r względem osi ściany w poziomie podstawy ławy :

Przyjęto przesunięcie środka ciężkości układu palowego względem osi ściany o e₁ = 5 cm.

Ciężar własny ławy wynosi :

- charakterystyczny G_1n = 1.6*0.7*24 = 26.88 kN/m,

- obliczeniowy G_1r = 1.1*26.88 = 29.57 kN/m.

Ciężar posadzki

- charakterystyczny G_2n = 0.7*0.15*24 = 2.52 kN/m,

- obliczeniowy G_2r = 1.3*2.52 = 3.28 kN/m.

Ciężar gruntu nasypowego nad odsadzką γ⁽ⁿ⁾_Pg = 17 kN/m³

* z lewej strony :

- charakterystyczny G_3n = 0.6*0.75*17 = 7.65 kN/m,

- obliczeniowy G_3r = 1.2*7.65 = 9.18 kN/m.

* z prawej strony :

- charakterystyczny G_4n = 0.7*0.20*17 = 2.38 kN/m,

- obliczeniowy G_4r = 1.2*2.38 = 2.86 kN/m.

Mimośród wypadkowej obciążeń względem środka ciężkości układu palowego

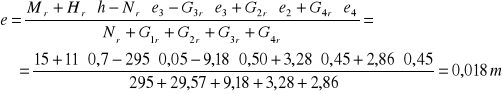
Wypadkowa obciążeń daje moment względem środka ciężkości układu palowego równy

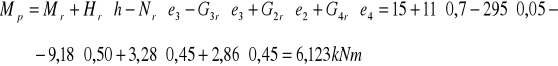
Wyznaczenie sił przypadających na poszczególne pale od obciążeń obliczeniowych

- pale rzęu pierwszego (od lewej )

R_1r = (P_r+ G_1r+G_2r+G_3r+ G_4r -(M_p / r))*l_o =

= (295+29.57+3.28+9.18+2.86-(6.123 / 0.9))*1.60 = 532.93 kN,

- pale rzędu drugiego (od lewej )

R_1r = (P_r+ G_1r+G_2r+G_3r+G_4r+(M_p / r))*l_o =

= (295+29.57+3.28+9.18+2.86+(6.123 / 0.9))*1.60 = 554.71 kN.

Średnia siła przypadająca na pale od obciążeń obliczeniowych

R_r = (P_r+ G_1r+G_2r+G_3r+G_4r))*l_o = (295+29.57+3.28+9.18+2.86)*1.60 = 543.824 kN.

2 Przyjęcie długości i obliczenie nośności pala

Nośność pala

m*Nt > R1r+Grp

Grp - ciężar własny pala

Dla pali wierconych z tab.5.7 poz.4a

S_s = 0.9 , dla piasku średniego , I_D⁽ⁿ⁾ = 0.4

S_s = 0.8 , dla gliny pylastej , I_L⁽ⁿ⁾ = 0.15

S_p = 1.0 ,

S_s = 0.9 , dla żwiru , I_D⁽ⁿ⁾ = 0.45

Pole podstawy pala (D = 0.30 m) :

Dla wszystkich warstw poziom 0.00 znajduje się w poziomie terenu,

Grubość obliczeniowych warstw (h_i) , przez które przechodzi pal oraz średnie głębokości zalegania , są następujące :

I grubość 2.05 m ,średnia głębokość zalegania 2.475 m

IIa grubość 1.1 m , średnia głębokość zalegania 4.45 m

IIb grubość 2.0 m , zalega poniżej głębokości 5.0 m, średnia głębokość zalegania 6.0 m

III zalega poniżej głębokości 7.0 m.

A. Obliczenie współczynników t_i dla średnich głębokości zalegania warstw

Warstwa I , piasek średni , I_D⁽ⁿ⁾ = 0.4 :

- dla I_D⁽ⁿ⁾ = 0.33 t = 47 kPa,

- dla I_D⁽ⁿ⁾ = 0.67 t = 74 kPa,

zatem dla I_D⁽ⁿ⁾ = 0.4

t = 47 +(74-47)*[(0.4-0.33)/(0.67-0.33)] = 52.56 kPa

- dla średniej głębokości zalegania 2.475 m

t_I = t_2.475 = 52.56*(2.475/5.0) = 26.02 kPa.

Warstwa II , glina pylasta zwięzła , I_L⁽ⁿ⁾ = 0.15 :

- dla I_L⁽ⁿ⁾ = 0 t = 50 kPa ,

- dla I_L⁽ⁿ⁾ = 0.5 t = 25 kPa ,

zatem dla I_L⁽ⁿ⁾ = 0.15

t = 25 +(50-25)*[(0.5-0.15)/0.5] = 42.5 kPa

Strop warstwy zalega na głębokości 3,9 m poniżej poziomu zastępczego. Należy wydzielić warstwę IIa zalegającą od 3,9 - 5,0 m o miąższości 1,1 m i o średniej głębokości zalegania równej 4,45 m oraz warstwę IIb poniżej 5 m o miąższości 2,0 m.

Dla warstwy IIa :

- dla średniej głębokości zalegania 4.45 m

t_Ia = t_4,45 = 42.5*(4.45/5.0) = 37.825 kPa.

Dla warstwy IIb :

t_IIb = t = 42.5 kPa.

Warstwa III , żwir , I_D⁽ⁿ⁾ = 0.45 :

- dla I_D⁽ⁿ⁾ = 0.33 t = 74 kPa,

- dla I_D⁽ⁿ⁾ = 0.67 t = 110 kPa,

zatem dla I_D⁽ⁿ⁾ = 0.45

t = 74 +(110-74)*[(0.45-0.33)/(0.67-0.33)] = 86.7 kPa

B. Obliczenie współczynnika q

Średnica pala wynosi D = 0.3 m , więc głębokość krytyczna h_c= 10 m.

Wstępnie przyjęto , że podstawa pala będzie się znajdować w żwirach na głębokości mniejszej niż 10 m poniżej poziomu zastępczego.

- dla żwiru o I_D⁽ⁿ⁾ = 0.33 q = 3000 kPa ,

- dla żwiru o I_L⁽ⁿ⁾ = 0.67 q = 5100 kPa ,

zatem dla I_D⁽ⁿ⁾ = 0.45

q₁₀ = 3000+(5100-3000)*[(0.45-0.33)/(0.67-0.33)] = 3741.17 kPa

- dla poziomu podstawy (końca) pala , oznaczając przez x zagłębienie pala w żwirach poniżej poziomu 7 m , mierzonego od poziomu zastępczego :

q_x = (7+x)*(q₁₀/10) = (7+x)*( 3741.17/10) = 2618.84 + 374.12*x

Powierzchnie boczne pala w obrębie poszczególnych warstw :

A_sIIa = 0.942*2.05 = 1.93 m²

A_sIIa = 0.942*1.1 = 1.04 m²

A_sIIb = 0.942*2.0 = 1.88 m²

A_sIII = 0.942*x

C. Obliczenie wartości jednostkowych wytrzymałości q^(r) i t_i^(r)

- pod podstawą

q^(r) = 0.87*q_x = 0.87*(2618.84 + 374.12*x) = 2278.39 + 325.48*x

- na pobocznicy

t_IIa^(r) = 0.87*26.02 = 22.63 kPa

t_IIa^(r) = 0.86*37.825 = 32.53 kPa

t_IIb^(r) = 0.86*42.5 = 36.55 kPa

t_III^(r) = 0.87*86.7 = 75.43 kPa.

D. Wyznaczenie długości pala

l_p = 7 + x - 1.45 = (5.55 + x) m.

Ciężar obliczeniowy pala (część pala poniżej z.w.g γ_b' = 24 - 10 = 14 kN/m³)

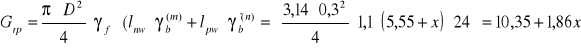
Równanie , z którego wyznaczono x (zagłębienie pala ) :

m*(S_p*q^(r)*A_p+m₁*ΣS_Si*t_i^(r)*A_Si ) ≥ R_r+G_rp

założono wstępnie , że strefy naprężeń nie zachodzą na siebie (m₁ = 1)

0.9*[1.0*(2278.39 + 325.48*x)*0.071+1.0*(0.9*22.63*1.93 + 0.8*32.53*1.04 +0.8*36.55*1.88 + +0.9*75.43*0.942*x)]= 254,80 +78.35x

Po rozwiązaniu metodą prób otrzymano : x = 3.91 m

Obliczona długość pala l_p = 5.55 + 3.91 = 9.46 m

Przyjęto l_p = 9,5 m.

E. Sprawdzenie nośności pala w grupie

Promień podstawy strefy naprężeń

R = (D/2)+Σh_i*tgα_i = (0.3/2)+2,05*0.105+3.1*0.070+0.105*5.35 =0.931

Osiowy rozstaw pali r = 1.83 m.

(r/R) = (1.83/0.931) = 1.97 z tab. 5.4 m₁ = 1

Strefy naprężeń na siebie nie zachodzą , nośność pala jest więc równa nośności pala pojedynczego. Przyjęta długość pala jest zatem wystarczająca.

3. Wymiarowanie ławy

A. Zbrojenie poprzeczne ławy

Obliczeniowa siła rozciągająca zbrojenie :

Z = [R_r*((r/2)+e)]/h_o = [543.824*((0.9/2)+0.05)]/0.6 = 453,18 kN.

Potrzebna ilość zbrojenia

F_a = (Z/R_a) = (453,18 /310000) =0.001461 m² = 14,61 cm².

Przyjęto 10 φ 14 o F_a = 15,4 cm² co 10 cm

B. Zbrojenie podłużne ławy

Ciężar własny ławy , ciężar gruntu nad ławą , ciężar posadzki :

G_r = G_1r + G_2r + G_3r + G_4r = 29.57+3.28+9.18+2.86 = 44.89 kN/m

Ciężar pryzmy trójkątnej muru :

N_r = 1.1*N_n = 1.1*l_o*tg60^o *a+γ_m⁽ⁿ⁾ = 1.1*1.60*1.73 *0.30*18 = 16.44 kN/m

N_r+G_r = 16.44+44.89 = 61.33 kN/m

l = 2*l_o = 2*1.60 = 3.20 m

M₁ = (61.33 *3.20²)/9 = 69.78 kNm

M₂ = (61.33 *3.20²)/14 = 44.86 kNm

M₃ = (61.33 *3.20²)/11 = 57.09 kNm

F_a1 = M/(0.9*h_o*R_a) = 69.78/(0.9*0.6*310*10³) = 4.17*10^-4 m²

F_a1 < F_a^min

F_a^min = b*h_o*μ = 160*60*0.0015 = 14.4 cm²

Przyjęto : 6 φ 18 o F_a = 15,27 cm² rozmieszczonych równomiernie na całej szerokości ławy.

4. Obliczenie osiadania :

Obciążenia charakterystyczne stałe i zmienne długotrwałe :

P_n = 250 kN/m

Charakterystyczny ciężar 1mb ławy :

G_1n = 26.88 kN/m,

Charakterystyczny ciężar posadzki:

G_2n = 2.52 kN/m,

Charakterystyczny ciężar gruntu nasypowego:

z lewej strony G_3n = 7.65 kN/m,

z prawej strony G_4n = 2.38 kN/m

Charakterystyczny ciężar własny jednego pala

G_5n = 9.5*3.14*0.3²*0.25*24 = 16.11 kN/m,

Charakterystyczny ciężar własny jednego pala w obrębie piasków średnich i torfów

G'_5n = 2.45*3.14*0.3²*0.25*24 = 4.15 kN/m,

Siła przypadająca na pal :

Q_nF = (P_n+G_1n+G_2n+G_3n+G_4n)*l_o = (250+26.88+2.52+7.65+2.38)*1.60 = 463,09 kN

Warstwa I, piasek średni, miąższość 2.0 m

E_oI=70000 E_oI=0.8*70000= 56000 kPa

Warstwa II, torf

Warstwa III, glina pylasta zwięzła, miąższość 3.1 m

E_oIII=32500 E_oIII=0.8*32500= 26000 kPa

Warstwa IV, żwir, miąższość 5.35 m

E_oIV=130000 E_oIV=0.8*130000= 104000 kPa

Moduł odkształcenia dla gruntów uwarstwionych wzdłuż pobocznicy pala :

E_o = (56000*2.05+26000*3.1+104000*4.35)/(2.05+3.1+4.35) = 68189 kPa

Moduł odkształcenia dla gruntu poniżej podstawy pala :

E_b = 1.0*130000= 130000 kPa

Osiadanie pojedynczego pala :

s = (Q_n*I_w)/(h*E_o) I_w = I_OK*R_b

(h/D) = 7.05/0.3 = 23.5 (E_b/E_o) = 130000/68189 = 1.9

R_A = 1 (pal pełny)

Dla betonu B20 E_b = E_t = 26*10⁶ kPa

K_a = (E_t/E_o)*R_a = (26*10⁶/68189) = 381.29

z nomogramu 6.1 (skrypt) odczytano I_OK = 3.1 R_b = 0.96

I_w = 3.1*0.96 = 2.98

Osiadanie pojedynczego pala od obciążenia jednostkowego

s₁ = (Q_n*I_w)/(h*E_o) = (0.96*2.98)/(7.05*68189) = 0.60*10^-5 m

Osiadanie pala od siły Q_n = Q_nF+G_5n+Tn (T_n -siła od tarcia ujemnego)

T⁽ⁿ⁾ = 0 kN

Q_n = 463,09 +16,11 = 479,2 kN

s = 6.0*10^-6 * 479,2 = 0.0029 m = 29 mm

Osiadanie pala w grupie składającej się z 4 pali :

s_i = s_1i*Q_ni+Σs_1j*Q_nj*α_ij^o

α_ij^o = α_F^o-F_E*(α_F^o-α_E^o)

Numer pala	D/r	Ka	h/D	αF^o	αE^o	FE	αij^o
2	0.094	381,29	23,5	0.15	0.02	0.02	0.14
3	0.164	381,29	23,5	0.20	0.05	0.02	0.197
4	0.164	381,29	23,5	0.20	0.05	0.02	0.197
5	0.094	381,29	23,5	0.15	0.02	0.02	0.14

Osiadanie dowolnego pala w gruncie nośnym :

s₁ = 2.9*10^-3+0.6*10^-5*479,2*(2*0.14+2*0.197) = 5.6*10^-3 m.

Skrócenie pala w obrębie gruntów nienośnych:

Δs =(Q_nf+0.5*( T⁽ⁿ⁾+ G'_5n )*h/A_p*E_t=

= (463,09 + 0.5*(0+4.15)*2.45)/(3.14*0.3²0.25*26000000) = 0.00062 m = 0.062 cm

Całkowite osiadanie pala:

s_c = s₁ + Δs = 5.6*10^-3 + 0.00062 = 0.0062 m

Obliczoną wartość osiadania należy porównać z wartością wynikającą z analizy stanów granicznych konstrukcji projektowanej budowli , wymagań użytkowych i eksploatacyjnych urządzeń , a także działania połączeń instalacyjnych. Jeżeli obliczone wartości przekraczają wartości dopuszczalne , należy przeprojektować fundament.

---