Pytania na zaliczenie z Metod Symulacyjnych w Fizyce i Technice

1. Na czym polega metoda dynamiki molekularnej? Podac zwiezla, ale celna charakterystyke ogolna. Czym rozni sie ona od metod Monte Carlo?

Def 1 . Metoda dynamiki molekularnej (MD)służy do obliczania trajektorii w przestrzeni fazowej molekuł, z których każda oddzielnie podlega klasycznym równaniom ruchu.

Def 2. Metoda Monte Carlo (MC) polega na przedstawieniu rozwiązania postawionego problemu w paostaci parametru pewnej hipotetycznej populacji i używaniu losowych liczb do tworzenia próbki tej populacji, na podstawie której można dokonać statystycznego oszacowania wartości badanego parametru.

Krótko mówiąc metoda MD wylicza bezpośrednio położenie molekuł (atomów) na podstawie równań ruchu, a metoda MC wykorzystuje narzędzia statystyczne.

2. Co rozumiemy przez "pudlo symulacyjne"? Co to sa i czemu sluza "periodyczne warunki brzegowe"? Optymalny algorytm ich realizacji. Niekonwencjonalne metody budowy ukladow pseudo-nieskonczonych.

„Pudło symulacyjne” - komórka MD, obszar w przestrzeni o stałej gęstości, w którym przeprowadzamy symulacje.(Najczęściej w kształcie sześcianu)

Periodyczne warunki brzegowe - komórka bazowa powtarza się nieskończenie wiele razy. (Istnienie niepotrzebnych ścian w komórce MD spowodowałoby odbijanie się atomów od ich powierzchni co znacząco wpływa na właściwości układu)

A(x)=A(x+nL)

L - długość komórki

Praktycznie rzecz biorąc, jeżeli cząstka przechodzi przez jedną ścianę komórki, to pojawia się ona przy przeciwległej ścianie.

Inne metody układów pseudonieskończonych -

Orthohombic periodic boundaries - zamiast sześcianu prostopadłościan

Parallelpiped periodic boudaries - jak orthohombic tylko między ścianami może być dowolny kąt (przeważnie używany do symulacji kryształów)

Slab boundary conditions - nieskończoność tylko w 2 wymiarach(stosowane do symulowania powierzchni)

3. Jakie cechy powinny miec algorytmy calkowania rownan ruchu w metodach dynamiki molekularnej? Wyprowadzic algorytmy Verleta i "zabiego kroku".

-algorytm powinien być szybki (metody MD wymagają bardzo wielu obliczeń numerycznych) oraz dokładny .

d²x/dt²=F(x1,…,x3n)/m

x(t+h)=x(t)+hdx(t)/dt + h²/2! d²x(t)/dt² + h³/3! d³x(t)/dt³+…

x(t-h)=x(t)-hdx(t)/dt + h²/2! d²x(t)/dt² - h³/3! d³x(t)/dt³+…

x(t+h)=2x(t)-x(t-h)+h²F(t)/m - metoda Verleta

x(t+h)=x(t)+h (dx/dt+ h/2 d²x/dt²) + …

x(t+h)=x(t)+h dx(t+h/2)/dt

dx(t+h/2)/dt=dx/dt +h/2 d²x(t)/dt²

dx(t-h/2)/dt=dx/dt -h/2 d²x(t)/dt²

dx(t+h/2)/dt=dx(t-h/2)/dt+hF(t)/m - metoda „żabiego skoku“

4. Jak sprawdzamy formalna (numeryczna) poprawnosc symulacji dynamiczno-molekularnych? Oszacowac dlugosc kroku czasowego odpowiedniego do realizacji symulacji dynamiczno-molekularnych.

Zjawiska dynamiczno molekularne zachodzą w czasie rzędu pikosekund, dlatego aby uzyskać wiarygodne wyniki symulujemy układy z krokiem czasowym rzędu femtosekund.

5. Na czym polega problem "identyfikacji najblizszych sasiadow"? Opisac metode listy Verleta. Opisac metode cel polaczonych (Hockney'a). Czemu ona sluzy? Podac jej zalety i wady.

Aby oszczędzić moc obliczeniową, możemy wyliczać potencjał tylko do pewnego promienia r_cut, zakładając że potencjał od pozostałych cząstek jest bliski zeru. W tym celu tworzymy listę najbliższych sąsiadów(lista Verleta) dla każdej cząstki w układzie. Należy pamiętać że lista najbliższych sąsiadów może się zmieniać po pewnej ilości kroków czasowych. Dla tego co pewną ilość kroków n, należy uaktualniać listę. Wadą tej metody jest fakt, ze samo stworzenie listy jest czasochłonne(~N²) a przechowywanie zajmuje cenne miejsce na twardych dyskach(~N).

Metoda cel połączonych - podstawową komórkę dzielimy na podkomórki(subcells). W każdym kroku czasowym tworzona jest lista cząsteczek znajdujących się w każdej podkomórce. Aby uzyskać listę najbliższych sąsiadów operujemy na podkomórkach, a nie na samych cząsteczkach. Dzięki temu, że układ podkomórek jest stały i znany metoda ta jest szybsza od metody Verleta(~N). Wadą tej metody jest trudność efektywnego zaimplementowania tej metody na procesorach wektorowych (stosowanych w superkomputerach)

6. Co to sa "poprawki dalekozasiegowe"? Podac przyklady wielkosci fizycznych, dla ktorych konieczne jest uwzglednianie tych poprawek.

Poprawki dalekozasięgowe - poprawki wynikające z odcięcia potencjału w punkcie r_cut

Wielkości fizycze - energia potencjalna i energia całkowita.

7. Omowic metody charakteryzacji uporzadkowania bliskiego zasiegu w materialach symulowanych numerycznie (radialne i katowe funkcje rozkladu, metody geometrii stochastycznej).

Radialna funkcja rozkładu -

8. Omowic metody charakteryzacji uporzadkowania sredniego zasiegu w materialach symulowanych numerycznie (analiza pierscieniowa, analiza wspolnych sasiadow).

Nie wiem

9. Co oznaczaja pojecia "termalizacji" i "probkowania" ukladu w symulacjach dynamiczno-molekularnych? Na czym polega, jak jest realizowane i czemu sluzy w metodach dynamiczno-molekularnych tzw. "skalowanie predkosci"?

termalizacja - zmiana temperatury w celu zrównoważenia układu

próbkowanie - sposób na obliczenie całki(wykorzystywany w metoda stochastycznych)

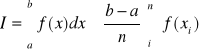
- próbkowanie bezpośrednie

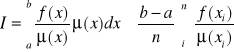
- próbkowanie ważone

Skalowanie prędkości -

1. Scałkuj równania ruchu dla pewnej liczby kroków czasowych

2. Oblicz energię kinetyczną i potencjalną

3. Jeżeli energia nie jest równa energii żądanej, to przeskaluj prędkości

4. Powtarzaj od kroku 1. dopóki układ nie znajdzie się w równowadze.

Stosujemy skalowanie prędkości w celu uzyskania energii cząstek bliskich energiom rządanym.

W praktyce poza doborem algorytmu jest kilka ważnych warunków, których spełnienie jest wymagane dla powodzenia symulacji. Po pierwsze początkowy model może zawierać zdeformowane fragmenty, które podczas symulacji będą podlegać gwałtownej relaksacji, co może zniszczyć lokalną strukturę układu. Dlatego przed symulacją MD konieczne jest zminimalizowanie energii układu. Dodatkowo należy poddać układ procesowi termalizacji, w którym temperatura będzie stopniowo podnoszona, a prędkości początkowe losowane wielokrotnie. W ten sposoób wszystkie ewentualne naprężenia, będą mogły ulec rozprężeniu bez nadawania fragmentom układu dużych prędkości względnych, co mogłoby rozbić lokalną strukturę.

10. Omowic sposob generacji polozen i predkosci poczatkowych w symulacjach dynamiczno-molekularnych.

Lattice start- Układ periodyczny zapewnia odpowiednią odległość między środkami mas(by nie uzyskały gigantycznych energii)

Skew start-Start skośny, brak regularności, ale zapewniona odległość pomiędzy środkami mas. Sposób bardziej zbliżony do rzeczywistości.

Moldy provides two methods of setting up an initial configuration. By default the skew start method of section 2.9.1 is used to place the molecular centres of mass in a regular arrangement which ensures molecular separation. If there is more than one species present, molecules of each are chosen randomly for each site. Molecular orientations are chosen randomly from a uniform distribution. This method has been found to work well for reasonably small or fairly isotropic molecules and it is anticipated that it will be the usual method of starting a simulation of the liquid state. On the other hand, if the constituent molecules are sufficiently large and irregular, or if it is intended to simulate the solid state then the lattice start method will be more appropriate.

rys. skew start
11. Jak w symulacjach dynamiczno-molekularnych obliczamy wspolczynnik dyfuzji? Jaka informacje niesie jego zaleznosc od temperatury?

msd=1/N suma_i^N(r_i(0)-r_i(r))²

D=msd/dt

Im wyższa temperatura tym wyższy współczynnik dyfuzji. Współczynnik dyfuzji niesie informacje czy układ znajduje się w równowadze i jego zależność od temperatury niesie informacje o energii cząstek układu.

12. Omowic metode obliczania oddzialywan kulombowskich w symulacjach dynamiczno-molekularnych (metoda Ewalda). Skad wynikaja "klopoty" z liczeniem sil kulombowskich?

Metoda Ewalda zamienia punktowy rozkład ładunkow w postaci dystrybucji na łatwo-całkowalny rozkład gaussowski.

13. Co to jest model powlokowy (Kochrana i Finchama)? Przy symulacjach jakich zwiazkow koniczne jest jego stosowanie? Czym rozni sie przebieg symulacji z modelem powlokowym oddzialywan od symulacji ukladow izotropowych czastek punktowych?

Modele powłokowe - traktujemy atom jako jądro o ładunku q1 i sferycznej powłoce o ładunku q2. q=q1+q2

Model Kochrana - powłoka jest przytwierdzona na stale do śroka jądra. Powłoka nie ma masy. Cała masa znajduje się w jądrze.

Model Finchama - powłoka przytwierdzona jest sprężynką o stałej k do jądra . Powłoka musi posiadać masę, aby można było obliczyć jej równania ruchu. (Mamy dwa razy więcej ciał).

Wykorzystujemy model powłokowy przy związkach o małej liczbie atomowej, gdzie masa elektronów ma wpływ na ruch molekuły.

Model powłokowy w przeciwieństwie do modelu cząstek punktowych uwzględnia masę i ładunek powłoki

14. Scharakteryzowac symulacje ukladow molekularnych. Co to jest metoda kwaternionowa? Dlaczego jej uzywamy? Podac podobienstwa i roznice symulacji ukladow molekul sztywnych i molekul deformowalnych.

Symulacja układów molekularnych różni się do symulacji cząstek punktowych, tym że zamiast cząstek mamy molekuły i jeżeli chcemy uzyskać wysoką dokładność powinniśmy symulować zjawiska zachodzące wewnątrz tej molekuły

Obrót bryły sztywnej (molekuły) można przedstawić za pomocą kwaternionów o długości 1. Przy pomocy kwaternionów możemy opisać układ mniejszą ilością równań.

Kwaterniony - 4 liczb zespolonych ( 1 rzeczywista i 3 urojone)

Wyznaczamy położenie i prędkości cząsteczek za pomocą tych samych równań, jednak dodatkowo w modelu molekuł deformowalnych uwzględniamy wewnętrzne wibracje molekuły.

15. Na czym polegaja i co naja na celu "metody ukladow skrepowanych wiezami" (constraint system methods)? Podac przyklad termostatu realizowanego ta metoda.

Metoda więzów upraszcza układ równań eliminując zbędne zmienne niezależne. Zmniejszenie ilości stopni swobody przyspiesza obiczenia numeryczne.

Algorytm SHAKE - wytrząsania

-definiuje się pole siłowe, oddziaływania

-liczy się siły

-minimalizacja funkcji wielu zmiennych (relaksacja układu)

16. Na czym polegaja i co naja na celu "metody ukladow rozszerzonych" (extended system methods)? Podac przyklad barostatu i termostatu realizowanych ta metoda.

Polega na rozszerzeniu hamiltonianu o dodatkowe czynniki związane z warunkami fizycznymi ruchu typu ciśnienie, temperatura czy współczynniki tarcia.

Sprzężenie ciśnieniowe Parrinello-Rahmana lub Berendsena

- Termostat Nose-Hoovera

---