Ćwiczenie nr: 11

Badanie właściwości promieniowania gamma za pomocą spektrometru scyntylacyjnego.

1. Wstęp

Jądro atomowe znajdujące się w stanie energetycznym E₁ ,który jest stanem wzbudzonym, może przejść do stanu E₂ z emisją kwantu γ .Jądro może emitować jeden lub więcej kwantów γ o różnych energiach. Mierząc energię kwantów γ emitowanych przez wzbudzone jądra możemy wyznaczyć energie poszczególnych poziomów jądrowych. Do pomiaru energii kwantów γ w ćwiczeniu wykorzystywaliśmy spektrometr scyntylacyjny. Zasadniczą częścią spektrometru jest licznik scyntylacyjny , który składa się z kryształu scyntylacyjnego (NaJ[Tl]) i fotopowielacza. Działanie licznika polega na :

-absorbowaniu energii od promieniowania γ w wyniku wystąpienia zjawiska fotoelektrycznego, rozproszenia comptonowskiego lub tworzenia par elektron-pozyton

- zamianie części energii na energię emitowanych fotonów

- powielaniu fotoelektronów w fotopowielaczu

- posegregowaniu i zliczeniu impulsów w wielokanałowym analizatorze amplitudy.

Efektem pomiaru jest otrzymanie obrazu widma , który został dołączony do sprawozdania.

Aby móc określić energię kwantów γ emitowanych przez dany izotop musimy wyskalować spektrometr (przypisać amplitudom impulsów energie kwantów ) otrzymując prostą skalowania. Następnie mając widmo badanego izotopu z położeń pików , w oparciu o prostą skalowania, wyznaczyć ich energie.

Na podstawie znajomości schematów rozpadu dla poszczególnych pierwiastków doszliśmy do wniosku , że do skalowania spektrometru należy użyć izotopu kobaltu ⁶⁰₂₇Co ze względu na występowanie podczas rozpadu emisji dwóch kwantów γ (wzbudzone jądro niklu emituje dwa kwanty γ o różnych wartościach energii-1.33 MeV oraz 1,17 MeV) co daje nam trzy punkty do wyznaczenia prostej. Poza tym energia kwantów kobaltu jest największa, pozwala to na dokładniejsze wyskalowanie spektometru.

2.Wyznaczenie prostej skalowania

Na podstawie trzech punktów wyznaczamy prostą skalowania przy pomocy programu opartego na metodzie najmniejszej sumy kwadratów. Otrzymaliśmy następującą zależność liniową:

E = a⋅N + b

gdzie: N - numer kanału; E - energia.

a = 4,205E-04 ± 1,402E-06;

b = -5,714E-02 ± 3,603E-03;

czyli ostatecznie:

a=(4,205±0,015)*10^-4 MeV

b=(-5.7±0,4)*10^-2 MeV

Wartość doświadczalna energii dla poszczególnych kanałów wyznaczamy ze wzoru:

E = 4,21E-4⋅ N - 5,7E-2

Błąd wyznaczenia energii obliczamy ze wzoru:

ΔE= aΔN +NΔa + Δb

• błąd wartości N czyli ustawienia kanału przyjmuje równy ±15, ponieważ wykresy są „postrzępione i niesymetryczne” i trudno określić kanał dla maksymalnej energii

4.Wyniki obliczeń

Dla Co

Punkt:	8	7	6	5	4	3	2	1
Nr kanału:	211	636	2289	2400	2520	2912	3127	3303
E [MeV]	0,03	0,21	0,91	0,95	1,01	1,17	1,26	1,33
ΔE*10^-3 [MeV]	11	12	14	14	15	15	15	16

Dla Cs

Punkt:	6	5	4	3	2	1
Nr kanału:	216	551	1175	1240	1325	1690
Energia [MeV]	0,03	0,17	0,44	0,46	0,50	0,65
ΔE*10^-3 [MeV]	11	13	13	13	13	13

Dla Na

Punkt:	13	12	11	10	9	8	7	6	5	4	3	2	1
Nr kanału:	222	535	695	810	887	963	1236	1309	1374	2539	2655	2750	3166
Energia [MeV]	0,04	0,17	0,24	0,28	0,32	0,35	0,46	0,49	0,52	1,01	1,06	1,10	1,27
ΔE*10^-3 [MeV]	11	12	12	12	12	12	13	13	13	15	15	15	16

5. Interpretacja otrzymanych widm

Kwanty γ nie mogą bezpośrednio wytwarzać impulsów wyjściowych w scyntylatorze.

Przekazują one energię elektronom , a te dopiero wzbudzają atomy scyntylatora.

Przekazanie energii elektronom może zajść w jednym z trzech zjawisk :

-zjawisku fotoelektrycznym

-zjawisku Comptona

-zjawisku tworzenia pary elektron-pozyton

W zjawisku fotoelektrycznym kwant γ zanika po oddaniu energii elektronowi. Miejsce wybitego elektronu zajmuje elektron z wyższych powłok , emitowany przy tym jest kwant energii. Kwant ten oddaje całą swoją energię scyntylatorowi. Efektem zjawiska fotoelektrycznego jest powstanie charakterystycznych impulsów zwanych fotopikami. W zjawisku Comptona kwanty γ rozpraszane są na swobodnych elektronach. Wskutek rozpraszania comptonowskiego elektrony uzyskują pewną energię_.

a) kobalt ⁶⁰₂₇Co

Obserwując widmo energetyczne kobaltu ( załączony wydruk komputerowy ) widzimy dwa charakterystyczne piki-1 i 3. Odpowiadają im różne wartości energii odpowiednio 1,33 [MeV] oraz 1,17 [MeV]. Te poziomy energetyczne powstały wskutek rozkładu atomów C_o na N_i^* i N_i. Widmo od punktu 4 w lewo powstało w wyniku zjawiska Comptona. Polega ono na sprężystym zderzeniu fotonu ze swobodnym elektronem. W takim to zderzeniu zgodnie z zasadami zachowania energii i pędu foton przekazuje tylko część swej energii i pędu. Maksimum
daje się wyznaczyć z wcześniej wymienionych zasad.
,uzyskujemy to zakładając:

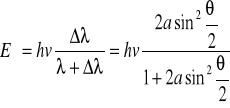
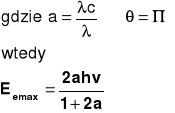
dla kobaltu jest to E_emax=0,96 MeV dla Eγ=1,17. Punkty 4,5,6 tworzą prostą tzw. krawędź Comptonowską. Określa ona maksymalne wartości energii elektronu uzyskane wskutek efektu Comptona. Pik 7 powstał w wyniku zderzenia fotonu z elektronem. Pik 8 powstaje wskutek wybijania elektronów z powłoki K. Jego miejsce zajmuje elektron z wyższej powłoki. Towarzyszy temu zjawisku energia, która świadczy o tym iż jest to promieniowanie Rentgenowskie.

Obserwując widmo energetyczne można zauważyć, że całość widma jest sumą widma ciągłego oraz pików odpowiadających pewnym charakterystycznym wartościom energii.

b) Interpretacja widma cezu ¹³⁷₅₅Cs

Pierwszy fotopik powstał w wyniku efektu fotoelektrycznego. Cez w wyniku rozpadu przechodzi w Bar o stanie wzbudzonym. A następnie Ba^* przechodzi do stanu podstawowego emitując kwant γ o energii 0,66 [MeV]. Kwanty γ przekazały energię elektronom na jednaj z powłok. Elektrony te powodując jonizację powodowały pośrednio zliczanie impulsów przez spektrometr. Punkty 2-3-4 tworzą krawędź Comptonowską. Określa ona maksymalne wartości energii elektronu uzyskane na skutek efektu Comptona. Następnie można zauważyć rozmycie krawędzi Comptonowskiej. Zjawisko to może wynikać z tego, iż rozproszone elektrony mogą wywoływać później zjawisko fotoelektryczne. Punkt 3 to granica efektu Comptona czyli maksymalna energia, jaką mogą otrzymać elektrony od kwantów γ. Punkt 5 to efekt fotoelektryczny. Po zderzeniu się fotonu o energii 0,65 MeV z elektronem i przekazaniu mu części energii następuje kolejne zderzenie się tego fotonu już o energii 0,17 MeV. Pik 6 to również efekt fotoelektryczny w wyniku, którego po zajęciu przez elektron miejsca po wybitym przez foton elektronie, następuje wydzielenie się nadmiaru energii, która wskazuje na to, iż jest to promieniowanie X.

c) Interpretacja widma sodu ²²₁₁Na

Rozpad sodu może zajść w dwojaki sposób:

• Bezpośrednio na neon bez wydzielania kwantu γ

• Częściowy rozpad, a następnie wydzielenie kwantów γ.

Punkt 1 powstał w wyniku zjawiska fotoelektrycznego, w którym cała energia kwantu przekazana jest elektronowi (posiada on energie równą 1,27 [MeV]). Można zauważyć dwie krawędzie Comptonowskie, tworzone przez punkty 2-3-4, 8-9-10. Krawędź 2-3-4 powstała w wyniku rozproszenia się kwantów γ ( uzyskanych w efekcie Comptona) na elektronach. Pochylenie tej krawędzi spowodowane jest wielokrotnym rozpraszaniem Comptona. Druga krawędź (punkty 8-9-10) ma te same znaczenie, tylko powstała w wyniku efektu fotoelektrycznego. Prosta utworzona z punktów 10-11-12 odpowiada zjawisku Comptona. Foto pik 13 to wyemitowanie fali elektromagnetycznej na skutek oddania nadmiernej energii przez elektron, zajmujący wolne miejsce w powłoce o niższej energii - z porównania energii można wywnioskować, iż jest to promieniowanie X.

---