Leszek Mróz Gr. 25 Zespół 5

Ćwiczenie 35

Badanie pętli histerezy magnetycznej ferromagnetyków i ferrytów przy użyciu oscyloskopu.

1. Wiadomości wstępne.

Podczas ćwiczenia zajmowaliśmy się badaniem pętli histerezy dla różnych materiałów. Pomiarów dokonywaliśmy przy użyciu oscyloskopu. Urządzenie to składało się z torsoidu na który nawinięte są dwa uzwojenia: pierwotne i wtórne. Uzwojenie pierwotne, zasilane prądem z zasilacza, wytwarza w uzwojeniu pole H, które indukuje prąd płynący w obwodzie wtórnym. Obwód jest tak zbudowany, aby sygnał napięciowy na płytkach uzwojenia pierwotnego (X) był proporcjonalny do natężenia H, a sygnał na płytkach uzwojenia wtórnego (Y) był proporcjonalny do indukcji pola magnetycznego B (co zapewnia układ całkujący składający się z kondensatora i opornika). Na początku ćwiczenia wsuwaliśmy w torsoid rdzenie wykonane z różnych materiałów i porównywaliśmy jakościowo powstałe w wyniku tego pętle histerezy. Następnie rdzenie te zostały zastąpione kolejno dwoma rdzeniami torsoidalnymi, dla których przeprowadzilismy szczegółowe pomiary. Na koniec ćwiczenia zajęliśmy się poszukiwaniem temperatury Curie dla pewnego materiału, poprzez wsuwanie wykonanego z niego rdzenia torsoidalengo do stopniowo nagrzewanego oleju.

2. Pomiary jakościowe.

Na początku ćwiczenia obserwowaliśmy pętle histerezy od wykonanych z różnych materiałów walcowatych rdzeni, wsuwanych w torsoid oscyloskopu. Obserwacjom poddawane były pętle pochodzące od czterech rdzeni. Materiał z którego wykonany był pierwszy z nich, można uznać za miękki. Jego pętla była dość wąska, chociaż jej końce były mocno wydłużone. Dla rdzenia drugiego nie zaobserwowaliśmy pętli histerezy, czyli musieliśmy mieć do czynienia z paramagnetykiem. Rdzeń trzeci i czwarty były prawdopodobnie wykonane z tego samego materiału. Ich pętle histerezy były dwa razy szersze niż w przypadku pierwszego rdzenia. Uznaliśmy, że ten materiał można określić jako twardy.

3. Pomiary dla rdzeni torsoidalnych.

Dwa rdzenie torsoidalne przebadane za pomocą oscyloskopu przedstawia, oraz wartości charakteryzujące ich pętle histerezy przedstawia poniższa tabela.

Tabela 1:

Materiał	Pole przekroju	L. zwojów Uzwoejnia pierowotnego	L. zwojów Uzwoejnia wtórnego	Długość uzwojenia	I skuteczne w uzwojeniu pierowotnym	Pola koercji	xmax	Ind. resztkowa	Ind. nasycenia [V]
	S+ΔS [m^2]	N1	N2	l+Δl [m]	Isk+ΔIsk [A]	xc+Δxc [mm]	[mm]	Ur+ΔUr [V]	Us+ΔUs [V]
ferryt	0,0001± 0,000002	130	1200	0,100± 0,001	2,5±0,11	20±1	44±1	0,21±0,02	0,30±0,02
permalej	0,000096 ±0,000004	250	600	0.080± 0,001	0,0200±0,0011	16±1	45±1	0,10±0,02	0,12±0,02

Błąd natężenia skutecznego został policzony ze wzoru:

ΔI_sk=(klasa)*(zakres)/100 + (zakres)/(liczba działek),

ponieważ błąd będzie sumą błędów wynikających z klasy urządzenia i możliwości odczytu.

ΔI_skF=2*3/100+3/60=0,06+0,05=0,11A

ΔI_skP=2*0,03/100+0,03/60=0,0006+0,0005=0,0011A

Następnie oba rdzenie zasililiśmy małym prądem magnesującym tak, aby na ekranie widoczna była prosta (taki przypadek uzyskaliśmy przy badaniu permaleju) lub wydłużona elipsa (w przypadku ferrytu). Stopniowo zwiększaliśmy natężenie prąd, za każdym razem notując I_sk oraz U_c.

Nr pomiaru	materiał	Isk ± ΔIsk [A]	Imax ± ΔImax [A]	Uc ± ΔUc [V]	H±ΔH [A/m]	B ± ΔB	μ ± Δμ
1	permaloj	0,00033±0,00037	0,00047±0,00053	0,06±0,02	1,3±1,5	0,21±0,12	130000±230000
2	permaloj	0,00033±0,00037	0,00047±0,00053	0,07±0,02	1,3±1,5	0,24±0,13	150000±250000
3	permaloj	0,00042±0,00037	0,00059±0,00053	0,08±0,02	1,7±1,5	0,28±0,14	130000±190000
4	permaloj	0,00050±0,00037	0,00071±0,00053	0,10±0,02	2,0±1,5	0,35±0,16	140000±170000
1	ferryt	0,135±0,011	0,184±0,016	0,04±0,02	248±21	0,07±0,05	220±180
2	ferryt	0,095±0,011	0,134±0,016	0,03±0,02	175±21	0,050±0,045	230±240
3	ferryt	0,070±0,011	0,099±0,016	0,02±0,02	129±21	0,033±0,041	200±300
4	ferryt	0,055±0,011	0,078±0,016	0,01±0,02	101±21	0,02±0,04	160±350

Tabela 2:

Błąd I_sk będzie wynosił obliczając analogicznie jak poprzednio:

ΔI_skF=2*0,3/100+0,3/60=0,006+0,005=0,011

ΔI_skP=2*0,01/100+0,01/60=0,000366667 ; ΔI_skP=0,00037;

Do wypełnienia pozostałych kolumn tabeli wykorzystano wzory:

I_max= I_sk√2, ΔI_max=Δ I_sk√2

H=(√2I_sk*x_max*N₁)/(l*x_max)= (I_max*N₁)/l

Ten wzór może być również wykorzystany do obliczenia H_c, jeżeli x_max w liczniku zostanie zastąpiony x_c.

ΔH=(√2*N₁)/lΔI_sk+ (√2I_sk*N₁)/(l²)Δl

ΔH_1p =1,486531 + 6,02648 * 10^-5 = 1,486591566 [A/m]

ΔH_2p =1,486531 + 6,02648 * 10^-5= 1,486591566 [A/m]

ΔH_3p =1,486531 + 7,67006 * 10^-5= 1,486608002 [A/m]

ΔH_4p =1,486531 + 9,13103 * 10^-5 = 1,486622612 [A/m]

ΔH_1f =20,223 + 0,019091883 = 20,24234583 [A/m]

ΔH_2f =20,223 + 0,013435029 = 20,23668897 [A/m]

ΔH_3f =20,223 + 0,009899495 =20,23315344 [A/m]

ΔH_4f =20,223 + 0,007778175 = 20,23103212 [A/m]

Wartości tych błędów zostały policzone za pomocą kompletnego algorytmu w programie EXCEL. W tabeli zostały zamieszczone już ostateczne (zaokrąglone) wyniki.

B=URC/N₂S (z tego wzoru można również wyliczyć B_s i B_r)

R=100kΩ=100 000 Ω-rezystancja opornika układu całkującego,

C=2μF=2*10^-6F-pojermność kondensatora układu całkującego,

ΔB=RC/ N₂S ΔU+URC/ N₂S² ΔS+ UC/ N₂S ΔR+UR/ N₂S ΔC

ΔB1p=	0,069444444 +	0,008681 +	0,020833 +	0,020833 =	0,119792
ΔB2p=	0,069444444 +	0,010127 +	0,024306 +	0,024306 =	0,128183
ΔB3p=	0,069444444 +	0,011574 +	0,027778 +	0,027778 =	0,136574
ΔB4p=	0,069444444+	0,014468 +	0,034722 +	0,034722 =	0,153356
ΔB1f=	0,033333333 +	0,001333 +	0,006667 +	0,006667 =	0,048000
ΔB1f=	0,033333333 +	0,001000 +	0,005000 +	0,005000 =	0,044333
ΔB2f=	0,033333333 +	0,000667 +	0,003333 +	0,003333 =	0,040667
ΔB3f=	0,033333333 +	0,000333 +	0,001667 +	0,001667 =	0,037000
ΔB4f=	0,069444444 +	0,008681 +	0,020833 +	0,020833 =	0,119792

Jako ΔR i ΔC przyjeliśmy 10% wartości R i C.

μ=B/μ_oH

μ_o=4π*10^-7 [N/A²]

Δμ1p=	73456,12757 +	148324,8730 =	221781,0006
Δμ2p=	79577,47154 +	169514,1405 =	249091,6121
Δμ3p=	65534,38832 +	115648,9206 =	181183,3089
Δμ4p=	63661,97723 +	104445,4314 =	168107,4086
Δμ1f=	160,4384507 +	19,01971956 =	179,4581702
Δμ2f=	204,6277839 +	27,28370453 =	231,9114885
Δμ3f=	252,9206460 +	33,13934726 =	286,0599932
Δμ4f=	315,1583031 +	32,76398201 =	347,9222851

Δμ= 1/(H*μ₀)  ΔB + B/(H²*μ₀)  ΔH

Korzystając z tabeli 1 możemy obliczyć B_s - indukcję nasycenia, B_r - indukcja resztkowa,

H_c - natężenie pola koercji oraz błędy tych wielkości. Wzory na H i B zostały podane wcześniej, wzory na niepewności są przedstawione poniżej.

ΔB_s=RC/ N₂S ΔU_s+U_sRC/ N₂S² ΔS+ U_sC/ N₂S ΔR+U_sR/ N₂S ΔC

ΔBsp=	0,069444444 +	0,041666667 +	0,041666667 +	0,017361111 =	0,170138889
ΔBsf=	0,033333333 +	0,046666667 +	0,046666667 +	0,009333333 =	0,136

ΔB_r=RC/ N₂S ΔU_r+U_rRC/ N₂S² ΔS+ U_rC/ N₂S ΔR+U_rR/ N₂S ΔC

ΔBrp=	0,069444444 +	0,034722 +	0,034722 +	0,014467593 =	0,15335648
ΔBrf=	0,033333333 +	0,033333 +	0,033333 +	0,006666667 =	0,10666667

ΔH_c=(√2*x_c *N1)/(l* x_max) ΔI_sk+ (√2*x_c N1)/(l²* x_max) Δl+(√2*N1)/(l* x_max) Δ x_c+(√2*x_c *N1)/(l* x_max²) Δ x_max

ΔHcp=	196,4186 +	47,68426 +	209,8107 +	93,24921 =	547,1627408
ΔHcf=	0,735391 +	0,133707 +	0,835672 +	0,303881 =	2,008650767

Tabela 3:

Badany materiał	Bs±ΔBs [T]	Br±ΔBr [T]	Hc±ΔHc [A/m]
permaloj	0,42±0,18	0,35±0,16	4200±550
ferryt	0,47±0,14	0,33±0,11	13,4±2,1

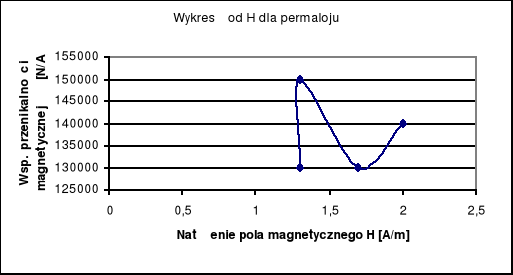
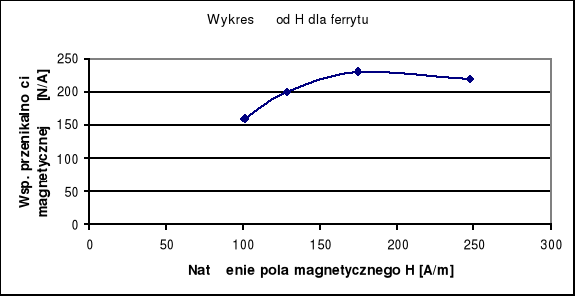
4. Wykresy współczynnika przenikalności magnetycznej badanego materiału

od natężenia pola magnetycznego.

5. Badanie temperatury Curie.

W celu zmierzenia wartości temperatury Curie materiału ferromagnetycznego, podłączyliśmy do oscyloskopu wykonany z tego materiału torsoidalny rdzeń, zanurzony w oleju. Dopóki olej był w temperaturze pokojowej, obserwowaliśmy na wyświetlaczu oscyloskopu wyraźną pętlę histerezy. Kiedy zaczęliśmy podgrzewać olej, obraz przez pewien czas nie uległ zmianie, jednak kiedy podłączony do układu miernik temperatury wskazał 63^o, pętla histerezy bardzo szybko zanikła. Oznaczało to, że na skutek drgań termicznych, badany ferromagnetyk utracił budowę domenową i przeszedł w paraelektryk. Temperaturę, w której zachodzi to zjawisko nazywamy temperaturą Curie. Po wyłączeniu grzałki podgrzewającej olej i wyjęciu rdzenia, pętla histerezy nie pojawiła się od razu. Materiał powrócił do budowy domenowej dopiero w temperaturze 26^o, o czym świadczyło ponowne pojawienie się w tej temperaturze obrazu pętli histerezy na ekranie oscyloskopu.

6. Wnioski.

Badane podczas ćwiczenia rdzenie różnią się między sobą. Fermaloj, jako materiał twardszy jest zdecydowanie lepszy do wykonania magnesu trwałego. O jego twardości świadczy np. duża wartość pola koercji, o dwa rzędy wyższa niż w przypadku ferrytu. Trudno wyciągnąć jakieś głębsze wnioski z wykonanych na podstawie pomiarów obliczeń. Główną przyczyną takiego stanu rzeczy są występujące w wielu przypadkach niepokojąco duże wartości błędów liczonych wielkości. Były one szacowane metodą różniczki zupełnej. Wykorzystywane wzory były dość skomplikowane, co zwiększa prawdopodobieństwo popełnienia pomyłki podczas obliczeń. O tym, że musiał zostać popełniony jakiś błąd nadmierny, czy to podczas pomiarów czy też podczas liczenia, świadczą wykresy μ(H). O ile wykres dla ferrytu jest zbliżony do fragmentu linii teoretycznej (wartość przenikalności dla pewnych H rośnie, lecz od pewnej wartości zaczyna maleć), to wykres dla permaloju nie wydaje się mieć niestety żadnego sensu fizycznego. Przyjmując , że wykonane obliczanie są wystarczające do porównania obu materiałów, można stwierdzić, że właściwości magnetyczne obu materiałów są różne. Ich współczynniki przenikalności magnetycznej różnią się aż o kilka rzędów, niezależnie od natężenia pola magnetycznego. Potwierdzają to różne obrazy ich pętli histerezy. Pętla permaloju jest zarówno szersza jak i dłuższa niż ta pochodząca od ferrytu.

3

---