Wstęp

Celem ćwiczenia było wykonanie pomiarów widma promieni gamma o znanych energiach kwantów gamma za pomocą licznika scyntylacyjnego (Schemat 1). Na powstałych wykresach rozkładu energii należało odnaleźć miejsca charakterystyczne tj. krawędź Comptona, fotoniki czy maksimum rozproszenia wstecznego.

Promieniowanie gamma to wysokoenergetyczna forma promieniowania elektromagnetycznego. Promieniowanie to powstaje w wyniku przemian jądrowych. W związku ze zmianą poziomu energetycznego generowany jest foton lub kilka fotonów o określonej energii. Promieniowanie to jest monoenergetycznym promieniowaniem jonizującym.

Oddziaływanie promieni gamma z materią:

Rozróżniamy 3 zjawiska w którym promieniowanie jest w stanie przekazać swoją energię elektronom. Są nimi: efekt fotoelektryczny, efekt Comptona i efekt tworzenia par. Z tym, że energia przekazywana elektronom może być całkowita lub częściowa. Zasadę funkcjonowania poszczególnych efektów opisałem w sprawdzianie wiadomości z przygotowania w trakcie zajęć.

Układ pomiarowy

Schemat 1

Spektrometr scyntylacyjny składa się z licznika scyntylacyjnego (kryształ scyntylacyjny + fotopowielacz), wzmacniacza liniowego oraz wielokanałowego analizatora amplitudy.

Licznik scyntylacyjny to najważniejszy element spektrometru. Składa on się z kryształu scyntylacyjnego ( w naszym przypadku nieorganiczny jodek sodu aktywowanego talem). Kryształ ten sprzężony jest optycznie z fotopowielaczem, który składa się z fotokatody działającej w obecności silnego pola elektromagnetycznego. Sygnał wychodzący z licznika jako sygnał elektryczny przekazywany jest do wzmacniacza liniowego, a stamtąd do wielokanałowego analizatora amplitudy. Tam sygnał analizowany jest pod względem amplitud i segregowany w odpowiednich kanałach w prostej zależności: Im większy impuls tym większy kanał.

Przebieg wykonania ćwiczenia.

Pierwszą czynnością którą należało wykonać było otrzymanie wartości energii teoretycznych z wykresów rozpadu pierwiastków promieniotwórczych: ¹³⁷Cs, ²²Na, ⁶⁰Co. Kolejnym etapem było badanie odpowiednich próbek przez odpowiednio długi okres, tak by dokładność pomiaru była wystarczająca. Po uzyskaniu wykresów należało rozpoznać rodzaj próbki i wyznaczyć punkty charakterystyczne. Z części wyznaczonych punktów wyznaczyć należało prostą kalibracyjną. Następnie dla punktów charakterystycznych za pomocą prostej kalibracyjnej wyznaczyć należało wartości energii.

Opracowanie wyników

1. Wyznaczanie teoretycznych wartości energii

Wyznaczanie teoretycznych wartości energii Comptona otrzymamy posługująć się wzorem:

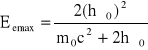
W którym

hν₀ -energia fotonu

m₀c₂ -energia spoczynkowa elektronu i wynosi 0,51 [MeV]

Natomiast piki rozproszenia wstecznego wyznaczać będziemy za pomocą wzoru:

h = h₀ - E_{e max}

• Cez ¹³⁷Cs

¹³⁷₅₅Cs → ¹³⁷₅₆Ba + ⁰_-1B

¹³⁷₅₆Ba* → ¹³⁷₅₆Ba + γ

Pik absorbcji całkowitej - 0,66 [MeV]

Krawędź Comptona

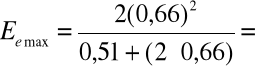
0,476 [MeV]

Maksimum rozproszenia wstecznego- 0,66-0,476= 0,18 [MeV]

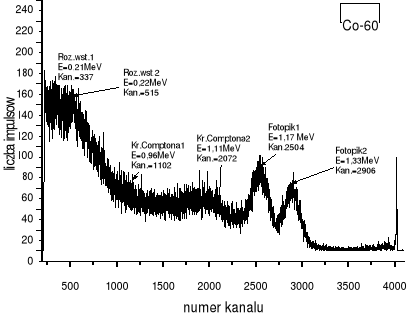
• Sód ²²Na

²²₁₁Na → ²²₁₀Ne* + ⁰₊₁B

²²₁₀Ne* → ²²₁₀Ne + γ

Pik absorpcji całkowitej- 1,28 [MeV]

Krawędź Comptona

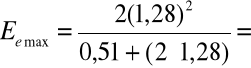
1,067 [MeV];

Pik rozproszenia wstecznego- 1,28-1,067=0,21 [MeV]

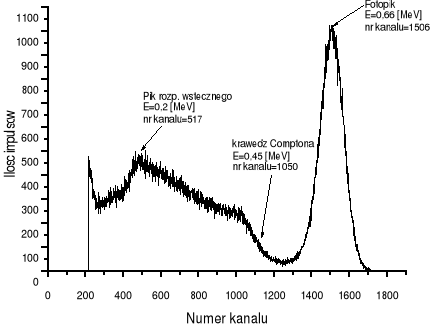
• Kobalt ⁶⁰Co

⁶⁰₂₇Co → ⁶⁰₂₈Ni* + ⁰_-1B

⁶⁰₂₈Ni* → ⁶⁰₂₈Ni* + γ₁

⁶⁰₂₈Ni* → ⁶⁰₂₈Ni + γ₂

Pik absorpcji całkowitej 1- 2,5[MeV]

Pik absorpcji całkowitej 2- 1,33 [MeV]

Krawędzie Comptona 1 i 2

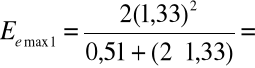
1,12 [MeV]

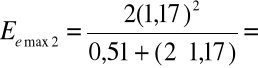
0,96 [MeV]

Maksima rozproszenia wstecznego dla E_{e max1} - 2,5-1,12= 1,38 [MeV]

Maksima rozproszenia wstecznego dla E_{e max2} - 1,33-0,96=0,37 [MeV]

2. Wyniki badania

• ¹³⁷Cs

Punkt	Energia teoretyczna [MeV]	Energia doświadczalna (z prosta kalibracyjnej) [MeV]	ΔE
fotopik	0,66	0,67	0,03
Krawędź Comptona	0,48	0,45	0,02
Maksimum rozproszenia wstecznego	0,18	0,2	0,02

• Kobalt ⁶⁰Co

Punkt	Energia teoretyczna [MeV]	Energia doświadczalna (prosta skalowania) [MeV]	ΔE
fotopik 1	1,17	1,16	0,03
fotopik 2	1,33	1,34	0,04
krawędź comptonowska 1	1,12	0,48	0,02
krawędź comptonowska 2	0,96	0,94	0,03
pik roz. wstecznego 1	0,21	0,11	0,02
pik rozp. wstecznego 2	0,22	0,2	0,02

• Sód ²²Na

Opis	Energia teoretyczna [MeV]	Energia doświadczalna (prosta skalowania) [MeV]
Fotonik	1,28	1,26	0,04
krawędź Comptona	1,07	1,12	0,035
Pik rozp. wstecznego	0,21	-	0,02
Fotopik (anih.)	0,51	0,33	0,02
Krawędź Comptona (anih.)	0,34	0,18	0,02
pik roz. wstecznego (anih.)	0,17	-	0,02

Wartości dla sodu zamieszczone są na głównej stronie sprawozdania

• Prosta kalibracyjna

Do wyliczenia prostej kalibracyjnej pobrane zostały 4 punkty charakterystyczne z 3 powyższych wykresów.

Są nimi:

Punkt	Wartość teoretyczna [MeV]	Numer kanału
Pik absorbcji całkowitej 1 ^66Co	1,33	2906
Pik absorbcji całkowitej 2 ^66Co	1,17	2540
Pik absorbcji całkowitej ^137Cs	0,66	1506
pik anih. absorbcji całkowitej ^22Na	0,51	1159

Z wyznaczonych kanałów i wartości teoretycznych energii w tych miejscach stworzony został wykres. Po przyrównaniu punktów do prostej otrzymaliśmy prostą kalibracyjną w funkcji

Y[MeV]=0,000475567*X[numer kanału]-0,04683

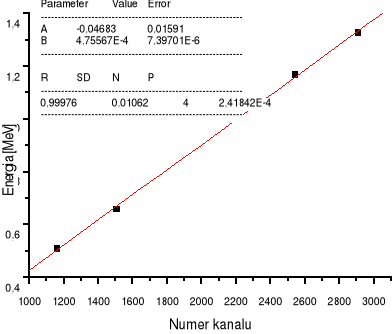
• Wyznaczanie błędów

Błąd wyznaczamy z prostej kalibracyjnej za pomocą różniczki zupełnej:

Y=B*X[numer kanału]-A

Gdzie A=-0,4683 ΔA=0,01591

B=0,000475567 ΔB=0,00000739701

Błąd pomiaru energii wynosi:

ΔE =X*ΔB+ΔA

Wnioski

Wyniki badań potwierdzają założenia. Wielkości doświadczalne zgadzają się w granicy błędu poza jednostkowymi wielkościami np. dla kobaltu ,gdzie krawędzie Comptona prawdopodobnie pokrywają się ze sobą. Brak doświadczenia w czytaniu wykresów sprawił, że pod uwagę wzięliśmy dodatkowy punkt o wartości 0,48 [MeV]. Wykres dla sodu przedstawia specyficzną sytuacje jaka ma miejsce w krysztale scyntylacyjnym. Jeśli energia kwantu γ jest większa od energii spoczynkowej elektronu i pozytonu (czyli od 2m₀c²=1,02[MeV]) to nadmiar energii kwantu przekazywana jest w formie energii kinetycznej na parę pozyton-elektron. Para ta najpierw odda swą energię licznikowi a następnie pozyton, którego żywotność jest bardzo krótka ulegnie anihilacji z jednym z elektronów scyntylatora. Takim sposobem wytworzone zostaną 2 kwanty o energii 0,51[MeV] i także przekazana do licznika. Dzięki temu zjawisku na wykresie zarysowują się dodatkowe wzniesienia wywołane przez zjawisko anihilacji pozytonu.

- 6 -

---