PRZEDMIOT KINEMATYKI I DYNAMIKI UKŁADÓW:

a) Kinematyka

czasoprzestrzeń Galileusza R x R³

R_­­³

X={x₁,x_2,x₃}

Y={y_1,y_2,y₃}

Ruch punktu materialnego jest to przekształcenie czasu w przestrzeń :

X:R→R³ (I ⊂ R x:I→R³ ) I - interwał

Trajektoria funkcja czasu podająca położenie punktu w każdej chwili

1. ciągła!!!!!!!!!

2. odpowiednio gładka

miara długości

TRAJEKTORIA PUNKTU MATERIALNEGO. TRÓJŚCIAN FRENETA.

X(t) = [x₁(t), x₂(t), x₃(t)]

( kierunek predkosci )

(dlugosc)

krzywiyna trajektorii ruchu

wektor binormalny

krzywizna odzwierciedla nieprostoliniowosc trajektorii

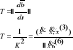
Skrecenie odzwierciedla nieplaskosc trajektorii

W geometrii różniczkowej trójścian Frèneta służy do badania własności krzywych przestrzennych

Równania dynamiki układu z ograniczeniami. Zasada D'Alemberta.

Kinematyka układu robotycznego podlegającego niezależnym ograniczeniom fazowym typu Pfaffa

jest zdefiniowana za pomocą układu sterowania postaci
. Załóżmy, że układ nie podlega ograniczeniom konfiguracyjnym.

. Wektor u reprezentuje część składowych wektora prędkości

Różniczkując
względem czasu otrzymujemy:
. Z zasady D'Alemberta

(siły uogólnione F zapewniające spełnienie ograniczeń fazowych nie wykonują pracy na dopuszczalnych przemieszczeniach) wynika,

że
oraz, że (dla λ∈R^l)
⇒
. Z zależności
,

zakładając, że F=T+u otrzymujemy
.

Mnożąc obie strony równania przez G^T(q) otrzymujemy:

.

Podstawiając za
oraz za

otrzymujemy równania dynamiki układu nieholonomicznego postaci:

PĘD. MOMENT PĘDU I ENERGIA UKŁADU PUNKTÓW MATERIALNYCH

1. Pęd punktu
   

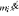
Pęd układu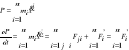

Prędkość zmiany pędu ukłądu jest równa wypadkowej sił zewnętrznych działających na układ. Jeżeli jest równa 0, to P=const.

2. Moment pędu(kręt)
   

Moment układu

Prędkość zmiany momentu pędu układu równa się wypadkowemu momentowi sił zewnętrznych działających na układ. Jeśli jest równa 0, to M=const.

3. Energia kinetyczna:
   

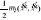
Energia układu

Prędkość zmiany energii kinetycznej układu, jest równa sumie wszystkich mocy układu.

4. Energia potencjalna V(x)

Siła F_i jest potencjalna, jeżeli

5. Energia całkowita E=K+V

b

t

n

s

---