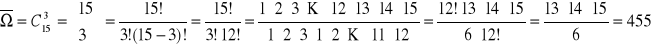
Zadania dotyczące wykorzystania kombinatoryki do obliczania prawdopodobieństwa

Zadanie 1

Z grupy składającej się z 10 kobiet i 5 mężczyzn wybrano w sposób losowy 3 - osobową delegację. Jakie jest prawdopodobieństwo, że w skład delegacji wchodzą i mężczyźni i kobiety?

Rozwiązanie

Do obliczenia prawdopodobieństwa metoda klasyczną musimy wyznaczyć przestrzeń zdarzeń elementarnych

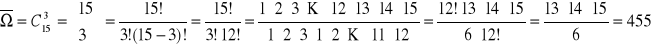
A - zdarzenie polegające na wylosowaniu 3 - osobowej delegacji, w skład której wchodzą i kobiety i mężczyźni.

A₁ - zdarzenie polegające na wylosowaniu 3 - osobowej delegacji, w skład której wchodzi jedna kobieta i dwaj mężczyźni.

A₂ - zdarzenie polegające na wylosowaniu 3 - osobowej delegacji, w skład której wchodzą dwie kobiety i jeden mężczyzna.

A = A₁ ∪A₂

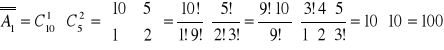
wybór wybór 2 z 5 mężczyzn

1 z 10 kobiet

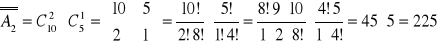
wybór wybór 1 z 5 mężczyzn

2 z 10 kobiet

P(A) =

P(A) =

Odp. Prawdopodobieństwo wylosowania 3 - osobowej delegacji, w skład której wchodzą i kobiety i mężczyźni wynosi 0.71.

Zadanie 2

Rzucamy sześcienną kostką. Jakie jest prawdopodobieństwo, że liczba oczek będzie większa od 5?

Rozwiązanie

Zbiór zdarzeń elementarnych Ω = {1, 2, 3, 4, 5, 6}, zatem liczba możliwych zdarzeń
= 6. Zbiór zdarzeń sprzyjających A = {6}, liczba zdarzeń sprzyjających
= 1. Prawdopodobieństwo zajścia zdarzenia wynosi:

Zadanie 3

Dyrektor pewnego banku przeznaczył na pomieszczenia biurowe dla swoich pracowników 40 pokoi ponumerowanych kolejno od 101 do 140. Poniżej, zestawiono jaki procent liczby pokoi stanowią pokoje jedno, dwu, trzy i czteroosobowe:

Liczba pracowników w pokoju	1	2	3	4
Liczba pokoi	40%	25%	20%	15%

Dyrektor wylosuje numery trzech pokoi, w których zostaną zainstalowane kamery przemysłowe.

Oblicz prawdopodobieństwa zdarzeń:

A - kontrolą objętych zostanie 10 pracowników;

B - w każdym kontrolowanym pokoju pracuje więcej niż jedna osoba personelu;

C - kontroli zostanie poddane co najmniej 5 osób.

Rozwiązanie

Obliczmy liczbę pokoi jedno, dwu, trzy i czteroosobowych.

40% z 40 = 16

25% z 40 = 10

20% z 40 = 8

15% z 40 = 6

 

Obliczamy liczbę wszystkich wyników losowania 3 pokoi z 40 (korzystamy z kombinacji)

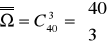
=9880

a)

Obliczmy liczbę wszystkich wyników sprzyjających zdarzeniu

A - kontrolą objętych zostanie 10 pracowników (wylosowane zostaną: 1 pokój dwuosobowy i 2 pokoje czteroosobowe lub 2 pokoje trzyosobowe i jeden pokój czteroosobowy).

Ponieważ wszystkie wyniki są jednakowe prawdopodobne, więc prawdopodobieństwo:

P(A) =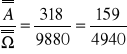

b)

Obliczmy liczbę wszystkich wyników sprzyjających zdarzeniu:

B - w każdym kontrolowanym pokoju pracuje więcej niż jedna osoba personelu

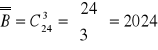
Ponieważ wszystkie wyniki są jednakowe prawdopodobne, więc prawdopodobieństwo:

 P(B) =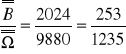

c)

Obliczmy liczbę wszystkich wyników sprzyjających zdarzeniu:

C' - przeciwnego do C - kontroli zostanie poddane co najmniej 5 osób

Ponieważ wszystkie wyniki są jednakowe prawdopodobne, więc prawdopodobieństwo:

  P(C') =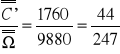

Korzystając z własności prawdopodobieństwa obliczamy:

P(C) = 1 - P(C') = 1 -

Zadanie 4

Ze zbioru Z =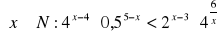 
losujemy ze zwracaniem kolejno dwie liczby. Obliczyć prawdopodobieństwo zdarzeń:

A - suma wylosowanych liczb jest większa od 8,

B - obie wylosowane liczby są równe.

 Rozwiązanie

1. Najpierw wyznaczamy zbiór Z, rozwiązując podaną nierówność.

2. Korzystamy z twierdzenia o iloczynie potęg o tej samej podstawie - ustalmy, że będzie nią liczba 2. Wtedy

czyli  2(x-4) + [-1(5-x)] < x-3 +

Stąd po przekształceniach, otrzymujemy nierówność równoważną:    

2x - 10 <

3.   Rozwiązujemy tą nierówność stosując metodę rozwiązywania nierówności wymiernej (*):

(a)   Przenosimy wyrażenia na jedną stronę:  2x - 10 -
< 0

(b) Sprowadzamy do wspólnego mianownika:  

(c)   Wykonujemy redukcję wyrazów podobnych:

(d)    Zapisujemy w równoważnej postaci iloczynowej:

(2x² -10x - 12)x <0

(e)  Szukamy miejsc zerowych wielomianu: 

Są nimi liczby x = 0, x = -1 oraz x =6.

(f)  Szkicujemy wykres wielomianu (jest to wielomian stopnia 3 o dodatnim współczynniku przy najwyższej potędze)

-1 0 6

(g)   Odczytujemy z wykresu te wartości x, dla których wartości funkcji są ujemne: 

mamy tutaj

(*)   Czasami można nierówność taką rozwiązywać prościej, np. mnożąc obie strony przez x².

4. W ten sposób wyznaczyliśmy zbiór Z (To nie jest przestrzeń zdarzeń elementarnych - wyznaczając zbiór nic nie mówimy o doświadczeniu losowym !!!): 

Z = {1,2,3,4,5}.

5.  Określamy przestrzeń Ω (wypisujemy wszystkie zdarzenia elementarne!):

Ω = {(1,1),(1,2),(1,3),(1,4),(1,5),

(2,1),(2,2),(2,3),(2,4),(2,5),

(3,1),(3,2),(3,3),(3,4),(3,5),

(4,1),(4,2),(4,3),(4,4),(4,5),

(5,1),(5,2),(5,3),(5,4),(5,5)}

- losujemy kolejno (uwzględniamy porządek) i ze zwracaniem (wyniki mogą się powtarzać)

6. Przestrzeń liczy więc 25 zdarzeń jednakowo prawdopodobnych (ilość wariacji z powtórzeniami).

7. W tym zadaniu można wypisać wszystkie zdarzenia sprzyjające zdarzeniu A oraz te, które sprzyjają zdarzeniu B.

Mamy jako wynik:

A = {(4,5),(5,4),(5,5)}  i    B = {(1,1),(2,2),(3,3),(4,4),(5,5)}.

8. Otrzymujemy prawdopodobieństwa jako ilorazy liczebności (prawdopodobieństwo klasyczne)  P(A) =
  i  P(B) =
.

Zadanie 5

W każdej z dwóch urn jest 5 kul czarnych, 10 kul czerwonych i 6 kul białych. Obliczyć prawdopodobieństwo tego, że losując po jednej kuli z każdej urny, wyciągniemy dwie kule tego samego koloru.

Rozwiązanie: 

1. W tym zadaniu inaczej określamy przestrzeń zdarzeń elementarnych. Mianowicie, opisujemy ją słownie:

Zdarzeniem elementarnym jest każdy zbiór dwuelementowy utworzony z kul, które pochodzą z obu urn (po jednej z każdej).

2. Liczba zdarzeń elementarnych to iloczyn liczb kombinacji: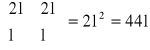
   

3. Zdarzeniu: „Wyciągniemy dwie kule tego samego koloru” sprzyjają zdarzenia: wylosowano dwie kule czarne (czyli 25 możliwości), dwie kule czerwone (100 możliwości) oraz dwie kule białe (36 możliwości).

4. Otrzymujemy więc łącznie: 161 zdarzeń elementarnych sprzyjających określonemu zdarzeniu.

Stąd szukane prawdopodobieństwo wynosi
.

5. Warto czasami spróbować sprawdzić wynik! 

Zobaczmy, ile jest zdarzeń sprzyjających zdarzeniu przeciwnemu do danego: "Wyciągniemy kule różnego koloru". Mamy teraz:   czarna - czerwona:  50, czarna - biała: 30, czerwona czarna: 50, czerwona biała: 60 oraz biała czarna: 30 i biała - czerwona:60. Razem 280 zdarzeń elementarnych. Gdy odejmiemy tą liczbę od 441 otrzymamy właśnie 161! A więc zgadza się.

---