Opracowanie ćwiczenia nr 5
Tabelka z wynikami pomiarów i obliczeniami:
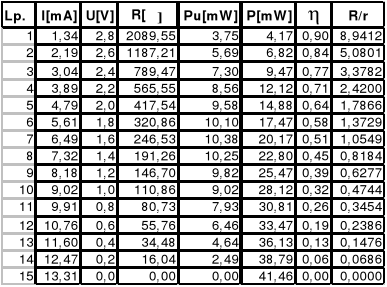
Opór obciążenia liczymy bezpośrednio z prawa Ohma wykorzystując wzór R=U/I.
Moc obliczamy z wzoru Pu=UI.
Wyniki obliczeń umieszczone są w tabelce.
Wykres zależności U=f(I).
Wykres zależności U(I) jest liniowy i ma równanie U=ε-I⋅r
Korzystając z metody graficznej odczytuje nieznane współczynniki, które wynoszą
ε=3,1126[V] natomiast r=0.2337[mΩ]=233,7[Ω] (r=0,2337[mΩ] bo prąd dany był w mA)
Do wyznaczenia błędu pomiaru Δε i Δr skorzystam z metody najmniejszych kwadratów.
![]()
W tym celu należy policzyć
(gdzie a=-0,2337 b=3,1126) następnie
![]()
![]()
Błąd Δε wynosi
![]()
natomiast Δr
Moc całkowitą obliczam z wzoru P=εI=ε2/(r+R)
natomiast sprawność η z zależności η=Pu/P
Wyniki umieszczone są w tabelce.
Z wykresu zależności Pu(R/r) wynika, że moc użyteczna osiąga wartość maksymalną dla oporu zewnętrznego równego oporowi wewnętrznemu źródła zasilania i wynosi Pu=ε2/4r,
natomiast moc całkowita P=ε2/2r. Dla powyższej wartości oporu odbiornika sprawność η=Pu/P=0,5.
Wnioski:
Siła elektromotoryczna badanego źródła zasilania wynosi ε=3,1126 ± 0,2248[V]
natomiast opór wewnętrzny r=233,7 ± 0,0018[Ω]
Z ćwiczenia wynika, że największą moc użyteczną można otrzymać dla odbiornika o oporze wewnętrznym równym oporowi wewnętrznemu źródła zasilania.
Ponadto można zauważyć, że największa sprawność jest osiągana dla małych natężeń prądy w obwodzie i spada ona wraz ze wzrostem prądu.
Duży spadek sprawności przy większym natężeniu wynika ze strat energii na oporze wewnętrznym źródła zasilania. Aby unikać takich strat należy budować źródła zasilania o małym oporze wewnętrznym jednak wiąże się z tym niebezpieczeństwo, że podczas zwarcia w obwodzie popłynie bardzo duży prąd.
![]()
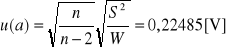
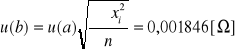
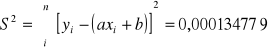
Wyszukiwarka
Podobne podstrony:
Opracowanie 10, agh wimir, fizyka, Fizyka(1)
konspekt Cw5, agh wimir, fizyka, Fizyka(1)
Opracowanie Cw6, agh wimir, fizyka, Fizyka(1)
Opracowanie Cw4, agh wimir, fizyka, Fizyka(1)
cw 1 - opracowanie, agh wimir, fizyka, Fizyka(1)
5 opracowanie, agh wimir, fizyka, Fizyka(1)
1 opracowanie, agh wimir, fizyka, Fizyka(1)
cw 2 - opracowanie, agh wimir, fizyka, Fizyka(1)
ćw 12 opracowanie, agh wimir, fizyka, Fizyka(1)
7 opracowanie, agh wimir, fizyka, Fizyka(1)
6 opracowanie, agh wimir, fizyka, Fizyka(1)
cw 13 - opracowanie, agh wimir, fizyka, Fizyka(1)
labolatorium2, agh wimir, fizyka, Fizyka(1)
10 moj konspekt, agh wimir, fizyka, Fizyka(1)
konspekt(1), agh wimir, fizyka, Fizyka(1)
samoindukcja cewki, agh wimir, fizyka, Fizyka(1)
Kospekt teoria, agh wimir, fizyka, Fizyka(1)
więcej podobnych podstron