Opracowanie wyników

	Sprężyna 1	Sprężyna 2
l0	15,5 cm	17 cm
M	35,4 g	88 g
d	0,94 mm	1,12 mm
D	11,4 mm	30 mm
n	158	126

l₀ - długość sprężyny bez obciążenia

M - masa sprężyny

d - średnica drutu

D - średnica zwoju

n - liczba zwojów

Ad.1 Metoda Statyczna

Sprężyna 1

g = 9,81 [m/s²]

obciazenie [kg]	wychylenie [m]	f=M*g [N]
0	0	0
0,0806	0,036	0,790686
0,0906	0,041	0,888786
0,108	0,045	1,05948
0,117	0,048	1,14777
0,1688	0,066	1,655928
0,232	0,092	2,27592
0,2838	0,11	2,784078
0,3486	0,133	3,419766
0,4006	0,151	3,929886
0,4636	0,175	4,547916
0,5154	0,193	5,056074

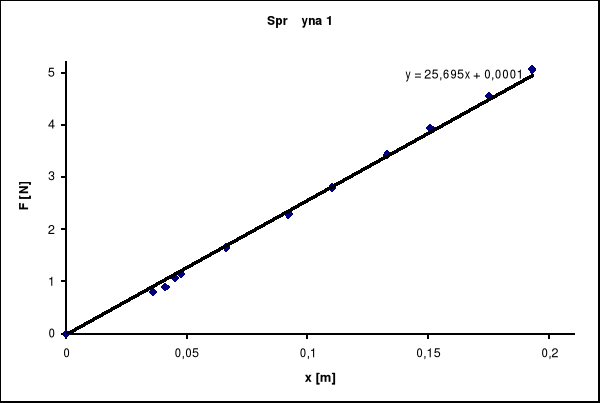
Wyznaczony metodą regresji liniowej współczynnik sprężystości jest równy współczynnikowi kierunkowemu prostej i wynosi k₁= 25,695 [kg/s²]

Niepewność wyznaczenia współczynnika k dla sprężyny 1 wynosi σ₁= 0,268539

Sprężyna 2

obciazenie [kg]	wychylenie [m]	f=M*g [N]
0	0	0
0,0806	0,156	0,790686
0,0906	0,175	0,888786
0,108	0,215	1,05948
0,117	0,234	1,14777
0,1616	0,328	1,585296
0,1688	0,341	1,655928

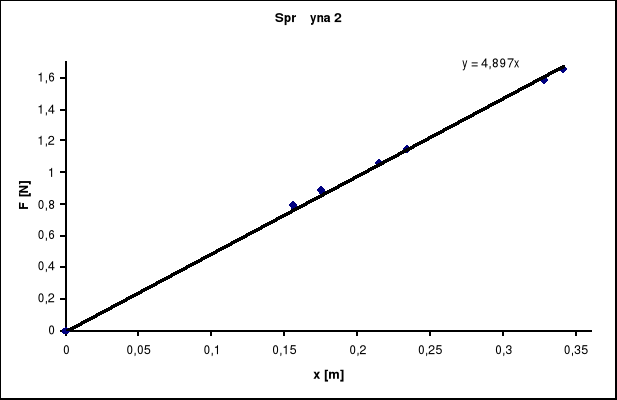
k₂ = 4,897 [kg/s²] σ₂= 0,06526

Ad.2 Metoda Dynamiczna

Sprężyna 1

obciazenie [kg]	czas 20 okresow [s]	sredni czas 1 okresu [s]	T^2 [s^2]
0,0806	7,35	0,3675	0,135056
0,1172	8,63	0,4315	0,186192
0,1692	10,13	0,5065	0,256542
0,2332	11,9	0,595	0,354025
0,2852	13,09	0,6545	0,42837
0,3488	14,44	0,722	0,521284
0,4008	15,35	0,7675	0,589056

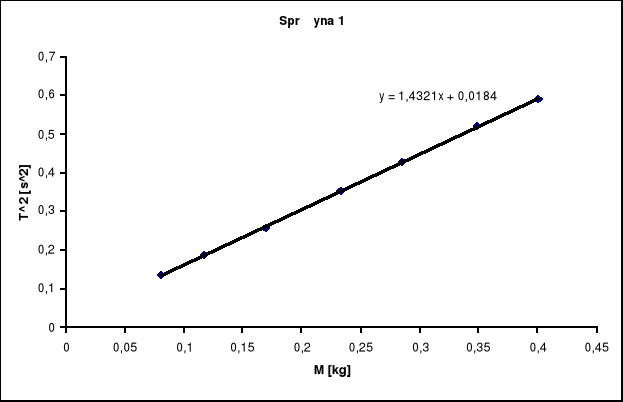
Współczynnik kierunkowy uzyskany z regresji liniowej wynosi a = 1,4321

Obliczam współczynnik sprężystości z zależności

Stąd k₁ = 27,5388 [kg/s²] , a niepewność σ₁= 0,01045

Sprężyna 2

obciazenie [kg]	czas 20 okresow [s]	sredni czas 1 okresu [s]	T^2 [s^2]
0,0806	19,19	0,9595	0,92064
0,0906	20,4	1,02	1,0404
0,108	21,25	1,0625	1,128906
0,1172	22,25	1,1125	1,237656
0,1616	25,4	1,27	1,6129
0,1692	25,56	1,278	1,633284

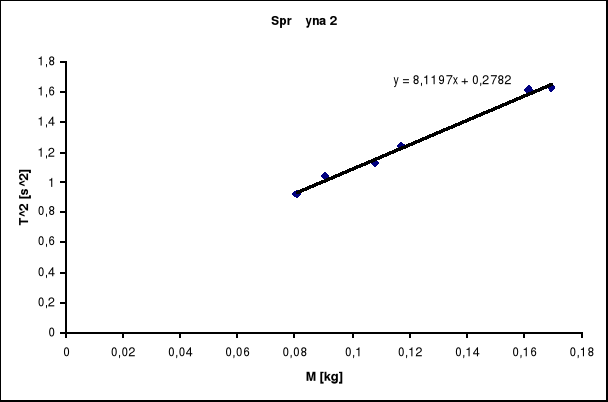
Współczynnik kierunkowy uzyskany z regresji liniowej wynosi a = 8,1197

Obliczam współczynnik sprężystości podobnie jak dla sprężyny 1:

Stąd k₂ = 4,8571 [kg/s²] , a niepewność σ₂= 0,30267

Porównanie metod

	Metoda statyczna	Metoda dynamiczna
Sprężyna 1	k1= 25,695 ± 0,26854 [kg/s^2]	k1 = 27,5388 ± 0,01045 [kg/s^2]
Sprężyna 2	k2 = 4,897 ± 0,06526 [kg/s^2]	k2 = 4,8571 ± 0,30267 [kg/s^2]

Jak widać z tabelki - pomiary współczynnika sprężystości obiema metodami są do siebie zbliżone, szczególnie dla sprężyny drugiej. Obie metody można uznać za skuteczne, lecz według mnie bardziej dokładna jest statyczna, ponieważ przy dynamicznej dochodzi nam czasem dość duży błąd związany z pomiarem czasu stoperem. Problemem jest także wprawienie sprężyny w idealnie pionowy ruch oscylacyjny.

Ad. 3 Moduł sztywności

	Sprężyna 1	Sprężyna 2
Promień drutu r [m]	0,00047	0,00056
Promień zwoju R [m]	0,0057	0,015
Liczba zwojów n	159	127

Moduł sztywności wyliczam z następującej zależności:

G₁ = 63561777911 [Pa] G₂ = 84029623887 [Pa]

Obliczam błąd wyznaczenia modułu sztywności z prawa przenoszenia błędów:

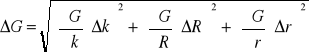
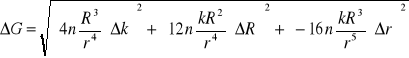
Sprężyna 1:

Błędy maksymalne:

Współczynnik sprężystości Δk = 0,3

Promień zwoju ΔR = 0,0002

Promień drutu Δr = 0,00002

ΔG₁ = 12501442815 [Pa]

Sprężyna 1:

Błędy maksymalne:

Współczynnik sprężystości Δk = 0,1

Promień zwoju ΔR = 0,002

Promień drutu Δr = 0,00002

ΔG₂ = 9274184032 [Pa]

---