Nr ćwicz. 202	Data: 20.03. 2012r.	Mateusz Kaczor	Wydział: BMiZ	Semestr II	Grupa ZP3 nr lab. 1
prowadzący dr Wanda Polewska			Przygotowanie:	Wykonanie:	Ocena ostat. :

Temat : Wyznaczanie siły elektromotorycznej ogniw metodą kompenensacji

I.Część teoretyczna

Źródłami siły elektromotorycznej nazywamy urządzenia zdolne do wytwarzania różnic potencjałów pomiędzy dwoma punktami . Do źródeł SEM zaliczamy ogniwa , baterie i prądnice . Wewnątrz źródła ładunki dodatnie przemieszczają się w kierunku od potencjału ujemnego do potencjału dodatniego.

Zatem źródło SEM musi być zdolne do wykonywania pracy na zwiększenie energii ładunków , które do niego dopływają . Jeśli przeniesienie ładunku dq związane jest z wykonaniem pracy dW , wówczas SEM źródła prądu zdefiniowane jest następująco :

Jednostką SEM jest wolt .

Rzeczywiste źródła SEM posiadają opór wewnętrzny r.

Jeżeli ze źródła czerpiemy prąd i to różnica potencjałów Uz na zaciskach jest mniejsza od SEM :

Uz = - ri .

Do pomiaru SEM nie można więc użyć woltomierza ponieważ pobiera on pewną ilość prądu . SEM mierzy się metodą kompensacyjną . Schemat układu kompensacyjnego przedstawiony jest poniżej :

Stosując do tego układu II prawo Kirchhoffa (oczko abcd ) otrzymujemy :

.

Gdy w wyniku zmian oporów R1 i R2 osiągniemy wartość I2 = 0 wówczas powyższe równanie przyjmie postać :

.

Wstępnie w układzie wykorzystuje się wzorcowe ogniwo Westona , którego SEM wynosi 0=1.0183V .

Ogniwo Westona :

W drugiej części ćwiczenia ogniwo wzorcowe zastępuje się badanym ( SEM jest równe x ). W analogiczny sposób otrzymujemy równanie :

.

SEM nieznanego ogniwa :

.

2. Wykonanie ćwiczenia

Szukam przybliżonej wartości R₁ i R₂, przy których następuje kompensacja SEM ogniwa wzorcowego. ­I₂=0

Lp.	Opór wstępny [ၗ]	R1 [ၗ]	R2 [ၗ]	R1+ R2 [ၗ]	I1 [A]
1	8000	1734	6266	8000	0,00063
2	10000	2175	7825	10000	0,0005
3	12000	2600	9400	12000	0,00042

Z poniższej zależności wyznaczam wartość prądu I₁

Średnia wartość prądu I₁ i odchylenia standardowego wynosi

I₁ = 0,00051Ⴑ0,0001 [A]

Średnia wartość rezystancji R₁ i odchylenia standardowego

R₁=2169,67Ⴑ433,025 [ၗ]

Następnie korzystając z zależności wyznaczam średnią wartość SEM ogniwa wzorcowego

ၥ₀ = R₁ I₁

ၥ₀ = 2169,67თ0,00051=1,1065317[V]

Odchylenie standardowe obliczam z zależności

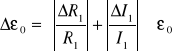
Zatem ostateczna wartość SEM ogniwa wzorcowego wynosi

ၥ₀ =1,1065317Ⴑ0,433 [V]

Szukam przybliżonej wartości R₁ i R₂, przy których następuje kompensacja SEM ogniwa badanego. ­I₂=0

Lp.	Opór wstępny [ၗ]	R1' [ၗ]	R2' [ၗ]	R1'+ R2' [ၗ]
1	8000	2053	5947	8000
2	10000	2566	7434	10000
3	12000	3079	8921	12000

Średnia wartość rezystancji R₁' oraz odchylenia standardowego przy badaniu ogniwa wzorcowego

R₁'= 2566Ⴑ 513 [ၗ]

Korzystając z poniższej zależności wyznaczam wartość SEM ogniwa wzorcowego

ၥ_x=R₁'I₁

Po podstawieniu do powyższego wzoru otrzymałem

ၥ_x =1,31864 [V]

Odchylenia standardowe wyznaczam z zależności

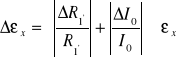
Ostateczny wynik wynosi

ၥ_x =1,31864Ⴑ0,0513 [V]

Wnioski

Otrzymana wartość siły elektromotorycznej SEM ogniwa wzorcowego jest bardzo zbliżona do wartości rzeczywistej ogniwa Westona. Ogniwo badane to najprawdopodobniej jakaś standardowa bateria.

---