Walidacja wyników

Wprowadzenie

Chemometria jest dziedziną chemii analitycznej, która przy wykorzystaniu metod statystycznych służy do wydobycia maksymalnej ilości informacji z danych pomiarowych. Jednym z jej działów jest walidacja, której celem jest sprawdzenie możliwości metody analitycznej pod względem takich kryteriów jak między innymi: precyzja i dokładność, granica wykrywalności i oznaczalności czy czułość i selektywność.

Selektywność metody analitycznej określa z

dolność metody lub instrumentu do odpowiedzi na obecność analitu przy braku odpowiedzi na inne składniki próby. Selektywność związana jest z rozdzielczością aparatu - większa rozdzielczość daje większą selektywność analizy.

Granica wykrywalności opisuje minimalne stężenie, które może być wykryte przy użyciu danej metody analitycznej. Najczęściej przyjmuje się, że równy jest on sumie średniej wartości tła plus trzykrotność odchylenia standardowego tła:

(1)

gdzie:

y_DL- granica wykrywalności;

y_B - średnia wartość tła;

s_B - odchylenie standardowe y_B

Granica oznaczalności jest kryterium ostrzejszym określającym takie stężenie substancji, które może być oznaczone ilościowo i jest zdefiniowane jako:

(2)

gdzie:

y_DL- granica wykrywalności;

a - współczynnik kierunkowy krzywej kalibracyjnej;

b - wyraz wolny krzywej kalibracyjnej_.

Czułość odpowiada nachyleniu krzywej kalibracyjnej. Jeśli zależność sygnału analitycznego y od stężenia analitu jest dana prostą y = ax + b, wówczas czułość jest zdefiniowana jako:

(3)

Dokładność określa różnicę pomiędzy uzyskaną wartością średnią a wartością prawdziwą

. Parametr ten związany jest z występowaniem błędów systematycznych.

Precyzja natomiast wynika z błędów przypadkowych i określa rozproszenie mierzonych wartości dookoła średniej i jest na ogół wyrażana poprzez odchylenia standardowe średniej.

Jednak podstawowym aparatem statystycznym używanym w laboratorium chemicznym jest szacowanie wartości rzeczywistej na podstawie danych pomiarowych oraz ocena zmienności tych danych. Najbardziej popularne wielkości będące oszacowaniem wartości oczekiwanej zostały przedstawione poniżej.

Moda - jest to wartość najczęściej występująca. Jeżeli w szeregu wyników nie powtarza się żaden, to zakres dzielimy na √n przedziałów o równej długości i sprawdzamy, w którym mieści się najwięcej wyników

Mediana - jest to wartość środkowa w zbiorze danych.

Wartość średnia ważona określona wzorem:

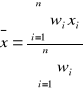
(4)

gdzie w_i oznacza wagę i-tego parametru wyrażoną wzorem:

(5)

C jest dowolną stałą o wymiarze kwadratu niepewności systematycznej. W praktyce przyjmujemy taką wartość, aby wagi były liczbami całkowitymi. Gdy w₁ = w₂ = ... = w_n wzór upraszcza się do postaci:

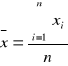
(6)

O wzajemnych relacjach pomiędzy tymi wartościami decyduje skośność, która wskazuje, czy rozkład jest symetryczny, prawo- (dodatnio) czy lewostronnie (ujemnie) asymetryczny. Dla przykładu, w przypadku skośności lewostronnej średnia przyjmuje wartość najmniejszą a moda największą, pomiędzy nimi znajduje się mediana (Rys.1).

Rys.1. Wzajemne relacje pomiędzy średnią, modą a medianą przy lewostronnej skośności rozkładu zmiennej.

Rys. 2. Charakter rozkładu zmiennej w zależności od wielkości skośności.

Innym parametrem określającym charakter rozkładu jest kurtoza, która wskazuje, czy rozkład wyników ma charakter płaski czy wydłużony w stosunku do rozkładu normalnego.

Oprócz oszacowania wartości rzeczywistej analityk musi także określić zmienność mierzonej wielkości. Najbardziej popularne parametry stosowane do oceny zmienności to rozstęp, wariancja i odchylenie standardowe.

Rozstęp - różnica między największą i najmniejszą wartością w serii danych

Wariancja i odchylenie standardowe - wariancja, będąca momentem drugiego rzędu odgrywa w statystyce ważną rolę, jednakże częściej używa się pierwiastka kwadratowego z jej wartości nazwanego odchyleniem standardowym:

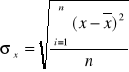
(7)

W czasie wykonywania analizy może zdarzyć się sytuacja, w której otrzymany wynik obarczony będzie tzw. błędem grubym, wynikającym z niepoprawnego przeprowadzenia pomiaru. Może on w znaczący sposób zmienić wartości średniej i odchylenia standardowego. W celu eliminacji takich wyników używa się testów statystycznych, pozwalających je wykrywać. Stosunkowo prosty i popularny test Q-Dixona polega na wyznaczeniu parametru Q i porównaniu uzyskanego wyniku z wartościami krytycznymi (Tabela 1):

(8)

gdzie:

x_nw - wynik najbliższy wątpliwemu;

x_w - wynik wątpliwy;

R - rozrzut

W praktyce laboratoryjnej zdarza się, że w celu lepszego oszacowania mierzonej wartości używa się różnych metod analitycznych do oceny jej wielkości. Do porównania dwóch średnich otrzymanych za pomocą odmiennych technik analitycznych albo wartości wzorcowej z wartością średnią służą testy u i u_o Lorda. Celem testów jest wykazanie istnienia bądź braku statystycznie znaczących różnic pomiędzy porównywanymi wartościami. W celu przeprowadzenia tych testów należy obliczyć należy ilorazy:

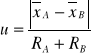
lub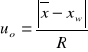
(9)

i porównać z wartościami krytycznymi przedstawionymi w tabeli 2, przy założonym poziomie istotności. Warunkiem przeprowadzenia testu u-Lorda jest równość liczby pomiarów w seriach A i B.

Tab.1. Wartości krytyczne Q_k w teście Q - Dixona.

ilość wyników	poziom ufności
		0,95	0,99
3	0,941	0,988
4	0,765	0,889
5	0,642	0,760
6	0,560	0,698
7	0,507	0,637
8	0,468	0,590
9	0,437	0,555
10	0,412	0,527

Tab.2. Wartości krytyczne w testach u- i u_o-Lorda.

		1 - α
		0,95		0,99
			uo	u	uo	u
n	2	6,353	1,714	31,828	3,958
		3	1,304	0,636	3,008	1,046
		4	0,717	0,406	1,3016	0,618
		5	0,507	0,306	0,843	0,448
		6	0,399	0,250	0,628	0,357
		7	0,333	0,213	0,507	0,300

Ćwiczenie:

Przeprowadzono analizę AAS dwóch próbek gleby na obecność ołowiu.

Uzyskane wyniki przedstawiono w Tabeli 3. Przeprowadzić analizę statystyczną danych, porównać uzyskane średnie.

Tab. 3. Przykładowe dane analityczne.

próba A	próba B
46,58	46,12
75,32	69,32
68,39	66,58
77,25	81,24
66,21	69,57
69,22	66,99
64,11	71,24

Pierwszym etapem analizy statystycznej jest znalezienie wyników obarczonych błędem grubym. W tym celu porządkujemy wartości rosnąco (malejąco) i wyliczamy rozstęp, czyli różnicę pomiędzy minimum i maksimum w naszych seriach. Następnie obliczamy wartości różnic pomiędzy wartościami: najniższą (najwyższą) a sąsiadującą. Wyniki obliczeń zostały zebrane w Tabeli 4.

Tab.4. Wyniki testu Q-Dixona.

test Q-Dixona	Próba A	Próba B
rozstęp	30,67	35,12
Qmin	0,572	0,583
Qmax	0,262	0,285

Porównując wartości Q z Tabeli 4 z wartościami krytycznymi widać, że w przypadku wartości najniższych Q_min>Q_k - pomiary te obarczone są błędem grubym i należy je pominąć w dalszych etapach analizy. Wyliczając poszczególne parametry statystyczne posłużono się programem Microsoft Excell, korzystając z zawartych w nim funkcji statystycznych. Wyniki analiz zebrano w Tabeli 5.

Tab. 5. Analiza statystyczna danych pomiarowych z Tabeli 3.

Parametr	próba A	próba B
średnia arytmet.	70,08	70,82
o. standard.	5,16	5,39
mediana	68,81	69,45
kwartyl dolny	66,76	67,57
kwartyl górny	69,22	71,24
IQR	7,40	11,00
skośność	0,51	1,90
kurtoza	-1,41	3,98
rozstęp	13,14	14,66
test  Lorda	0,027

Z powyższych wyliczeń można wyciągnąć następujące wnioski:

• odchylenie standardowe w obu próbach przyjmuje zbliżone wartości, świadczy to o podobnej precyzji obu serii pomiarowych,

• wartość mediany jest niższa od wartości średniej, związane jest to z prawoskośnym rozkładem wartości pomiarowych (skośność > 0)

• wyliczona wartość  testu -Lorda jest dużo niższa od wartości krytycznej dla poziomu istotności =0,95 i wskazuje na brak statystycznie istotnych różnic w dwóch seriach danych.

Literatura

1. J. Mazerski, Podstawy chemometrii, Wyd. Politechniki Gdańskiej, Gdańsk 2001,

2. K. Zając, Zarys metod statystycznych, PWE, Warszawa 1971,

3. R. Wódzki, Zastosowanie informatyki w chemii, Wyd. UMK, Toruń, 1999,

4. J.B. Czermiński, A. Iwasiewicz, Z. Paszek, A. Sikorski, Metody statystyczne dla chemików, PWN, Warszawa 1992

5. J. Chatłas, Ćwiczenia laboratoryjne z chemii nieorganicznej, Wydaw. UMK, Toruń 1995.

152

---