Praca zaliczeniowa z ekonometrii

Do budowy modelu wykorzystałem dane ze strony Głównego Urzędu Statystycznego http://www.stat.gov.pl. Dotyczą one produkcji sprzedanej (w 2001 r.) wg województw w zależności od przeciętnego wynagrodzenia brutto i liczby ludności (stan w dniu 30 IX 2001 r). Wszelkie obliczenia parametrów modelu ekonometrycznego są wykonane w arkuszu Microsoft Excel. Dane wyjściowe zawiera poniższa tabela:

	y	x1	x2
Dolnośląskie	30844,6	2234,45	2971,3
Kujawsko-pomorskie	20893,7	1911,30	2100,4
Lubelskie	11255,1	1889,18	2229,7
Lubuskie	9212,8	1792,71	1024,8
Łódzkie	25475,9	1869,68	2636,5
Małopolskie	28410,7	2075,94	3240,9
Mazowieckie	91396,5	2680,60	5077,9
Opolskie	10818,4	2038,58	1082,0
Podkarpackie	16968,0	1876,67	2130,7
Podlaskie	7630,4	1840,74	1220,4
Pomorskie	24532,0	2138,76	2203,9
Śląskie	73997,5	2461,73	4837,3
Świętokrzyskie	9514,0	2044,23	1321,0
Warmińsko-mazurskie	10852,9	1945,57	1469,0
Wielkopolskie	43865,0	1982,16	3365,4
Zachodniopomorskie	14180,0	2069,56	1735,0

gdzie:

Y - wielkość produkcji sprzedanej w mln zł

X1 - przeciętnego wynagrodzenia brutto w zł

X2 - liczba ludności ogółem w tysiącach

1. Oszacowanie parametrów modelu ekonometrycznego Metodą Najmniejszych Kwadratów (MNK)

Postać ogólna modelu:

Y = α₀ + α₁X1 + α₂X₂ + ζ_t

Postać modelu po oszacowaniu (MNK):

Y = - 72013 + 32,0787X₁ + 13,6679X₂

(19585,62) (11,45) (2,2)

2. Interpretacja parametrów strukturalnych

α₀ - wyraz wolny oszacowano na poziomie -72013 ze średnim błędem szacunku Ⴑ 19585,62.

α₁ - jeżeli przeciętne wynagrodzenie brutto zmieni się o 1 zł, to produkcja sprzedana zmieni się o 32,0787 liczba mln ze średnim błędem szacunku Ⴑ 11,45 mln.

α₂ - jeżeli liczba ludności zmieni się o 1 tysiąc, to produkcja sprzedana zmieni się o 13,6679 mln ze średnim błędem szacunku Ⴑ 2,2 mln.

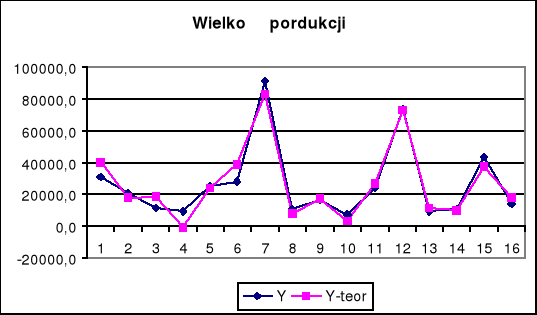
3. Interpretacja ogólnych miar dopasowania

Współczynnik R² = 0,941; 94,1 % zmienności zmiennej objaśnianej - wielkość produkcji sprzedanej zastało wyjaśnione przez model.

Współczynnik φ² = 0,059; 5,9 % zmienności zmiennej objaśnianej - wielkość produkcji sprzedanej nie zastało wyjaśnione przez model.

Błąd standardowy reszt S_e = 6300,94; Przeciętne odchylenie pomiędzy rzeczywistą ilością produkcji sprzedanej a ilością sprzedaną na podstawie modelu wynosi 6300,94 mln.

Współczynnik zmienności losowej V_s = 23,454 % ; Przeciętne odchylenie wartości teoretycznych od empirycznych zmiennej objaśnianej stanowi 23,454% przeciętnego poziomu tej zmiennej (wielkość produkcji sprzedanej).

4. Badanie istotności parametrów strukturalnych

H_o:α₁ = 0

H₁:α₁ Ⴙ 0

t _α0 = 0,000188 < 2

Brak podstaw do odrzucenia hipotezy zerowej H_o na korzyść hipotezy alternatywnej H₁

t _α1 = 2,45E-01 < 2

Brak podstaw do odrzucenia hipotezy zerowej H_o na korzyść hipotezy alternatywnej H₁

t _α2 = 2,82 > 2

Odrzucamy hipotezę alternatywną H₁ na korzyść hipotezy zerowej H_o

5. Test F - Fishera

H_o: wszystkie α = 0

H₁: chociaż jedno α Ⴙ 0

F = 103,508

F _0,05;13;2 = 3,81

Brak podstaw do odrzucenia hipotezy H_o na korzyść hipotezy alternatywnej H₁

6. Badanie symetrii składnika losowego

m - liczba reszt dodatnich

n - liczba reszt

H_o:[m/n = 0,5]

H₁:[m/n Ⴙ 0,5]

m = 7, n = 16

t = 0,503

t_0,05,15 = 2,131

Nie ma podstaw do odrzucenia hipotezy zerowej H_o o symetrii składnika losowego.

---