Rozwiąż nierówność
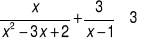
Wykaż, że kwadrat liczby niepodzielnej przez 3 przy dzieleniu przez 3 daje resztę 1.
Wykaż, że dla dowolnych liczb rzeczywistych a, b i c prawdziwa jest nierówność
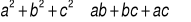
Znaleźć wszystkie funkcje

, dla których zachodzi równość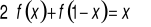
. Zadanie można rozwiązać w następujący sposób:
podstawiamy do danego równania w miejsce x wyrażenie 1-x:
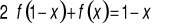
rozwiązując układ równań
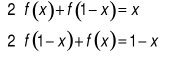
(traktując f(x) i f(x-1) jako niewiadome) otrzymujemy wzór funkcji f: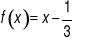
W podobny sposób
Znajdź wszystkie funkcje

, dla których zachodzi równość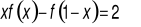
Znajdź wszystkie funkcje
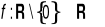
, dla których zachodzi równość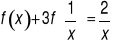
Dla jakich wartości parametru m równanie
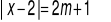
ma
a) jedno rozwiązanie b) dwa rozwiązania
Określ liczbę pierwiastków równania

w zależności od wartości parametru k.Wyznacz wszystkie wartości x, dla których nierówność

jest prawdziwa dla każdego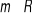
.Wielomian
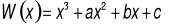
jest podzielny przez trójmian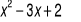
i przy dzieleniu przez dwumian x+1 daje resztę -24. Wyznacz współczynniki a, b i c.Rozwiąż równanie:
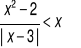
Jednym z miejsc zerowych funkcji
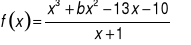
jest 5.Znajdź współczynnik b.
Znajdź pozostałe miejsca zerowe funkcji f.
Wyznacz przedziały monotoniczności funkcji f.
Rozwiąż równanie
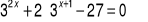
Rozwiąż układ równań
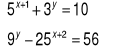
Funkcja g określona jest wzorem
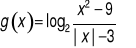
Wyznacz dziedzinę funkcji g.
Narysuj wykres funkcji g.
Sporządź wykres funkcji, która każdej liczbie rzeczywistej m przyporządkowuje liczbę rozwiązań równania g(x)=m
Sprawdź, czy podana równość jest tożsamością trygonometryczną:
a) ![]()
b) ![]()
Wyznacz zbiór wartości funkcji

. Rozwiąż równanie f(x)=4Dla jakich wartości x liczby
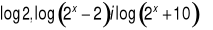
są kolejnymi wyrazami ciągu arytmetycznego? Oblicz różnicę tego ciągu.Rozwiąż układ równań
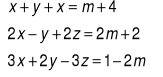
. Dla jakich wartości parametru m liczby x, y, z są kolejnymi wyrazami ciągu arytmetycznego?
Wyszukiwarka
Podobne podstrony:
MATURA ROZSZERZONA MATEMATYKA ARKUSZ
MATURA ROZSZERZONA MATEMATYKA ODPOWIEDZI
kadratowa rozszerzenie, Matematyka, Liceum
MATURA ROZSZERZONA MATEMATYKA ARKUSZ
matura rozszerzona matematyka 2017 cke
Matura 2010 matematyka poziom rozszezony Testy Operon
Matematyka nr 1, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
MATEMATYKA (rozszerzony) probna 2008, PROBNA MATURA GRU2007 Matematyka PR odp
Zadania dla maturzystów na dzień 28 marca 2010, matematyka, LICEUM, arkusze maturalne, Nowy folder (
Matura 16 matematyka poziom rozszerzony odpowiedzi
matura3, Matematyka, Liceum
Matematyka nr 2, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
Matematyka nr 7, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
Matematyka nr 8, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
Fizyka nr 4, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
Matura 2016 matematyka poziom rozszerzony
Fizyka nr 2, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
Fizyka nr 1, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
więcej podobnych podstron