Zajęcia nr 7 - matematyka, 12 czerwca 2010

Równanie prostej: y=ax+b lub Ax+By+C=0 (czyli
)

Równanie prostej przechodzącej przez dwa punkty - rozwiązać układ równań:

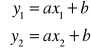
Współczynnik kierunkowy prostej równoległej do prostej y=ax+b jest równy a.

Współczynnik kierunkowy prostej prostopadłej do prostej y=ax+b jest równy
.

Odległość A(x_A,y_A) i B(x_B,y_B) w układzie współrzędnych:

Środek odcinka A(x_A,y_A) i B(x_B,y_B) :

Równania okręgu:

lub
, gdzie (a,b) - współrzędne środka okręgu, r - jego promień, c=a²+b²- r² .

Odległość punktu A(x₀,y₀) od prostej Ax+By+C=0: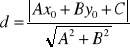

Dany jest punkt A(x,y).

Punkt symetryczny do A względem osi OX ma współrzędne A'(x,-y).

Punkt symetryczny do A względem osi OY ma współrzędne A'(-x, y).

Punkt symetryczny do A względem środka układu współrzędnych ma współrzędne A'(-x,-y).

Zad.1.

Oblicz odległość punktu A od środka odcinka BC, gdzie A=(1,3), B=(4, 7), C=(-2, -3).

Zad.2.

Punkt B =(-1,9) należy do okręgu stycznego do osi OX w punkcie A=(2,0) . Wyznacz równanie tego okręgu.

Zad.3.

Ile punktów wspólnych ma okrąg o równaniu
z prostą o równaniu
?

Zad.4.

W układzie współrzędnych na płaszczyźnie zaznaczono punkty A=(2,0) i B=(4,0). Wyznacz wszystkie możliwe położenia punktu C, dla których ABC jest trójkątem równoramiennym o podstawie AB i polu równym 3.

Zad.5.

Dane są proste o równaniach l: 4x+2y-5=0 i k:mx+3y+1=0. Wyznacz parametr m, tak aby te proste były prostopadłe.

Zad.6.

Dane są punkty A=(-2,-7), B=(-1,-4), C=(4,11). Wykaż, że te punkty są współliniowe.

Zad.7.

Dany jest koniec odcinka A=(-4,-7) i jego środek S=(5,-1). Wyznacz współrzędne drugiego końca tego odcinka.

Zad.8.

Odcinek AB jest wysokością trójkąta równobocznego. Oblicz długość boku trójkąta, jeśli wiadomo, że A=(-3,-2), B=(5,2).

Zad.9.

Oblicz pole, obwód i długość wysokości poprowadzonej z punktu C trójkąta ABC, gdzie A=(-2,-7), B=(-1,-4),C=(4,0).

Zad.10.

Dana jest prosta l o równaniu y=3x-1 i punkt A=(6,2). Wyznacz punkt B symetryczny do punktu A względem prostej l.