Zajęcia nr 3 - matematyka, 20 marca 2010

Wyjaśnienie wpadki z poprzednich zajęć

Gdyby pewna partia polityczna miała 200 popierających ją osób i poparcie wzrosło o 2 % to popierałoby ją wówczas 1,02თ200=204 osoby (nie ważna jest ilość wszystkich wyborców - obliczamy 2% z konkretnej liczby).

Gdyby partia polityczna miała 200 popierających ją osób i np. było to 10% elektoratu, czyli wszystkich wyborców byłoby 2000 (10% z x =200). Jeśli teraz poparcie wzrosło o dwa punkty procentowe, to poparcie dla partii wyniosłoby 12%, czyli 0,12თ2000=240 - tylu wyborców z całego stałego elektoratu popierałoby partię ( przy punktach procentowych ważna jest liczba wszystkich wyborców).

Zadanie o sprzedaży raz jeszcze

U producenta

Producent sprzedawał po 88 zł brutto.

Cena netto u producenta bez 7% VAT: 1,07x=88, stąd x*82,24 zł.

Producent obniża cenę netto o 5%: 0,95თ82,24*78,13 zł.

Producent sprzedaje teraz z 22 % VAT: 1,22თ78,13*95,32 zł - nowa cena brutto u producenta.

U sprzedawcy

Marża przed zmianami u sprzedawcy: 15 % z 88 zł = 13,2 zł.

Cena u sprzedawcy przed zmianami: 88zł + 13,2 zł =101,2 zł

Marża u sprzedawcy maleje o 3 punkty procentowe!, czyli wynosi 12 %.

(Uwaga - jeszcze jedno dodatkowe wyjaśnienie procent i punktów procentowych: gdyby marża zmalała o 3% to wyniosłaby 97%z 13,2 zł = 12,8 zł)

Marża po zmianach u sprzedawcy: 12 % z 95,32 zł *11,44 zł.

Obecna cena towaru u sprzedawcy (czyli po wszystkich zmianach): 1,12თ95,32 zł * 106,76 zł.

Odpowiedzi:

Cena wzrosła o 106,76 zł - 101,2 zł = 5,56 zł w stosunku do pierwszej ceny, czyli 101,2 zł.

Marża zmalała zatem o 13,2 zł - 11,44 zł = 1,76 zł w stosunku do marży wynoszącej 13,2 zł.

Zatem

Przykład wart ponownej analizy.

Równania i nierówności kwadratowe

Równanie kwadratowe - równanie postaci

Dla równania kwadratowego wyznaczamy

Jeśli
, równanie nie posiada rozwiązań.

Jeśli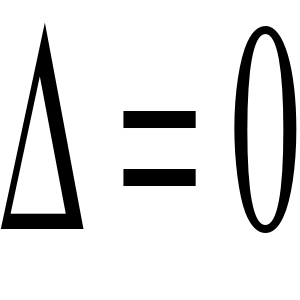
, równanie ma jedno rozwiązanie

Jeśli
, równanie ma dwa rozwiązania
oraz

Równanie można zapisać w postaci iloczynu:

Rozwiązaniem nierówności kwadratowej:

jest suma przedziałów

jest przedział

jest przedział

jest suma przedziałów

Przy nierównościach typu
lub
należy w rozwiązaniach domknąć przedziały przy
, np.:

Wzory:

Liczba odcinków i boków n-kąta wypukłego:

Liczba przekątnych n-kąta wypukłego:

Ćwiczenia do zajęć nr 3:

1. Rozwiąż równania:
   ,
   .
   ,

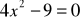
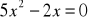
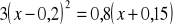
2. Rozwiąż równanie:
   

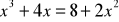
3. Rozwiąż nierówności:
   ,
   ,
   ,

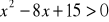
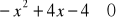
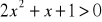
4. Rozwiąż równanie
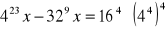
   , a wynik przedstaw w postaci 2^k, gdzie k jest liczbą całkowitą.

5. Rozwiąż równanie:
   

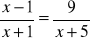
6. Oblicz długości boków prostokąta którego obwód wynosi 39 cm, a pole 90 cm².

7. Suma kwadratów trzech kolejnych liczb naturalnych wynosi 434. Znajdź te liczby.

8. Liczbę 15 rozłóż na dwa składniki, których suma kwadratów wynosi 117.

9. Ile wierzchołków ma wielokąt wypukły , który ma 90 przekątnych?

10. W jakim wielokącie łączna ilość boków i przekątnych wynosi 36?

11. Obwód trójkąta prostokątnego jest równy 30, a suma długości przyprostokątnych jest o 4 większa od długości przeciwprostokątnej. Oblicz długości boków tego trójkąta.

12. W czasie wycieczki rowerowej uczniowie mieli do przebycia trasę długości 84 km. Podzielili tę trasę na odcinki równej długości i codziennie przejeżdżali wyznaczony odcinek. Gdyby na przebycie całej trasy zużyli o dwa dni więcej, to mogliby dziennie przebywać o 7 km mniej. Ile kilometrów przebywali uczniowie dziennie?

13. Dwaj pasterze prowadzą swoje stadka owiec. Pierwszy mówi do drugiego: „Daj mi jedną owcę, a będę miał dwa razy więcej owiec niż ty”. Z kolei drugi mówi do pierwszego: „Daj mi ty jedną owcę, a będziemy mieć równo”. Ile owiec miał każdy z nich?

14. Dwa okręgi są styczne zewnętrznie, a odległość ich środków jest równa 19. Gdyby te okręgi były styczne wewnętrznie, to ta odległość wynosiłaby 5. Wyznacz długości promieni tych okręgów.

Uwaga - zaległa godzina z 6 marca zostanie przeznaczona na logarytmy.

---