Nie wyznaczając pierwiastków równania
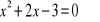
oblicz wartość wyrażeń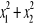
,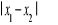
,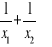
,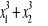
.Wyznacz, dla jakich wartości parametru m równanie ma dwa różne pierwiastki tego samego znaku:
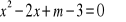
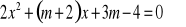
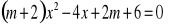
Wyznacz, dla jakich wartości parametru m równanie ma dwa pierwiastki o różnych znakach:
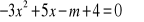
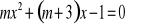
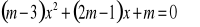
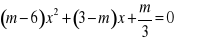
Wyznacz, dla jakich wartości parametru m równanie ma dwa różne pierwiastki dodatnie:
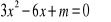
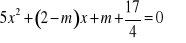
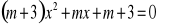
Wyznacz, dla jakich wartości parametru m równanie ma dwa różne pierwiastki ujemne:
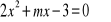
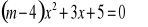
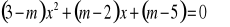
Dla jakich wartości parametru m iloczyn różnych pierwiastków równania
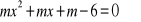
jest większy od -3?Dla jakich wartości parametru m suma różnych pierwiastków równania
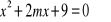
jest równa ich iloczynowi?Dane jest równanie
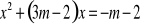
z niewiadomą x. Sformułuj warunki, jakie powinien spełniać parametr m, by równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.Wyznacz wszystkie wartości parametru m, dla których równanie
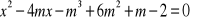
ma dwa różne pierwiastki rzeczywiste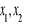
takie, że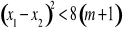
Funkcja kwadratowa
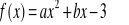
, gdzie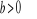
posiada dwa różne miejsca zerowe, których iloczyn jest równy -3. Wiedząc, że funkcja przyjmuje najmniejszą wartość -4, wyznacz:współczynniki a i b,
miejsca zerowe funkcji f.
Dla jakich wartości parametru m, równanie
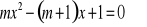
ma dokładnie jedno rozwiązanie?Wyznacz wszystkie liczby całkowite k, dla których funkcja
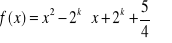
przyjmuje wartości dodatnie dla każdego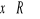
.Wyznacz wszystkie wartości parametru m, dla których równanie
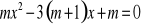
nie ma rozwiązania w zbiorze liczb rzeczywistych.Rozwiąż równania:
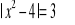
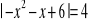
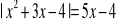
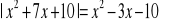
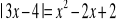
Narysuj wykres funkcji
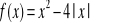
i na jego podstawie wyznacz liczbę rozwiązań równania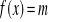
w zależności od parametru m.Rozwiąż nierówności:
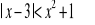
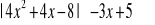
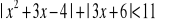
Wyszukiwarka
Podobne podstrony:
matura rozszerzenie, Matematyka, Liceum
okrag wpisany i opisany, Matematyka, Liceum
Wok Romańska, matematyka liceum
Matematyka nr 1, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
kwadratowa, Matematyka, Liceum
wykladnicza, Matematyka, Liceum
homograficzna, Matematyka, Liceum
wartość bezwzględna2, Matematyka, Liceum
PLAN WYNIKOWY FIZYKA ZSZ, fizyka, poz rozszerzony, Fizyka Liceum
Zadania dla maturzystów na dzień 28 marca 2010, matematyka, LICEUM, arkusze maturalne, Nowy folder (
stereometria, matematyka, liceum
matura3, Matematyka, Liceum
matematyka', liceum
notacja wykładnicza, Matematyka, Liceum
zadania2, Matematyka, Liceum
ciąg geometryczny, Matematyka, Liceum
Matematyka nr 2, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
więcej podobnych podstron