CIĄGI LICZBOWE

Zad.1

Pierwszy wyraz ciągu arytmetycznego jest równy 30, różnica zaś wynosi -3. Ostatni wyraz ciągu stanowi 0,125 sumy wszystkich poprzednich wyrazów. Wyznaczyć ilość wyrazów ciągu i ich sumę.

Zad.2

Trzy liczby dodatnie tworzą ciąg geometryczny. Suma tych liczb jest równa 26, natomiast suma

ich odwrotności wynosi. Znajdź te liczby.

Zad.3

Ile wyrazów ciągu arytmetycznego, w którym , r = 4 należy dodać, aby ich suma

była równa granicy ciągu określonego wzorem: .

Zad.4

Obliczyć trzeci wyraz ciągu , jeżeli jest on ciągiem geometrycznym oraz

i .

Zad.5

Wyznaczyć ciąg arytmetyczny, którego pierwszy wyraz jest równy 2 oraz wyrazy pierwszy, trzeci

i jedenasty tego ciągu tworzą ciąg geometryczny.

Zad.6

Długości dwóch kolejnych boków prostokąta i jego przekątnej tworzą ciąg arytmetyczny. Obliczyć długości boków tego prostokąta wiedząc, że jego pole jest równe 108.

Zad.7

Zbadać monotoniczność i obliczyć granice ciągów o wyrazach ogólnych:

, .

Zad.8

Długości krawędzi prostopadłościanu tworzą ciąg geometryczny. Objętość prostopadłościanu wynosi 8, zaś długość przekątnej . Obliczyć długości krawędzi prostopadłościanu.

Zad.9

Obliczyć wartość wyrażenia: , gdzie 0,(1) oznacza ułamek okresowy.

Zad.10

Dany jest nieskończony ciąg geometryczny postaci:
.

Wyznacz wszystkie wartości p, dla których granicą ciągu jest liczba:

1. 0.

2. 2

Zad.11

Dla jakich wartości parametru k ciąg ma granicę równą 2?

Zad.12

Trzy pierwiastki wielomianu o współczynnikach całkowitych są kolejnymi wyrazami ciągu arytmetycznego. Suma ich wynosi 21, a ich iloczyn 315. Wykazać, że dla każdej liczby nieparzystej wielomian ten przyjmuje wartość podzielną przez 48.

Zad.13

Rozwiązać nierówność dla x>0

Zad.14

Dana jest funkcja określona wzorem:

gdzie prawa strona jest sumą nieskończonego ciągu geometrycznego. Wyznaczyć dziedzinę,

zbadać okresowość i parzystość tej funkcji.

Zad.15

Rozwiąż równanie:

Zad.16

Wyznaczyć ciąg arytmetyczny wiedząc, że suma n-wyrazów jest określona wzorem:

Zad.17

W nieskończonym ciągu geometrycznym suma wyrazów o numerach nieparzystych jest równa 24, a suma wyrazów o numerach parzystych jest równa 12. Wyznacz ten ciąg.

Zad.18

Trzy liczby, których suma wynosi 124 są kolejnymi wyrazami ciągu geometrycznego. Jeżeli do pierwszej z tych liczb dodamy 1, drugą zostawimy bez zmian, a od trzeciej odejmiemy 65, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Znajdź te liczby.

Zad.19

Rozwiąż nierówność: .

Zad.20

Dany jest ciąg

1. Udowodnić, że jest on ciągiem geometrycznym.

2. Dla jakich p ciąg ten jest malejący?

Zad.21

Korzystając z zasady indukcji matematycznej, udowodnij, że każda liczba naturalna
spełnia nierówność:

Zad.22

Ciąg liczbowy
jest określony dla każdej liczby naturalnej
wzorem
, gdzie
.

1. Wykaż, że dla każdej wartości p ciąg
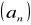
   jest arytmetyczny.

2. Dla p = 2 oblicz sumę
   .

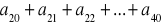
3. Wyznacz wszystkie wartości p, dla których ciąg
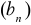
   określony wzorem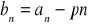
   jest stały.

Zad.24

Dany jest ciąg
, gdzie
dla każdej liczby naturalnej.

1. Zbadaj monotoniczność tego ciągu;

2. Oblicz
   

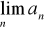
3. Podaj największą liczbę a i najmniejszą liczbę b takie, że dla każdego n spełniny jest warunek
   .

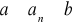
Zad.25

Wykaż, że jeżeli liczby
są kolejnymi wyrazami ciągu geometrycznego, to liczby
są kolejnymi wyrazami ciągu arytmetycznego.

Zad.26

Dany jest ciąg o wyrazie ogólnym
.

1. Udowodnij, że wszystkie wyrazy tego ciągu są liczbami naturalnymi.

2. Który wyraz ciągu jest równy 5?

c) Różnica sześcianów dwóch kolejnych wyrazów tego ciągu jest równa (-1261). Wyznacz te wyrazy.

---