Sprawozdanie z ćwiczenia nr 6.

Temat ćwiczenia: LEPKOŚĆ

1. WSTĘP

Przedmiotem ćwiczenia jest badanie wpływu temperatury na lepkość cieczy.

Do pomiaru lepkości dynamicznej cieczy metodą opadającej kulki służy lepkościomierz Hopplera. Przyrząd składa się z metalowego korpusu i szklanego cylindra połączonego z termostatem, wewnątrz którego znajduje się kalibrowana szklana rurka pomiarowa.

2. OBLICZENIA

Lepkość dynamiczną oblicza się według uproszczonego równania Stokesa:

gdzie:

t - średni czas opadania kulki [s]

d_k, d_c - odpowiednio gęstości kulki i badanej cieczy [g/dm³]

K - stała ujmująca wszystkie niezmienne wartości występujące w równaniu

Stokesa, przyspieszenie ziemskie, promień kulki i drogę opadania

Zmierzyć czas opadania kulki w temperaturach: 20, 30, 40, 50 ,60⁰C

Wyniki pomiarów:

Temperatura cieczy [^0C]	Średnia arytmetyczna czasu opadania kulki [s]	Gęstość cieczy [g/cm^3]	Lepkość [cP]
20	109	1,2613	96,84
30	57	1,2552	50,68
40	31	1,2490	27,59
50	19	1,2423	16,93
60	12	1,2359	10,70

Stała K = 0,12908 [mPa cm³/g] d_k = 8,144 [g/cm³]

Zależność pomiędzy temperaturą a lepkością cieczy przedstawia równanie:

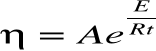
gdzie:

A - stała charakterystyczna dla danej cieczy

E - energia aktywacji lepkości

R - stała gazowa

T - temperatura bezwzględna

e - podstawa logarytmu naturalnego

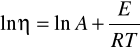
Logarytmując to równanie otrzymamy zależność:

t [^0c]	T [K]	1/T	Ln n
20	293	0,0034	4,57
30	303	0,0033	3,93
40	313	0,0032	3,32
50	323	0,0031	2,83
60	333	0,0030	2,37

Na podstawie wykresu zależności wyznaczyć wartości

stałych A i E.

Wyznaczanie parametrów równania liniowego postaci y = a+bx metodą graficzną:

Na osi X obieramy dwa dowolne punkty x₁ i x₂. Odczytujemy z wykresu wartości rzędnych tych punktów y₁ i y₂. Współczynnik kierunkowy prostej wyznacza się z zależności:

Wyraz wolny równania liniowego można wyznaczyć następująco:

a = y₁ - bx₁ lub a = y₂ - bx₂

a = y₁ - bx₁ = 2,37 - 5500 ∙ 0,0030 = -13,13

y = a+bx = bx+a

y = 5500x - 13,13

a = ln A b=E/R

A = e^a E=b∙R

A = e^-13,13 = 1,98∙10^-6 E = 5500∙8,315 = 45732,5

ZAKŁAD CHEMII FIZYCZNEJ

Temat ćwiczenia:

Lepkość.

Ćwiczenie wykonali:

Anna Keller;

Tomasz Kurasiński.

Wstęp teoretyczny:

Przedmiotem ćwiczenia jest badanie wpływu temperatury na lepkość cieczy. Do pomiaru lepkości dynamicznej cieczy metodą opadającej kulki służy lepkościomierz Hopplera. Przyrząd składa się z metalowego korpusu i szklanego cylindra połączonego z termostatem, wewnątrz którego znajduje się kalibrowana szklana rurka pomiarowa.

Lepkość dynamiczną oblicz się według uproszczonego równania Stockesa:

gdzie:

t - średni czas opadania kuli [s];

d_k - gęstość kuli [g/cm³];

d_c - gęstość badanej cieczy [g/cm³];

K - stała ujmująca wszystkie niezmienne wartości występujące w równaniu Stockesa (przyspieszenie ziemskie, promień kuli i drogę opadania).

Dane liczbowe:

d_k = 8,144 [g/cm³];

K = 0,12908 [mPa⋅cm³/g].

Zależność pomiędzy temperaturą a lepkością cieczy podaje nam równanie:

gdzie:

A - stała charakterystyczna dla danej cieczy;

E - energia aktywacji lepkości;

R - uniwersalna stała gazowa; - [8,314 J/(kmol⋅K)]

T - temperatura bezwzględna;

e - podstawa logarytmu naturalnego.

ZESTAWIENE DANYCH DOŚWIADCZALNYCH

Temperatura cieczy [°C]	Średni czas opadania [s]	Gęstość cieczy [g/cm^3]	Lepkość dynamiczna [cP]
20	260,0	1,2347	231,88
30	118,2	1,1664	106,46
40	64,4	1,1202	58,39
50	38,2	1,1136	34,67
60	24,0	1,1082	21,80

Graficzne wyznaczenie energii aktywacji lepkości i stałej „A” występujących w równaniu:

na podstawie wykresu lnη = f (1/T).

Po zlogarytmowaniu otrzymuje się:

Wzór regresji liniowej zależności lnη = f (1/T)

Y = 5727,5⋅X - 14,1744

Stąd:

-14,1744 = lnA A = e ^-14,1744 A = 6,985⋅10^-7

5727,5 = E/R E = 5727,5 ⋅ 8,314 E = 47618,4

Porównanie wartości lepkości obliczonej wg Stokesa i równania Arrheniusa - Guzmana .

Temperatura [K]	Lepkość wg Stokesa [cP]	Lepkość wg Guzmana [cP]
293	231,88	215,60
303	106,46	113,10
313	58,39	61,83
323	34,67	35,09
333	21,80	20,60

WNIOSKI:

Nie ma dotychczas uniwersalnego równania, które by pozwoliło obliczyć współczynnik lepkości dla dowolnej cieczy w dowolnej temperaturze. Dysponujemy natomiast metodami umożliwiającymi interpolację, a nawet ekstrapolację zależności lepkości od temperatury, jeżeli znamy dwie wartości współczynnika lepkości rozpatrywanej cieczy. Opracowano również sposoby przybliżonego wyznaczenia lepkości dla dowolnej temperatury przy znajomości tylko jednego punktu.

Na ogół zależność η = f (T) dają krzywe nie nadające się wprost do interpolacji, a to na skutek znacznej krzywizny.

Ogólna zależność lepkości od temperatury:

- im wyższa temperatura tym niższy współczynnik lepkości.

Opracowali:

Olszewski Bartłomiej

Michalski Maciej

Rok II grupa II

---