Wykonał: Jacek Cebulski Szczecin 06.11.01r.

Bartłomiej Biba

POLITECHNIKA SZCZECIŃSKA

ZAKŁAD CHEMII FIZYCZNEJ

Laboratorium studenckie

Sprawozdanie z wykonania ćwiczenia nr 9:

„Wyznaczanie ciepła parowania heksanu z pomiaru zależności prężności pary od temperatury.”

Teoria:

Efekty cieplne towarzyszą nie tylko reakcjom chemicznym, również takie procesy jak zmiana stanu skupienia (parowanie, kondensacja, topnienie, krystalizacja) czy proces rozpuszczania substancji chemicznych, związane są ze znacznymi efektami cieplnymi.

W procesie parowania cząsteczki cieczy znajdują się w równowadze termodynamicznej z cząsteczkami pary nasyconej o ciśnieniu p i temperaturze T.

Jeżeli przez G^(c) oznaczymy entalpię swobodną molową substancji w fazie ciekłej, zaś przez G^(g) w fazie gazowej, to zgodnie z druga zasada termodynamiki różniczki zupełne rozważanych entalpii swobodnych wynoszą:

dG_(c) = -S_(c)dT + V_(c)dp

dG_(g) = -S_(g)dT + V_(g)dp

gdzie S_(c) i S_(g) oznaczają entropię molową cieczy i pary, zaś V_(c) i V_(g) ich objętości molowe.

W stanie równowagi G_(c) =G_(g) i wobec tego

-S_(c)dT+V_(c)dp= -S_(g)dT+V_(g)dp

Po przekształceniu otrzymujemy równanie Clasiusa

gdzie ΔS=S_(g) - S_(c) oznacza entropię parowania, zaś ΔV=V_(g) - V_(c) zmianę objętości w procesie parowania.

Ponieważ parowanie jest procesem równowagowym, a stąd także odwracalnym, możemy entropię procesu wyrazić za pomocą ciepła parowania L_p w temperaturze T:

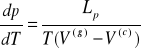
Dla równowagi ciecz-para, można przyjąć że, ciepło parowania nie zależy od temperatury, co jest w przybliżeniu słuszne dla małego przedziału temperatur. W dużym oddaleniu od punktu krytycznego V_(g) >>V_(c) , także objętość cieczy jest do zaniedbania w stosunku do objętości gazu, a para w tych warunkach spełnia w przybliżeniu równanie stanu gazu doskonałego. Przyjmując te założenia otrzymujemy równanie Clausiusa-Clapeyrona:

Lub

Po scałkowaniu, przy założeniu niezależności ciepła parowania od temperatury otrzymujemy:

Wykonanie pomiarów:

T [^0C]	T [K]	1/T =xi *10^-3	h1 [mmHg]	h2 [mmHg]	Δh [mmHg]	p=patm-Δh	lgp=yi	xiyi *10^-3	xi^2 *10^-5
23	296	3,378	685	86	599	169	2,228	7,527	1,141
27	300	3,333	644	100	544	224	2,350	7,834	1,111
31	304	3,289	662	115	547	221	2,344	7,712	1,082
35	308	3,247	651	130	521	247	2,393	7,768	1,054
39	312	3,205	640	144	496	272	2,435	7,803	1,027
43	316	3,165	620	166	454	314	2,497	7,902	1,001

Przykładowe obliczenia dla T=23⁰C

Ciśnienie odczytane na barometrze w laboratorium wynosi: 768mmHg

x_i =1/T

x_i=1/296=3,378*10^-3 [1/K]

Wysokość słupków cieczy manometrycznej przy pomiarach wynosi:

h₁=685mmHg

h₂=86mmHg

Δh=h₁-h₂=589-86=599mmHg

p=p_atm-Δh

p=768-599=169mmHg

y_i=lgp

y_i=lg169=2,228

x_iy_i=3,378*10^-3 *2,228=7,527*10^-3

x_i²=(3,378*10^-3 )²=1,141*10^-5[1/K²]

Wyliczam współczynnik a:

---