Michał Burski M-51

Sylwester Brygoła M-51

Określić zasób masy Δm powietrza traktowanego jako gaz doskonały który wypłynie z butli o zasobie objętości V=0,04[m³] przy ciśnieniu początkowym p₁=15[MPa] i temperaturze początkowej T₁=830,04[K] w przemianie adiabatycznej odwracalnej (izentropowej). Jaka będzie temperatura końcowa T₂ powietrza pozostałego w butli jeżeli ciśnienie otoczenia wynosi p₀=0,1[MPa], indywidualna stała gazowa R=287,04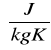
zaś wykładnik izentropy k=1,4

Dane: Szukane: Δm, T_2, m₀

V=0,04[m³]

p₁=15[MPa]=15000000 [Pa]

T₁=830,04[K]

p₀=0,1[MPa]= 100000[Pa]

R=287,04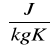

1. Schemat opróżniania butli z gazem

Początek opróżniania

p=p₁ T=T₁ m=m₁

Proces opróżniania

p₀<p<p₁ T₀<T<T₁ m₀<m<m₁

Koniec opróżniania

p=p₀ m=m₀

2. Wykresy przemian w układzie pV i Ts

3. Bilans zasobu energii wewnętrznej dla układu otwartego

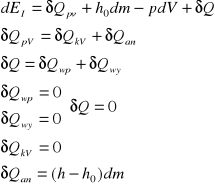
Przemiana adiabatyczna

V=const

Przemiana izochoryczna

dV=0

zatem bilans zasobu EW przyjmuje postać

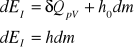
4. Wyznaczanie zasobu gazu w zbiorniku m₀ w chwili opróżnienia butli w układzie otwartym

Przyrost energii wewnętrznej w układzie otwartym jest równy

Bilans zasobu energii wewnętrznej po uporządkowaniu przyjmuje postać

Uwzględniając że masowa gęstość entalpii jest wyrażona zależnością

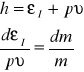
Biorąc pod uwagę równanie gazu doskonałego Clapeyrona

Równanie Meyera

c_p-c_v=R

Definicja wykładnicza izentropy

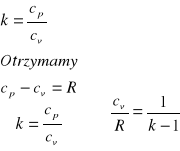
Równanie bilansu energii wewnętrznej przyjmuje postać

Całkując równanie w granicach

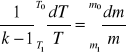
Otrzymamy

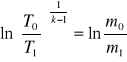
A stąd

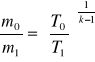
Uwzględniając równanie gazu doskonałego Clapeyrona możemy napisać

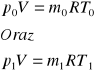
Dzieląc ostatnie związki stronami

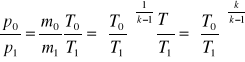
Mamy więc

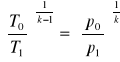
A stąd

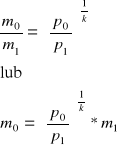
5. Wyznaczenie zasobu masy gazu który wypłyną ze zbiornika

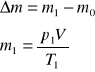
A stąd

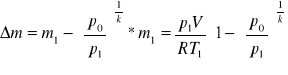
6. Wyznaczanie temperatury gazu w chwili końca wypływu ze zbiornika

uwzględniając zależność

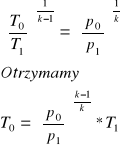
7. Obliczam wartości zasobu masy m₀ Δm i T₀

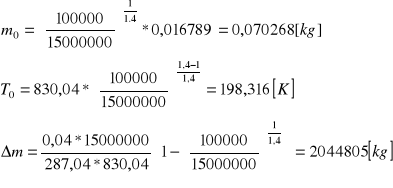
p₁

p₀

p

V

1

2

s₂

s₁

T

s

ΔQ_pV

V=const

Osłona adiabatyczna

p

T

dm

---