1.Wskaznik uwarunkowania macierzy

Wskaźnik uwarunkowania macierzy A w równaniu Ax = b jest charakterystyczną własnością macierzy informującą o tym jakie wzmocnienie będzie miała zmiana normy macierzy A na normę rozwiązania x.

Wskaźnik uwarunkowania macierzy definiuje się bardziej precyzyjnie jako maksymalny stosunek błędu względnego wektora rozwiązania x do błędu względego b

Liczymy go poleceniem np cond(A)

Macierz diagonalna

Macierz, zwykle kwadratowa[1], której wszystkie współczynniki leżące poza główną przekątną (główną diagonalą) są zerowe. Inaczej mówiąc jest to macierz górno- i dolnotrójkątna jednocześnie.

Macierz ortogonalna

To macierz kwadratowa spełniająca równość:

Innymi słowy, macierz jest ortogonalna, jeśli jej macierzą odwrotną jest macierz do niej transponowana. Macierz ortogonalna to macierz unitarna o wyrazach rzeczywistych.

Metoda Jacobiego

Metoda Jacobiego jest metodą iteracyjną i pozwala nam obliczyć układ n równań z n niewiawiadomymi Ax = b. Wektor x0 będący początkowym przybliżeniem rozwiązania układu będzie dany (zwykle przyjmuje się go jako wektor złożony z samych zer). Kolejne przybliżenia będziemy obliczać według następującego wzoru:

xn+1 = Mxn + Nb,

Obliczymy następujący układ równań:

4x1 - x2 - 0.2x3 + 2x4 = 30

-1x1 + 5x2 - 2x4 = 0

0.2x1 + x2 + 10x3 - x4 = -10

- 2x2 - x3 + 4x4 = 5

Zapiszmy go teraz w postaci Ax = b

Podzielmy teraz macierz A na sumę macierzy L + D + U

Obliczmy teraz macierz N = D-1

A teraz kolejno M = -D-1(L+U) = -N(L+U).

Rozpoczynamy od zerowego przybliżenia czyli x10 = 0, x20 = 0, x30 = 0, x40 = 0

Obliczmy pierwszą iterację metody, według przytoczonego na początku wzoru:

x11 = 7,5 + 0,25x20 + 0,05x30 - 0,5x40

x11 = 7,5

x21 = 0 + 0,2x10 + 0,4x40

x21 = 0

x31 = -1 - 0,02x10 - 0,1x20 + 0,1x40

x31 = -1

x41 = 1,25 + 0,5x20 + 0,25x30

x41 = 1,25

Kolejna iteracja

x12 = 7,5 + 0,25x21 + 0,05x31 - 0,5x41

x12 = 6,825

x22 = 0 + 0,2x11 + 0,4x41

x22 = 2

x32 = -1 - 0,02x11 - 0,1x21 + 0,1x41

x32 = -1,025

x42 = 1,25 + 0,5x21 + 0,25x31

x42 = 1

Można teraz obliczyć kolejną iterację. Każda z nich przybliża nas do dokładnego wyniku.

Metoda Gaussa-Seidla

Dana jest funkcja f ( x1, x2) . Poszukiwane jest minimum tej funkcji w z żądaną

dokładnością  z krokiem k . Punkt startowy ( x01, x02) .

Minimalizacja funkcji celu odbywa się wzdłuż kolejnych kierunków bazy ortogonalnej

utworzonej z wersorów układu kartezjańskiego: ei , gdzie i=1, ... n , n - liczba zmiennych

- dla rozpatrywanego przypadku n=2 (podczas obliczeń baza ta nie ulega zmianie).

Minimalizacja wzdłuż kolejnych kierunków wykonywana jest przy zastosowaniu metod

optymalizacji dla funkcji jednej zmiennej.

Algorytm

Krok 1

Podstawić i=1

Krok 2

Obliczyć minimum funkcji celu w kierunku e1

● podstawić do funkcji celu za zmienną x2 wartość x02 (w pierwszej iteracji x02 to

współrzędna punktu startowego, w kolejnych - współrzędna punktu z poprzedniej

iteracji)

● funkcję celu minimalizować jako funkcję jednej zmiennej z dokładnością p i

krokiem k

Krok 3

Podstawić i=2

Krok 4

Obliczyć minimum funkcji celu w kierunku e2

● podstawić do funkcji celu za zmienną x1 wartość x01 (w pierwszej iteracji x01 to

współrzędna punktu startowego, w kolejnych - współrzędna punktu z poprzedniej

iteracji)

● funkcję celu minimalizować jako funkcję jednej zmiennej z dokładnością p i

krokiem k

Metoda potęgowa

PRZYKŁAD

1)Niech będzie dana macierz:

W celu obliczenia wektora własnego wybieramy wektor startowy

OSTATECZNIE

obliczony wektor własny

Obliczona wartość własna λ= -2

2)Niech będzie dana macierz

Wybieramy wektor startowy

OSTATECZNIE

obliczony wektor własny

Obliczona wartość własna λ= 4

Metoda potęgowa

Interpolacja - metoda numeryczna polegająca na wyznaczaniu w danym przedziale tzw. funkcji interpolacyjnej, która przyjmuje w nim z góry zadane wartości w ustalonych punktach, nazywanych węzłami. Stosowana jest ona często w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami oraz w celu uproszczenia skomplikowanych funkcji, np. podczas całkowania numerycznego. Interpolacja jest szczególnym przypadkiem metod numerycznych typu aproksymacja.

Macierz Vandermonde'a - macierzą kwadratową n x n postaci:

Efekt Rungego - pogorszenie jakości interpolacji wielomianowej, mimo zwiększenia liczby jej węzłów. Początkowo ze wzrostem liczby węzłów n przybliżenie poprawia się, jednak po dalszym wzroście n zaczyna się pogarszać, co jest szczególnie widoczne na końcach przedziałów.

Interpolacja funkcjami sklejanymi stopnia trzeciego

Główną cechą wyróżniającą interpolację funkcjami sklejanymi, jest podział

przedziału, na którym znajdują się węzły, na mniejsze podprzedziały a następnie użycie

na każdym z nich wielomianu interpolacyjnego odpowiednio niskiego stopnia (u nasdokładnie trzeciego).

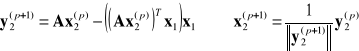
• Jeżeli x_i^(p+1)/x_i^(p) różnią się o mniej niż zadana dokładność dla każdego i, kończymy iterację. Wtedy x^(p) jest szukanym wektorem własnym a wielkość jest przybliżeniem wartości własnej o największym module.

W ten sposób można też znaleźć kolejne wartości i wektory własne. Po znalezieniu pierwszego wektora własnego tworzymy wektor do niego ortogonalny i prowadzimy ortogonalizując za każdym razem otrzymany wektor do pierwszego wektora własnego. Przykładowo, dla drugiego wektora własnego:

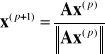
• Wybieramy przybliżenie początkowe wektora własnego odpowiadającego wartości własnej o największym module.

• Kolejne przybliżenie wektora własnego obliczamy z wzoru:

Metoda potęgowa (iteracji wektorów)

---