Andrzej Iwasiewicz
Akademia Ekonomiczna
w Krakowie
Karty kontrolne Shewharta
jako narzędzie statystycznego sterowania procesami
1. Wprowadzenie
Karty kontrolne (ang. control charts) są podstawowymi i najwcześniejszymi historycznie narzędziami statystycznego sterowania procesami. Idea karty kontrolnej pochodzi od Waltera A.Shewharta (1891-1967).
Pierwsza jego publikacja na ten temat ukazała się w roku 1926 [14], a pierwsze praktyczne zastosowanie karty kontrolnej miało miejsce dwa lata wcześniej, 16 maja 1924 [8] w zakładach Western Electric (USA). Pomysł karty kontrolnej był reakcja na zagrożenia wynikające z powiększającego się się dystansu miedzy produkcyjnymi i kontrolnymi możliwościami człowieka. Wydajne i ciągle doskonalone urządzenia technologiczne pozwalały bardzo szybko zwiększać wielkość produkcji, natomiast możliwości człowieka w zakresie kontroli i oceny jakości wytwarzanych produktów pozostawały na poziomie charakterystycznym dla produkcji rzemieślniczej. Stanowiło to bardzo istotne zagrożenie dla jakości masowo wytwarzanych produktów. W.A.Shewhart dostrzegł to zagrożenie i zaproponował wyposażenie systemów produkcyjnych w instrumenty formalne, które zwielokrotniły potencjał kontrolny tych systemów, a jednocześnie stworzyły realne możliwości sterowania nimi, w celu osiągnięcia założonego poziomu jakości. Podstawowym elementem owego instrumentarium była karta kontrolna, pomyślana jako graficzny algorytm wykrywania rozregulowań obserwowanego procesu. Drugim, równie ważnym, elementem był algorytm wykorzystywania sygnałów emitowanych przez kartę kontrolna do eliminacji przyczyn rozregulowania. Propozycje W.A.Shewharta zostały przyjęte z rezerwą, a ich szerokie zastosowanie stało się faktem dopiero w latach drugiej wojny światowej, w okresie wzmożonego wysiłku produkcyjnego amerykańskiego przemysłu. W późniejszych latach karty kontrolne Shewharta stały się standardowym narzędziem statystycznego sterowania procesami, a jednocześnie były one przedmiotem intensywnych badań. Doprowadziło to do wielu udoskonaleń pierwotnej koncepcji, a na przełomie lat pięćdziesiątych i sześćdziesiątych pojawił nowy typ kart kontrolnych, a mianowicie karty kontrolne sum skumulowanych (ang.cum-sum charts). Pionierskie znaczenie miały tu prace E.S. Page'a [13], G.A. Barnarda [1],[2], W.D. Evana [4] i K.W.Kempa [9].
2. Formułowanie wymagań jakościowych dla potrzeb sterowania procesem
Warunkiem racjonalnego wykorzystania karty kontrolnej w systemie sterowania procesem jest precyzyjne określenie wymagań jakościowych stawianych produktowi, albo procesowi. Najczęściej wykorzystuje się do tego celu dwie miary jakości wykonania, a mianowicie
wadliwość (ang. fraction defective, percentage defective), albo
liczbę wad w jednostce produktu (ang. defects per unit) lub liczbę wad na sto jednostek produktu (ang. defects per hundred units).
Wymagania w zakresie jakości wykonania formułowane są przez podanie największej dopuszczalnej wartości jednej z tych miar, a wiec albo przez podanie największej dopuszczalnej wadliwości produktu, albo przez określenie największej dopuszczalnej przeciętnej liczby wad w elementarnej lub agregatowej jednostce produktu.
Nowa norma terminologiczna PN-ISO 3534-2 [17] dokonała pewnych zmian w zakresie zalecanych miar jakości wykonania. Dokonano rozróżnienia miedzy wadą i niezgodnością. W konsekwencji, w miejsce wadliwości zalecane są obecnie następujące miary:
frakcja jednostek niezgodnych (ang. proportion of nonconforming items; units)
procent jednostek niezgodnych (ang. percentage of nonconforming items; units)
frakcja jednostek wadliwych (ang. proportion of defectives items; units
procent jednostek wadliwych (ang. percentage of defectives items; units)
Analogicznie, w miejsce drugiej spośród wymienionych powyżej miar jakości wykonania, norma PN-ISO 3534-2 zaleca używanie następujących miar:
liczba niezgodności na jednostkę produktu (ang. nonconformities per item)
liczba niezgodności na sto jednostek produktu (ang. nonconformities per hundred items)
liczba wad na jednostkę produktu (ang. defects per item)
Należy tez wymienić jeszcze jedna miarę, jaką jest
liczba wad na sto jednostek produktu (ang. defects per hundred items)
Wzmiankowana norma nie wymienia tej miary. Nie zmienia to jednak faktu, ze może ona być lepiej uwarunkowana numerycznie niż liczba wad na jednostkę produktu, albowiem wady pojawiają się rzadko (rzadziej niż niezgodności) i w związku z tym wygodniej odnosić ich liczbę do większej umownej jednostki produktu.
W dalszych rozważaniach nie będziemy rozróżniać niezgodności i wad, albowiem rozróżnienie to nie ma żadnego wpływu na konstrukcje i funkcjonowanie kart kontrolnych. Pozostaniemy przy pojęciu wadliwości produktu oraz przy pojęciu liczby wad w rzeczywistej lub umownej jednostce produktu. Będziemy przy tym pamiętać, że pojęcia te można zawsze i bez jakichkolwiek komplikacji zastąpić wymienionymi powyżej miarami, zalecanymi przez PN-ISO 3534-2.
Wadliwość można interpretować zarówno jako frakcje, jak i jako prawdopodobieństwo. W odbiorczych badaniach jakości bardziej czytelne jest pojecie frakcji, albowiem przedmiotem badania jest wówczas jakość produktu reprezentowanego przez pewien skończony zbiór jego jednostek, czyli tak zwana partię. W przypadku sterowania jakością w toku produkcji pojęcie frakcji staje się mniej użyteczne, albowiem operujemy tu strumieniami, a nie partiami produktu. Strumień jest uporządkowanym w czasie ciągiem jednostek produktu. Wygodniejszą miarą jakości wykonania jest tu prawdopodobieństwo zdarzenia losowego polegającego na tym, ze proces wygeneruje jednostkę produktu nie spełniającą stawianych jej wymagań jakościowych. Istota sterowania procesem kreowania jakości polega na takim oddziaływaniu na jego wejścia, by to prawdopodobieństwo było jak najmniejsze, a przynajmniej nie większe niż pewna wartość uzgodniona miedzy producentem a odbiorca produktu.
Wadliwość produktu ze względu na zmienna diagnostyczna X oznaczymy symbolem p i zdefiniujemy ja następująco:
p = P(x X ) (1)
gdzie x jest realizacja obserwowanej zmiennej diagnostycznej X w jednostce produktu, natomiast X jest podzbiorem niepożądanych wartości zmiennej X. Podzbiór ten otrzymujemy w rezultacie rozcięcia zbioru wartości zmiennej X, który oznaczymy symbolem X , na podzbiór wartości pożądanych X oraz podzbiór wartości niepożądanych X. Rozcięcie to należy przeprowadzić w taki sposób, by
X X = X (2)
i by jednocześnie
X X = (3)
W teorii i w praktyce statystycznego sterowania procesami kreowania jakości wykorzystuje się dwa typy zmiennych diagnostycznych, a mianowicie
zmienne zerojedynkowe, a także
zmienne ciągle, wśród których podstawowa role odgrywają zmienne losowe o normalnym rozkładzie prawdopodobieństwa.
Zmienne zerojedynkowe stosowane są w przypadku alternatywnej oceny właściwości i są one definiowane następująco:
0 gdy jednostka produktu spełnia wymagania jakościowe
X = (4)
1 gdy jednostka produktu nie spełnia wymagań jakościowych
W takiej sytuacji mamy:
p = P(X = 1) = P(X 0) (5)
albowiem X = {0;1}, X = {0}, X = {1}.
Ciągłe zmienne diagnostyczne stosowane są w przypadku tak zwanej liczbowej oceny właściwości. To nieco enigmatyczne określenie, utrwalone już w systemie norm PN, oznacza, ze pomiar natężenia właściwości odbywa się na skali co najmniej przedziałowej. W przypadku ciągłych zmiennych diagnostycznych zbiór wartości pożądanych X przybiera postać przedziału liczbowego na osi badanej zmiennej, nazywanego przedziałem tolerancji. Przedział ten będziemy oznaczać symbolem Xo. W przedziale tolerancji wyróżnia się często wartość optymalna (najbardziej pożądana) xo Xo. Przedział tolerancji może być ograniczony obustronnie
Xo = [xd ;xg ] (6)
albo tylko jednostronnie
Xo = [a ;xg ] (7)
Xo = [xd ;b ] (8)
Wartości a i b nie są tu ograniczeniami w sensie wymagań jakościowych. Są one uwarunkowane formalnymi własnościami przyjętej skali pomiarowej, albo nawet technicznymi własnościami zastosowanego instrumentarium pomiarowego. Jeśli - na przykład - badaniu podlega procentowe stężenie jakiegoś składnika w produkcie, to a = 0%, b = 100%. Tak wiec, jeśli przedział tolerancji ograniczony jest obustronnie to
p = P(x Xo ) = P(x < xd ) + P(x > xg ) (9)
W przypadku przedziału tolerancji ograniczonego tylko prawostronnie mamy
p = P(x Xo ) = P(x > xg ) (10)
Jeśli natomiast przedział tolerancji ograniczony jest tylko lewostronnie, to wówczas
p = P(x Xo ) = P(x < xd ) (11)
Mając wartość p charakterystyczną dla danego procesu można ocenić jego wydolność, a następnie - jeśli proces okaże się wydolny - skonstruować operacyjne definicje stanu uregulowania i stanu rozregulowania tego procesu. Problemy związane z ocena wydolności procesu omówiono szerzej w pracy [7]. Przypomnijmy tu tylko, że ocena taka musi być przeprowadzona przed przystąpieniem do operacyjnego sterowania procesem za pomocą kart kontrolnych. Należy wszak pamiętać, że jeśli proces jest niewydolny, to podjecie operacyjnego sterowania nie może zapewnić pożądanego poziomu jakości. O ile wydolność procesu jest jego ogólna właściwością, o tyle stan uregulowania i stan rozregulowania należy definiować w odniesieniu do konkretnego punktu na osi czasu.
Obserwowany proces należy uważać za uregulowany w chwili t, jeśli zachodzi nierówność
pt po (12)
gdzie pt jest wadliwością produktu (procesu) w chwili t, natomiast po oznacza przyjęta dla potrzeb sterowania, największa dopuszczalna wadliwością produktu ze względu na zmienna diagnostyczna X. Wartość po powinna być co najwyżej równa wartości p'o zastosowanej przy badaniu wydolności procesu (po p'o). Należy tu dodać, p'o jest istotnym elementem umów miedzy producentem a odbiorcami produktu, natomiast po jest wartością wykorzystywaną tylko w procesie sterowania.
Jeśli zachodzi nierówność
pt > po (13)
to obserwowany proces produkcyjny jest rozregulowany w chwili t.
Przedstawione powyżej rozumowanie można powtórzyć w całości i bez żadnych istotnych modyfikacji w odniesieniu do drugiej miary jakości wykonania, a mianowicie przeciętnej liczby wad w jednostce produktu. Obserwowany proces jest uregulowany w chwili t, jeśli spełniona jest nierówność
t (14)
gdzie t oznacza rzeczywista przeciętna liczbę niezgodności (wad) ze względu na zmienną diagnostyczną X, w ustalonej jednostce produktu, natomiast o jest największa dopuszczalna wartością tej charakterystyki, ustalona dla potrzeb sterowania procesem.
Proces jest rozregulowany w chwili t, jeśli zachodzi nierówność
t > (15)
Wartość o , podobnie jak po , jest ważnym elementem normy jakości wykonania (zob. rys.1). Analogicznie jak w przypadku wadliwości powinna być spełniona nierówność o `, w której 'o oznacza największa dopuszczalną liczbę niezgodności (wad) w jednostce produktu, uwzględnioną podczas badania wydolności procesu i będąca rezultatem umowy miedzy producentem i odbiorcą produktu.
3. Funkcjonowanie karty kontrolnej w systemie sterowania procesem
Rolę i funkcjonowanie karty kontrolnej w systemie sterowania procesem ilustruje rys.1. System pokazany na tym rysunku jest układem względnie odosobnionym i można w nim wyróżnić dwa podsystemy, a mianowicie
podsystem wytwórczy, oraz
podsystem kontroli i regulacji.
Podsystem wytwórczy składa się z agregatu produkcyjnego i operatora tego agregatu. Podsystem ten jest zasilany z otoczenia strumieniami mediów niezbędnych do jego funkcjonowania (surowce, materiały, energia i informacje technologiczne), natomiast generuje on strumień produktu. Strumień ten powinien reprezentować odpowiednio wysoki poziom jakości, uzgodniony z odbiorcą. W tym celu należy zorganizować pętle ujemnego sprzężenia zwrotnego miedzy strumieniem produktu, a agregatem generującym ten strumień. W systemie pokazanym na rys.1 pętla ta składa się z bloku pomiarowego i bloku analizującego, a także odpowiednich strumieni. Karta kontrolna zainstalowana jest w bloku analizującym. Jej zadaniem jest rozstrzyganie, czy stwierdzone w danym momencie odchylenie od zadanej normy jakości wykonania można traktować jako przypadkowe (losowe), czy też jest to odchylenie systematyczne, którego nie można wyjaśnić działaniem przyczyn losowych. Informacje dotyczące normy jakości wykonania (po , o , xo ) wprowadzane są do bloku analizującego (zob. rys.1) przez kierownictwo wyższego szczebla. Jeśli karta kontrolna wykryje systematyczne odchylenie od zadanej normy jakości wykonania, to następuje emisja sygnału o rozregulowaniu procesu. Jest to pierwszy krok w cyklu działań zmierzających do wykrycia rzeczywistej przyczyny rozregulowania procesu. W literaturze przedmiotu działania te określane są jako cykl Shewharta [5],[10]. Schemat tego cyklu pokazano na rys.2. W pracach W.A. Shewharta, a w konsekwencji również w całej angielskojęzycznej literaturze przedmiotu, owa systematyczna (nielosowa) przyczyna rozregulowania określana jest jako "assignable cause", czyli jako przyczyna wyznaczalna. Takie właśnie wierne, ale niezbyt fortunne tłumaczenie tego terminu przyjęto w nowej normie terminologicznej PN-ISO 3534-2 [17]. W świetle zwyczajów językowych zakorzenionych w polskiej literaturze statystycznej należy raczej mówić o przyczynie systematycznej, albo - jak zaleca Słownik jakości [15] - o przyczynie nielosowej. Dodajmy, że odpowiedni termin francuskojęzyczny brzmi "cause systematique". Karta kontrolna może tez być wykorzystana w znacznie skromniejszym zakresie, jako element analizujący w systemach regulacji automatycznej. W takiej sytuacji blok analizujący musi być wyposażony w układ wyznaczający wielkość poprawki jaką należy wprowadzić na odpowiednie wejście agregatu produkcyjnego. Decyzje podejmowane przy użyciu karty kontrolnej oparte są na analizie informacji dostarczanych przez próbki losowe pobierane ze strumienia produktu. Są to wiec badania nie wyczerpujące. Ma to ten skutek, że podejmowane decyzje mogą być obciążone dwojakiego rodzaju błędami, które w teorii weryfikacji hipotez statystycznych określane są jako błędy pierwszego rodzaju i błędy drugiego rodzaju. Przypomnijmy [3], że błąd pierwszego rodzaju polega na odrzuceniu prawdziwej hipotezy zerowej, a prawdopodobieństwo popełnienia tego błędu oznaczane jest symbolem . W odniesieniu do rozważanych tu problemów błędem pierwszego rodzaju jest wiec zakwalifikowanie procesu przebiegającego prawidłowo jako procesu rozregulowanego i (w konsekwencji) podjęcie działań regulacyjnych. Tak wiec, symbolem będziemy oznaczać prawdopodobieństwo zbędnej regulacji procesu. Błąd drugiego rodzaju polega na zaakceptowaniu (przyjęciu) fałszywej hipotezy zerowej, a prawdopodobieństwo popełnienia tego błędu oznaczane jest symbolem . W rozważanej sytuacji błędem drugiego rodzaju jest wiec nie podjecie działań regulacyjnych, gdy są one konieczne.
4. Konstrukcja i funkcjonowanie kart kontrolnych typu Shewharta
Głównym elementem każdej karty kontrolnej jest diagram przeglądowy, czyli wykres służący do monitorowania procesu. W przypadku kart kontrolnych typu Shewharta diagram ten ma postać przedstawiona schematycznie na rys.3. Na osi poziomej, oznaczonej symbolem t, odkłada się numer kolejnej próbki pobranej do badania ze strumienia produktu (zob. rys.1), albo numer kolejnego przedziału próbkowania wyróżnionego na osi czasu rzeczywistego. Na osi pionowej odkłada się natomiast wartości obserwowanej charakterystyki z próbki (t). Charakterystyka ta jest funkcja postaci
t = (Xt) (16)
gdzie
X = { xt.1 ,x t.2 ,...,xt.i,...,xt.n } (17)
oznacza zbiór wartości zmiennej diagnostycznej X, zrealizowanych w próbce o numerze t. Kolejne zbiory Xt są elementami strumienia generowanego przez blok pomiarowy w systemie pokazanym na rys.1. W szczegółowych rozwiązaniach obserwowana charakterystyka z próbki może być, na przykład, średnia arytmetyczna z próbki (wówczas t = ![]()
), odchylenie standardowe z próbki (wówczas t = st ), czy liczba sztuk wadliwych (niezgodnych) stwierdzona w próbce (wówczas t = zt ). Niezależnie od zastosowanego szczegółowego rozwiązania, charakterystyka t jest zmienną losową o rozkładzie prawdopodobieństwa zależnym od rozkładu zmiennej diagnostycznej X, oraz od liczności próbki (n). Ważnym elementem diagramu przeglądowego jest tak zwana linia centralna (ang. center line, CL). Linię tę wykreśla się równolegle do osi t, na poziomie . Jest taka wartość charakterystyki z próby, przy której p = po , albo , w zależności od tego, która miara jakości wykonania jest używana w konkretnym przypadku. Linia centralna jest układem odniesienia dla kolejnych wartości t . Jest to także układ odniesienia dla linii kontrolnych; zarówno dla tych, które pełnią funkcje granic regulacji (ang. control limits), jak i dla tych, które wykorzystywane są do innych celów. W zależności od potrzeb konkretnego badania stosuje się dwustronny albo jednostronny schemat kontrolny. Schemat dwustronny stosuje się przede wszystkim wówczas, gdy badana zmienna diagnostyczna X jest ciągła, a przedział tolerancji jest ograniczony obustronnie; zob. wzór (6). W takiej sytuacji na diagramie przeglądowym wykreśla się zarówno górną jak i dolną granicę regulacji (ang. upper control limit, UCL; lower control limit, LCL). W jednostronnych schematach kontrolnych niezbędna jest tylko jedna granica regulacji. Najczęściej stosowany jest prawostronny schemat kontrolny. W schemacie tym podstawowe znaczenie ma górna linia kontrolna, a linia dolna (jeśli jest wykreślana) odgrywa rolę pomocniczą i nie jest ona granicą regulacji. Linia ta służy do wykrywania objawów postępu technologicznego; biernego albo wymuszonego działaniami w sferze prewencji. Odwrotną sytuację mamy w rzadko stosowanym lewostronnym schemacie kontrolnym. Podstawową rolę odgrywa tu dolna linia kontrolna, albowiem rozregulowanie procesu (w sensie pogorszenia jakości) może się przejawić tylko poprzez nadmierne obniżenie się wartości obserwowanej charakterystyki z próby t. Górna linia kontrolna (jeśli jest wykreślana) nie jest granicą regulacji. Służy ona, analogicznie jak dolna linia kontrolna w prawostronnym schemacie kontrolnym, do wykrywania korzystnych zmian w procesie. Szczegółowe równania linii kontrolnych podamy w punktach 5, 6 i 7 przy omawianiu poszczególnych typów kart kontrolnych. Obecnie zauważmy tylko, że linie te wykreśla się w takiej odległości od linii centralnej, by prawdopodobieństwo losowego ich przekroczenia - w przypadku gdy pt = po , albo t - było bardzo małe. Jest to wspomniane powyżej prawdopodobieństwo zbędnej regulacji procesu . W większości przypadków przyjmuje się, że obserwowana charakterystyka z próby jest zmienną losową o normalnym rozkładzie prawdopodobieństwa. Przyjmuje się wiec, że ~ N[(,σ()]. W takiej sytuacji położenie granic regulacji ustala się według podanych poniżej ogólnych reguł. W przypadku dwustronnego schematu kontrolnego mamy:
g = o + u/2σ( (18)
d = o - u/2σ( (19)
gdzie ua/2 jest taką wartością standaryzowanej normalnej zmiennej losowej U ~ N(0;1), że
P(U > u/2) = /2 (20)
przy czym , analogicznie jak powyżej, oznacza prawdopodobieństwo zbędnej regulacji procesu.
Jeśli mamy do czynienia z prawostronnym schematem kontrolnym, to wówczas
g = o + u σ( (21)
W przypadku lewostronnego schematu kontrolnego mamy natomiast
d = o - u σ( (22)
W obu tych wzorach u jest taką wartością standaryzowanej normalnej zmiennej losowej U ~ N(0;1), że
P(U > u) = (23)
W analogiczny sposób można wyznaczyć wspomniane powyżej linie kontrolne nie będące granicami regulacji, a służące do wykrywania objawów postępu technologicznego. W odniesieniu do prawostronnego schematu kontrolnego mamy
d = o - u σ( (24)
natomiast w przypadku schematu lewostronnego linia ta ma następujące równanie
g = o + u σ( (25)
W równaniach tych u ma taką samą interpretację jak u w równaniach (21) i (22), przy czym nie jest prawdopodobieństwem zbędnej regulacji, lecz prawdopodobieństwem pojawienia się fałszywego sygnału o korzystnych zmianach w obserwowanym procesie.
Kwantyle u , u i u można wyznaczyć na podstawie stablicowanych wartości dystrybuanty zmiennej losowej U ~ N(0;1), albo wprost odczytać z odpowiedniej tablicy wartości krytycznych testu u, albo testu t, dla nieskończenie dużej liczby stopni swobody. Tablice takie zamieszczone są w niemal każdym podręczniku statystyki; zob. na przykład [3].
U podstaw przedstawionej metody wyznaczania linii kontrolnych leży fakt, że karty kontrolne Shewharta są w istocie odpowiednio zorganizowanymi sekwencjami klasycznych testów istotności. Tego oczywistego faktu nie respektują ortodoksyjni zwolennicy poglądów W.A. Shewharta. Stoją oni na stanowisku, ze - zgodnie z pierwotnymi propozycjami W.A. Shewharta - należy zawsze stosować tak zwane trójsigmowe granice regulacji. Równania tak rozumianych linii kontrolnych przedstawiają się następująco:
g = o + 3 σ( (26)
d = o - 3 σ( (27)
Z właściwości rozkładu normalnego wynika, że:
P[ ( σ( = P[ > ( σ( 0.0013
Tak wiec, w przypadku jednostronnych schematów kontrolnych mamy zawsze 0.0013 (0.13%), natomiast w dwustronnym schemacie kontrolnym mamy zawsze 2 * 0.0013 = 0.0026 (0.26%) [3]. Idea trójsigmowych granic regulacji jest bardzo mocno zakorzeniona w amerykańskiej literaturze przedmiotu. Koncepcja ta przeniknęła również do norm międzynarodowych [16], mimo że jej logiczne uzasadnienie jest bardzo problematyczne. Zjawisko to można wytłumaczyć tylko siłą tradycji. W połowie lat dwudziestych kończącego się stulecia, kiedy to pojawiła się koncepcja kart kontrolnych, teoria statystycznych testów istotności stawiała pierwsze kroki. Przypomnijmy, że podstawy teoretyczne tych testów są wspólnym dziełem Jerzego Spławy - Neymana (1894 - 1981) oraz Egona S. Pearsona (1895 - 1980). Teoria ta powstawała niemal równolegle z pracami W.A. Shewharta nad konstrukcją kart kontrolnych. Należy wiec przypuszczać, że w sytuacji gdy nie można było oczekiwać znajomości teorii testów istotności przez użytkowników kart kontrolnych, W.A. Shewhart był zmuszony do zaproponowania prostej i skutecznej metody wyznaczania granic regulacji, opartej na właściwościach formalnych rozkładu normalnego. Obecnie te uwarunkowania już nie działają. Podstawy statystyki matematycznej są obecnie integralnym elementem wykształcenia każdego ekonomisty i inżyniera. Dlatego też, nie należy - jak się wydaje - bezkrytycznie stosować zaleceń sprzed siedemdziesięciu lat. Nie należy tego czynić tym bardziej, że odstąpienie od trójsigmowych granic regulacji na rzecz wyznaczania granic regulacji w oparciu o wybrane prawdopodobieństwo zbędnej regulacji procesu () może być bardzo użyteczne praktycznie. Dodajmy, ze potrzeby praktyki przemysłowej wymusiły już dawno pewne odstępstwa od reguły trzech sigm. Na diagramie przeglądowym niekiedy wykreśla się dodatkowo, obok zewnętrznych linii kontrolnych (ang. outer control limit), również wewnętrzne linie kontrolne (ang. inner control limit), nazywane często granicami ostrzegawczymi (ang. warning limit). W ujęciu klasycznym przy wyznaczaniu tych linii stosuje się regułę dwóch sigm.
Mamy wiec:
'g = o + 2 σ( (28)
'd = o - 2 σ( (29)
gdzie 'g jest górną wewnętrzną linią kontrolną (ang. upper warning limit, UWL), natomiast 'd oznacza dolną wewnętrzną linię kontrolną (ang. lower warning limit, LWL). W ujęciu ogólnym położenie wewnętrznych linii kontrolnych wyznacza się według równań postaci (18) i (19) oraz (21) i (22), przyjmując prawdopodobieństwo fałszywego sygnału ostrzegawczego na poziomie ' > . Wszystkie przedstawione powyżej uwagi na temat wyznaczania położenia linii centralnej i linii kontrolnych dotyczą tak zwanej projektowej metody instalowania kart kontrolnych w systemach sterowania procesami; zob. rys. 1. W metodzie tej, jak to pokazano powyżej, położenie linii centralnej i linii kontrolnych wyznacza się na podstawie informacji zawartych w projekcie produktu i procesu, a sama karta kontrolna służy do wykrywania odstępstw od tego projektu. Istnieje również inna technika instalowania kart kontrolnych, określana jako metoda stabilizacyjna [11]. Rolą karty kontrolnej nie jest wówczas utrzymywanie zgodności miedzy projektem a wytwarzanym produktem, lecz stabilizacja jakości wykonania na zastanym poziomie (stad nazwa metody) i ewentualne późniejsza poprawa jakości produktu poprzez wykrywanie objawów postępu technologicznego i odpowiednia korektę (rewizję) granic regulacji. W przypadku stosowania tej metody, w pierwszym etapie instalowania karty kontrolnej prowadzi się badania procesu w celu oszacowania parametrów rozkładu zmiennej diagnostycznej X, a w dalszej kolejności oszacowania parametrów obserwowanej charakterystyki z próby (). Linię centralną wykreśla się wówczas na poziomie średniej arytmetycznej
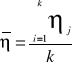
(30)
gdzie j oznacza wartość charakterystyki uzyskana w j-tej próbce, natomiast k jest liczbą próbek o ustalonej liczności, pobranych ze strumienia produktu (zob. rys.1) podczas wstępnego badania procesu. Na podstawie wyników badania tych samych próbek wyznacza się również odchylenie standardowe
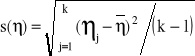
(31)
będące oszacowaniem nie znanej wartości σ(). Mając te wartości można wyznaczyć linie centralną i linie kontrolne według podanych powyżej wzorów, podstawiając o = ![]()
i σ() = s(). W dalszych rozważaniach nie będziemy omawiać stabilizacyjnej metody instalowania kart kontrolnych. Rozważania te poświecimy w całości kartom kontrolnym instalowanym według informacji normatywnych. W nowoczesnych systemach zarządzania jakością jest to metoda podstawowa.
Na diagram przeglądowy z wykreśloną linią centralną i liniami kontrolnymi, a także - w miarę potrzeby - również wewnętrznymi liniami kontrolnymi, nanosi się kolejne punkty (t; t); t = 1,2,.... Problem ten ilustruje rys. 3, na którym przedstawiono funkcjonowanie dwustronnego schematu kontrolnego. W rozważanym przypadku obserwowany proces uważa się za uregulowany, jeśli punkty (t; t) rozkładają się losowo wokół linii centralnej (o), a jednocześnie żaden z nich nie wykracza poza linie kontrolne; zob. punkty (1;1) i (2; 2) na rys.3. Jeśli pojedynczy punkt (t;t) wykracza poza linię kontrolną (górną albo dolną), to mamy do czynienia z sygnałem punktowym; zob. punkty (3;3 ) i (4; 4) na rys.3. Jest to najprostszy i podstawowy typ sygnału o rozregulowaniu procesu. Nie jest to jednak jedyny typ sygnału, jaki może wyemitować karta kontrolna typu Shewharta. Sygnałami są także pewne konfiguracje punktów (t;t) z których żaden (traktowany z osobna) nie przemawia za tym, że obserwowany proces jest rozregulowany. Przykładem takiego sygnału jest sześcioelementowa sekwencja punktów (5; 5),...,(10; 10); zob. rys.3. Wszystkie te punkty leżą powyżej linii centralnej (o), a jednocześnie żaden z nich nie wykracza poza górną linię kontrolną (g). Jeśli proces jest uregulowany, to oczywiście można uzyskać taka konfiguracje kolejnych punktów, ale prawdopodobieństwo takiego zdarzenia jest bardzo małe. Jeśli rozkład zmiennej losowej t jest symetryczny, to prawdopodobieństwo to wynosi (1/2)2 = 1/64 0.016. Jeśli zatem w toku postępowania uzyskamy konfigurację przedstawioną na rysunku, to mamy prawo odrzucić przyjęte wstępnie założenie, ze proces jest uregulowany i podjąć działania zmierzające do znalezienia systematycznej przyczyny zakłócającej obserwowany proces. Przedstawiony powyżej sygnał określany jest jako sygnał seryjny, albo sekwencyjny. W normie ISO 8258 [16], przedstawiono osiem różnych konfiguracji punktów (t; t), które traktowane są jako sygnały o rozregulowaniu obserwowanego procesu.
5. Przykłady kart kontrolnych typu Shewharta stosowanych przy liczbowej ocenie właściwości.
Wśród kart kontrolnych stosowanych w przypadku liczbowej oceny właściwości produktu lub procesu podstawową rolę dogrywa karta kontrolna ![]()
. Jest ona nazywana kartą kontrolną x - średnie, albo karta kontrolna x z kreską (ang. x - bar chart). Kartę tę można stosować wówczas, gdy badana zmienna diagnostyczna X jest zmienną losową o normalnym rozkładzie prawdopodobieństwa, a odchylenie standardowe tej zmiennej (σ) jest stale i znane. Jeśli warunki te są spełnione, a badany proces został wstępnie oceniony jako wydolny [7], to rozregulowanie procesu ze względu na zmienną X może się przejawiać tylko poprzez przemieszczanie się wartości oczekiwanej () na osi liczbowej badanej zmiennej. Problem ten ilustruje rys.4. Przy sporządzaniu tego rysunku przyjęto, ze przedział tolerancji jest ograniczony obustronnie; zob. wzór (6). Załóżmy, że sytuacja pokazana w części A tego rysunku obrazuje proces uregulowany. Mamy mianowicie
- o = = 0 (32)
Oznacza to, że spełniona jest nierówność
p = P(x < xd) + (x > xg) po (33)
W pozostałych częściach rys.4 pokazano sytuacje, w których proces jest rozregulowany. Oznacza to, że
p = P(x < xd) + (x > xd) > po (34)
W części B rys.4 przedstawiono sytuację, gdy nierówność (34) jest spełniona w rezultacie przesunięcia się rozkładu zmiennej X ku niższym wartościom zbioru X . Mamy więc
- xo = < 0 (35)
W części C rys.4 mamy natomiast sytuacje odwrotna:
- xo = > 0 (36)
W celu rozstrzygnięcia w jakim stanie znajduje się obserwowany proces, w kolejnych punktach t = 1,2,... weryfikuje się hipotezy statystyczne dotyczące wartości oczekiwanej () badanej zmiennej diagnostycznej X. Jeśli przedział tolerancji ograniczony jest obustronnie (jak na rys.4), to weryfikacji podlega hipoteza zerowa
Ho: t = xo albo Ho: t - xo = = 0 (37)
wobec hipotezy alternatywnej
H1: t xo albo H1: t - xo = 0 (38)
W przypadku, gdy przedział tolerancji ograniczony jest tylko prawostronnie (zob. wzór (7)), hipoteza zerowa ma postać
Ho: t xo albo Ho: t - xo = 0 (39)
i jest ona weryfikowana wobec hipotezy alternatywnej
H1: t > xo albo H1: t - xo = > 0 (40)
Jeśli natomiast przedział tolerancji ograniczony jest tylko lewostronnie (zob. wzór (8)), to
wówczas
Ho: t ≥ xo albo H1: t - xo = ≥ 0 (41)
oraz
H1: t xo albo H1: t - xo = < 0 (42)
Niezależnie od tego, która spośród wymienionych powyżej hipotez zerowych podlega weryfikacji, obserwowaną charakterystyką z próby jest średnia arytmetyczna
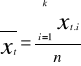
(43)
Diagram przeglądowy ma postać przedstawiona na rys.3. Należy tylko dokonać odpowiedniej zmiany symboli: ![]()
, ![]()
, ![]()
i ![]()
. Dokonując dodatkowo podstawienia
![]()
(44)
możemy określić położenie linii kontrolnych na podstawie podanych powyżej wzorów. Wykorzystując - na przykład - równania (18) i (19) oraz (21) i (22) otrzymujemy:
![]()
(45)
![]()
(46)
![]()
(47)
![]()
(48)
Przedstawione powyżej rozważania zilustrujemy przykładem numerycznym.
Przykład 1
Załóżmy, ze przedział tolerancji zmiennej diagnostycznej X ma postać
X = [13.0; 14.0] (i)
a wartość nominalna xo = 13.5. Załóżmy również, że zmienna diagnostyczna X jest zmienną losową o normalnym rozkładzie prawdopodobieństwa o stałym i znanym odchyleniu standardowym σ = 0.20. Przyjmijmy, że istnieje możliwość oddziaływania na wartość oczekiwaną zmiennej X i ustalenia jej na dowolnym poziomie Xo. W celu zminimalizowania wadliwości (p) należy przyjąć = xo = 13.5. Mamy więc X~N(13.5; 0.20).W odniesieniu do największej dopuszczalnej wadliwości przyjmijmy, że p' = 0.03 (3%).
Na podstawie przyjętych założeń można ocenić wydolność procesu. Mamy mianowicie
p = P(X < 13.0) + P(X > 14.0) =
= [(13.0 - 13.5)/0.20] + [(14.0 - 13.5)/0.20] = (ii)
= (-2.50) + 1 - (2.50) =
= 2 * 0.00621 = 0.01242 (1.242%)
Ponieważ p = 0.01242 < p'o = 0.03, przeto proces jest wystarczająco wydolny, by sprostać wymaganiom odbiorcy produktu. Dla potrzeb sterowania procesem należy przyjąć, że po = 0.01242 (1.242%), albowiem pozwoli to wykorzystać wszystkie możliwości jakimi dysponuje proces. Otwiera to też pewne możliwości negocjacji cenowych w przyszłości, albowiem pozwala oczekiwać wyższej jakości niż ta na, którą zgodził odbiorca. Wadliwość 1.242% uzyskuje się wówczas gdy t = xo = 13.5. W każdym kroku postępowania kontrolnego należy więc weryfikować hipotezę zerową:
Ho: t = 13.5 (iii)
wobec hipotezy alternatywnej
H1: t 13.5 (iv)
Prawdopodobieństwo zbędnej regulacji () ustalimy na poziomie0.01. Ponieważ rozregulowanie procesu może się rozregulować, albo przez przesunięcie t ku wartościom niższym od 13.5 albo ku wartościom wyższym od 13.5, przeto mamy do czynienia z dwustronnym schematem kontrolnym. Przy wyznaczaniu równań linii kontrolnych należy więc wziąć pod uwagę wartość u/2 = u0.005 . Wartość tego kwantyla zmiennej losowej U odczytujemy z następującego zestawienia:
|
0.005 |
0.010 |
0.025 |
0.050 |
0.100 |
u |
2.576 |
2.326 |
1.960 |
1.645 |
1.282 |
zaczerpniętego z [6].
Przyjmijmy, że w każdym kroku postępowania kontrolnego pobierana jest do badania pięcioelementowa próbka (n = 5). Równania linii kontrolnych przedstawiają się następująco:
![]()
![]()
Wyniki badania kolejnych próbek przedstawiono w tablicy 1. Jak łatwo zauważyć w rezultacie badania próbki o numerze t = 5 uzyskano średnią arytmetyczną przekraczającą górną granicę regulacji. Mamy mianowicie ![]()
. Podjęte czynności regulacyjne nie przyniosły spodziewanego rezultatu i w kolejnej próbce (t = 6) uzyskano ![]()
. Podjęte działania usunęły przyczynę rozregulowania. Na uwagę zasługuje to, że w próbkach, które doprowadziły do emisji sygnałów o rozregulowaniu procesu wszystkie wartości xt,i mieściły się w przedziale tolerancji. Zdolność do reagowania na małe zmiany w obserwowanym procesie jest bardzo cenną właściwością karty kontrolnej ![]()
i innych kart stosowanych w przypadku liczbowej oceny właściwości. Liczbowa ocena właściwości pozwala na znacznie lepsze wykorzystanie informacji o produkcie i procesie, zawartych w rezultatach badania próbki, niż alternatywna ocena właściwości.
Odrzućmy obecnie założenie, że odchylenie standardowe (σ) obserwowanej zmiennej diagnostycznej X jest znane i stałe. Przyjmiemy więc teraz, że obydwa parametry rozkładu normalnego (,σ) są znane i nie można założyć, ze którykolwiek z nich jest stały w czasie. W takiej sytuacji naruszenie zadanej normy jakości wykonania (po) może się dokonać nie tylko za sprawą przesuwania się rozkładu wzdłuż osi badanej zmiennej, ale także na skutek zmiany kształtu tego rozkładu. Problem ten ilustruje rys. 5. Na rysunku tym pokazano skutki wzrostu odchylenia standardowego (σ) ponad pewną maksymalną wartość σ0 , przy której (jeśli = xo ) spełniona jest jeszcze nierówność p po . W rozważanej sytuacji niezbędna jest kontrola odchylenia standardowego σ. W każdym kroku postępowania kontrolnego, niezależnie od weryfikacji hipotez dotyczących parametru , poddaje się weryfikacji hipotezę zerową
Ho: σt σo (49)
wobec hipotezy alternatywnej
H1: σt > σo (50)
Do weryfikacji hipotezy (49) wykorzystuje się albo odchylenie standardowe z próbki
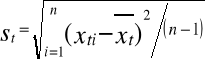
(51)
albo rozstęp z próbki
rt = rt.max - rt.min (52)
Jeśli w każdym kroku postępowania kontrolnego badaniu podlega średnia arytmetyczna z próbki (![]()
) i odchylenie standardowe z próbki (σt ), to mamy do czynienia z kartą kontrolną ![]()
. Jeśli st zastąpimy rozstępem z próbki, to otrzymamy kartę kontrolna ![]()
. Są to karty dwutorowe.
Ustalmy uwagę na karcie kontrolnej ![]()
. Tor ![]()
funkcjonuje tak samo jak karta kontrolna ![]()
. Jedyna różnica polega na tym, że we wzorach (45) - (48) w miejsce σ podstawia się σo . Drugi tor kontrolny służy do weryfikacji hipotezy zerowej (49), wobec hipotezy alternatywnej (50). Linię centralną wykreśla się na poziomie σo , natomiast równanie linii kontrolnej zależy od liczności próbki. Jeśli w każdym kroku postępowania kontrolnego badana jest bardzo liczna próbka
(n ≥ 30), to mamy:
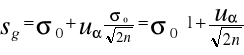
(53)
W praktyce dominują próbki o liczności n < 30. W takiej sytuacji położenie linii kontrolnej wyznacza się według wzoru
![]()
(54)
gdzie ![]()
jest taką wartością zmiennej losowej chi-kwadrat o (n-1) stopniach swobody, że
![]()
(55)
Jeśli na torze s wykreślimy dodatkowo dolna linie kontrolna, to uzyskamy możliwość wykrywania korzystnych zmian w procesie. Jest bowiem niemal reguła, że o ile wzrost zmienności (zróżnicowania) jednostek produktu oznacza pogorszenie jego jakości, o tyle mniejsza zmienność jest niemal zawsze przejawem wyższej jakości.
W zależności od liczności próbek (n) pobieranych do badania linię tę wykreśla się według jednego z następujących wzorów:
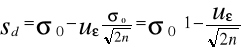
(56)
![]()
(57)
przy czym ![]()
wyznacza się w taki sposób, by
![]()
(58)
Wzór (56) jest szczegółowa postacią ogólnego równania (24). Można go stosować tylko wówczas, gdy n ≥ 30, podobnie jak wzór (53). W przypadku gdy n < 30, stosuje się wzór (57). Zauważmy, że jeśli przedział tolerancji jest ograniczony obustronnie (zob. wzór (6)) i gdy - w konsekwencji - stosuje się dwustronny schemat kontrolny, to śledzenie sygnałów na torze s jest podstawową metodą wykrywania korzystnych zmian w procesie. Dodajmy też, że sygnałom postaci st < sd na torze kontrolnym s powinno towarzyszyć odpowiednie "zagęszczenie" punktów ![]()
wokół linii centralnej xo , na torze ![]()
.
Karta kontrolna ![]()
funkcjonuje tak samo jak karta ![]()
. Różnica polega jedynie na tym, że w przypadku karty kontrolnej ![]()
do weryfikacji hipotezy zerowej (49) wykorzystuje się rozstęp z próbki rn.t , a nie odchylenie standardowe z próbki st . Przy wyznaczaniu położenia linii centralnej i linii kontrolnych na płaszczyźnie diagramu przeglądowego wykorzystuje się zależności zachodzące miedzy odchyleniem standardowym zmiennej diagnostycznej X~N(,σ), a rozstępem (R). Rozstęp (R) jest zmienną losową o realizacjach (r) uzyskiwanych według wzoru (52). Zachodzą następujące związki
![]()
(59)
![]()
(60)
w których E(Rn ) oznacza wartość oczekiwaną zmiennej losowej Rn , natomiast D(Rn ) jest odchyleniem standardowym tej zmiennej. Wartości współczynników dn i fn są stablicowane [6]. Jeśli liczność próbki (n) jest ustalona, to linię centralną na torze r wykreśla się na poziomie
![]()
(61)
Zauważmy, że w odróżnieniu od dotychczas omawianych kart położenie linii centralnej zależy tu od liczności próbki (n). Położenie górnej linii kontrolnej wynika ze wzoru
![]()
(62)
Dolna linia kontrolna może tu być wykorzystana analogicznie jak w przypadku karty kontrolnej ![]()
Równanie tej linii przedstawia się następująco:
![]()
(63)
Jest to szczegółowa postać ogólnego wzoru (24).
W przypadku kart kontrolnych ![]()
oraz ![]()
sygnał o rozregulowaniu obserwowanego procesu emitowany jest wówczas, gdy pojawi się taki sygnał chociażby na jednym torze kontrolnym. Pewne problemy mogą się pojawić wówczas, gdy na torze kontrolnym s, albo r, wystąpi sygnał o korzystnych zmianach w procesie produkcyjnym, a jednocześnie na torze kontrolnym ![]()
nastąpi przekroczenie granic regulacji. Taka konfiguracja sygnałów nie musi oznaczać rozregulowania procesu w sensie nierówności (13). Szersze omówienie tego problemu zainteresowany Czytelnik znajdzie w [6]. Karta ![]()
jest najczęściej stosowana procedura kontrolna typu Shewharta, zwłaszcza w przemyśle amerykańskim. Popularność tej karty ma swoje uzasadnienie historyczne. W latach dwudziestych, kiedy to W.A. Shewhart wprowadzał do praktyki przemysłowej pierwsze karty kontrolne, a także przez wiele następnych lat, czas potrzebny do obliczenia wartości st według wzoru (51) był nieporównanie dłuższy niż czas niezbędny do wyznaczenia wartości rn.t według wzoru (52). Wynikało to z ubóstwa podręcznych środków obliczeniowych w owych latach. Bezpośrednim skutkiem takiego stanu rzeczy była praktyczna przewaga karty kontrolnej ![]()
nad karta ![]()
. Obecnie, w epoce mikrokomputerów i programowanych kalkulatorów elektronicznych, sytuacja zmieniła się całkowicie. Czas niezbędny do obliczenia wartości każdej z tych charakterystyk jest znikomy, a cały proces praktycznie zajmuje tyle czasu, ile trwa wprowadzanie danych liczbowych do urządzenia wykonującego obliczenia. A ponieważ w obu przypadkach należy wprowadzić do owego urządzenia wszystkie wyniki badań, albowiem równolegle biegnie obliczanie średniej arytmetycznej, przeto obliczenie wartości każdej z tych charakterystyk wymaga tyle samo czasu. Siła tradycji jest jednak przemożna i karta kontrolna ![]()
jest nadal znacznie częściej stosowana niż karta ![]()
. Dzieje się tak mimo faktu, ze odchylenie standardowe z próbki jest znacznie lepszym estymatorem odchylenia standardowego (σ) badanej zmiennej diagnostycznej X, niż rozstęp z próbki.
6. Przykłady kart kontrolnych typu Shewharta stosowanych przy alternatywnej ocenie właściwości
Jeśli właściwości każdej jednostki produktu oceniane są alternatywnie, to odpowiednie zmienne diagnostyczne (X) definiuje się jako zerojedynkowe zmienne losowe postaci (4). Jedynym parametrem rozkładu takiej zmiennej losowej jest wadliwość (p) zdefiniowana wzorem (5). W rozważanej sytuacji w każdym kroku postępowania kontrolnego weryfikacji poddaje się hipotezę zerowa
Ho: pt po (64)
wobec hipotezy alternatywnej
H1: pt > po (65)
Tak wiec, poddajemy tu bezpośredniej weryfikacji tę hipotezę, która w przypadku liczbowej oceny właściwości sprawdzana jest pośrednio, poprzez hipotezy zerowe postaci (37), (39), (41) i (49). Rodzi się więc naturalne pytanie o celowość liczbowej oceny właściwości. Odpowiedź na to pytanie jest następująca. W przypadku liczbowej oceny właściwości tryb weryfikacji hipotezy (64) jest wprawdzie pośredni, ale niezbędna liczność próbki jest mniejsza niż w przypadku oceny alternatywnej. Ocena alternatywna jest pomiarem na bardzo słabej skali porządkowej, podczas gdy liczbowa ocena właściwości wiąże się z pomiarem na skali przedziałowej lub nawet ilorazowej. Oznacza to, że w przypadku liczbowej oceny właściwości każdy pomiar dostarcza znacznie więcej informacji o produkcie, niż ocena alternatywna. Z drugiej strony należy jednak pamiętać, że pomiar na mocnej skali wymaga zawsze odpowiedniej aparatury, a jego koszt jest nieporównanie większy niż ocena alternatywna. Dla potrzeb sterowania procesem przy alternatywnej ocenie właściwości definiuje się następujące zmienne losowe:
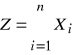
(66)
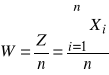
(67)
gdzie Xi oznacza kolejne (i = 1,2,...,n) zerojedynkowe zmienne losowe o jednakowych rozkładach prawdopodobieństwa. Obydwie zmienne (Z, W) mają dwumianowe rozkłady prawdopodobieństwa o takich samych parametrach p i n, ale o rożnych zbiorach wartości. Zmienna losowa Z może przyjmować wartości ze zbioru
Zo = {0, 1, 2,...,n} (68)
natomiast zbiór wartości zmiennej losowej W przedstawia się następująco
W = {0/n = 0, 1/n, 2/n,...,n/n = 1} (69)
Zmienna losowa Z stanowi formalną podstawę karty kontrolnej z. Obserwowana charakterystyka z próby dana jest wzorem
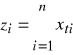
(70)
Jest to liczba elementów niezgodnych (wadliwych) w próbce o liczności n, pobranej do badania w chwili t. Diagram przeglądowy ma postać pokazana na rys. 3. W celu przystosowania tego diagramu do potrzeb karty kontrolnej z należy wyeliminować dolną granicę regulacji, a następnie dokonać następujących podstawień: t = zt , 0 = z0 , g = zg .Linię centralną wykreśla się na poziomie
Z0 = np0 (71)
Jest to największa normalnego.
Mamy mianowicie
![]()
(72)
Dolna linia kontrolna może tu służyć, analogicznie jak w przypadku kart kontrolnych omówionych w punkcie 5, do wykrywania korzystnych zmian w procesie. Położenie tej linii wyznacza się następująco:
![]()
(73)
Kartę kontrolna z można łatwo przekształcić w kartę kontrolną w.
Obserwowana charakterystyka z próby przedstawia się następująco:
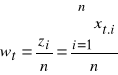
(74)
Jest to frakcja elementów niezgodnych (wadliwych) w próbce o liczności n, pobranej do badania w chwili t. Wartości wt uzyskiwane według podanego wzoru są realizacjami zmiennej losowej W, zdefiniowanej wzorem (67). W celu przystosowania diagramu przeglądowego z rys. 3 do potrzeb karty kontrolnej w należy wyeliminować dolną granicę regulacji (analogicznie jak w przypadku karty kontrolnej z), a następnie dokonać następujących podstawień: t = wt , 0 = w0, g = wg . Położenie linii centralnej określa wzór
![]()
(75)
Równanie górnej linii kontrolnej ma postać
![]()
(76)
Położenie dolnej linii kontrolnej (nie będącej granica regulacji) wyznacza równanie
![]()
(77)
Równania (72) i (73) oraz (76) i (77) są wzorami przybliżonymi. Uzyskiwane przybliżenie jest oczywiście tym lepsze, im większa jest liczność próbki (n). Przy wyznaczaniu położenia tych linii kontrolnych można również posłużyć się dokładnym rozkładem zmiennych losowych Z i W, czyli rozkładem dwumianowym. Problem ten omówiono w [6].
W angielskojęzycznej literaturze przedmiotu karta kontrolna z oznaczana jest symbolem np (ang. np chart), natomiast w odniesieniu do karty kontrolnej w stosowany jest symbol p (ang. p chart). Zauważmy, że zastosowano tu inny sposób oznaczania, niż w przypadku poprzednio omawianych kart kontrolnych. W przypadku kart kontrolnych ![]()
, ![]()
oraz ![]()
zastosowane symbole pochodzą od obserwowanych charakterystyk z próby, natomiast np i p, to symbole wartości oczekiwanych zmiennych losowych, definiowanych dla potrzeb sterowania procesem. Symbolika przyjęta w polskiej literaturze jest bardziej konsekwentna. Karta kontrolna jest zawsze oznaczana symbolem odpowiedniej charakterystyki z próby.
7. Przykłady kart typu Shewharta do kontroli przeciętnej liczby wad (niezgodności) w jednostce
produktu
Wszystkie przedstawione powyżej karty kontrolne mogą być stosowane wówczas, gdy miarą jakości wykonania jest wadliwość zdefiniowana wzorem (1), albo frakcja (procent) jednostek niezgodnych (wadliwych). Ustalmy obecnie uwagę na drugim spośród wyróżnionych przypadków, gdy jakość procesu albo strumienia produktu oceniana jest na podstawie przeciętnej liczby niezgodności (wad). Charakterystykę tę oznaczyliśmy powyżej symbolem , a nierówności (14) i (15) opisują stan uregulowania i rozregulowania procesu. Liczba niezgodności (wad) w jednostce produktu jest zmienną losową (Y) o przeliczalnym zbiorze wartości
Yo = {0, 1, 2,...} (78)
Przyjmuje się zwykle, że na zbiorze tym rozpięty jest rozkład Poissona [12], którego szczegółowa postać określana jest przez parametr . Przy rozwiązywaniu praktycznych problemów wartość tego parametru, czyli przeciętnej liczby wad (niezgodności), musi być odniesiona do ustalonej jednostki produktu. Może to być jednostka elementarna lub agregatowa, przy czym każda z nich może być jednostką rzeczywistą lub umowną. Jeśli - na przykład - podejmujemy działania mające na celu monitorowanie jakości usług hotelowych, to jako jednostkę produktu przyjmuje się najczęściej dobę hotelowa. Jest to umowna jednostka elementarna . W procesie produkcji ołówków, rzeczywistą jednostką elementarną jest pojedynczy ołówek, natomiast często stosowaną umowną jednostką agregatową jest tuzin. Ustalmy uwagę na ogólnym przypadku, gdy w każdym kroku postępowania kontrolnego (t = 1, 2,...) badaniu podlega umowna, agregatowa jednostka produktu składająca się z n jednostek elementarnych. W takiej sytuacji do sterowania procesem można wykorzystać kartę kontrolna c. Obserwowana charakterystyka z próby ma postać
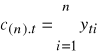
(79)
gdzie yti jest liczbą niezgodności (wad) w i-tej elementarnej jednostce produktu, należącej do n-elementowego zbioru o numerze t. Charakterystyki c(n).t wykorzystywane są do weryfikacji hipotez zerowych postaci
Ho: (n).t (n).0 (80)
wobec hipotez alternatywnych
H1: (n).t > (n).0 (81)
gdzie (n)0 oznacza największą dopuszczalną przeciętną liczbę niezgodności (wad) w agregatowej jednostce produktu składającej się z n jednostek elementarnych. Mamy więc znowu do czynienia z jednostronnym (prawostronnym) schematem kontrolnym. W konsekwencji, na diagramie przeglądowym (zob. rys.3) wykreślamy tylko linię centralną (na poziomie (n).0 ) oraz górną linię kontrolną (c(n).g), tylko ta linia jest bowiem granicą regulacji. Dolna linia kontrolna służyć może, analogicznie jak w kartach omówionych powyżej, do wykrywania korzystnych zmian w kontrolowanym procesie, będących przejawem postępu technologicznego (biernego lub wymuszonego). Przy wyznaczaniu linii kontrolnych wykorzystywany jest fakt, że rozkład Poissona można aproksymować za pomocą rozkładu normalnego o parametrach: , ![]()
.
Mamy wiec
![]()
(82)
![]()
(83)
Bardzo często liczbę niezgodności (wad) odnosi się do elementarnej (umownej lub rzeczywistej) jednostki produktu. W takiej sytuacji hipoteza zerowa weryfikowana w każdym kroku postępowania kontrolnego przybiera postać
H0: (1).t (1).0 (84)
natomiast hipoteza alternatywna przedstawia się następująco
H1: (1).t > (1).0 (85)
przy czym
(1).0 (n).0/n (86)
(1).t (n).t/ n (87)
W tak zmienionym układzie wnioskowania do sterowania procesem wykorzystuje się kartę kontrolną u. Obserwowana charakterystyka z próby ma postać
ut = c(n).t/n (88)
Wzory pozwalające wyznaczać położenie linii kontrolnych na diagramie przeglądowym otrzymujemy dzieląc obydwie strony równań (82) i (83) przez n. Postępując w ten sposób otrzymujemy:
![]()
(89)
![]()
(90)
Karta u jest szczególnie użytecznym narzędziem sterowania procesem wówczas, gdy nie można zapewnić stałej liczności próbek produktu, które podlegają badaniu polegającemu na zliczaniu niezgodności lub wad. W takiej sytuacji charakterystyka z próby (88) przybiera postać
![]()
(91)
gdzie
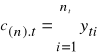
(92)
Emisja sygnału o rozregulowaniu procesu następuje wówczas, gdy punkt (t, ut) znajdzie się poza górną granicą regulacji, której położenie określone jest przez równanie
![]()
(93)
Z równania tego wynika bezpośrednio, że położenie granicy regulacji zmienia się w zależności od liczności badanej próbki. Jeśli n rośnie, to ug.t przybliża się do lii centralnej (1).0 , i odwrotnie, jeśli n maleje, to ug.t oddala się od lii centralnej (1).0 , zachowując równoległość względem niej. Tak samo reaguje na zmiany liczności próbki dolna linia kontrolna, nie będąca granicą regulacji. Równanie tej linii przedstawia się następująco:
![]()
(94)
Zmienność położenia linii kontrolnych utrudnia korzystanie z karty kontrolnej u jako algorytmu graficznego. Znacznie wygodniejszy jest algorytm numeryczny, którego funkcjonowanie zilustrujemy przykładem.
Przykład 2
Jakość produktu oceniano na podstawie przeciętnej liczby niezgodności. Największa przeciętna liczbę niezgodności w elementarnej jednostce produktu ustalono na poziomie (1).0 = 1.00. Zastosowana technika pobierania próby nie pozwalała na utrzymanie jej liczności na stałym poziomie. Do sterowania procesem postanowiono zastosować kartę kontrolna u. Przy wyznaczaniu równania granicy regulacji (górnej linii kontrolnej) przyjęto = 0.01. Mamy wiec u0.01 = 2.326 i w konsekwencji, na podstawie równania (93), otrzymujemy
![]()
(i)
Przy wyznaczaniu dolnej linii kontrolnej, służącej do wykrywania korzystnych zmian w procesie, przyjęto = 0.05. Mamy wiec u0.05 = 1.645. Wykorzystując równanie (94) otrzymujemy
![]()
(ii)
Wyniki badań i ich analizę przedstawiono w tablicy 2. W kolumnach 1, 2 i 3 tej tablicy podano rezultaty badania kolejnych dziesięciu próbek. W kolumnie 4 zestawiono wartości ut obliczone według wzoru (91). W kolumnach (5) i (6) podano natomiast wartości ug.t i ud.t , wyznaczone według wzorów (i), (ii). W punkcie t = 6 pojawił się sygnał o rozregulowaniu procesu. Uzyskana wartość u6 = 2.21 > ug.6 = 1.62 nakazywała odrzucić hipotezę zerowa Ho:(1).0 1.00, na korzyść hipotezy alternatywnej H1: (1).0 > 1.00. Nie pojawiły się sygnały korzystnych zmianach w procesie.
Dodajmy, że jeśli nie ma możliwości utrzymania liczności kolejnych próbek na stałym poziomie, to stosowanie wszystkich omówionych powyżej kart kontrolnych staje się kłopotliwe. W takich sytuacjach najlepszym rozwiązaniem wydaje się zrezygnowanie z karty kontrolnej jako algorytmu graficznego i potraktowanie jej jako procedury numerycznej.
Literatura cytowana
[1] G.A.Barnard; Sampling inspection and statistical decisions, Journal of the Royal Statistical
Society, nr B 16, 1954
[2] G.A.Barnard; New methods of quality control, Journal of the Royal Statistical Society, nr A
126, 1963
[3] J.B.Czermiński, A.Iwasiewicz, Z.Paszek, A.Sikorski; Metody statystyczne dla chemików,
Wydawnictwo Naukowe PWN, Warszawa, 1992
[4] W.D.Evan; When and how to use cu-sum charts, Technometrics, nr 5, 1963
[5] H.Gitlow, S.Gitlow, A.Oppenheim, R.Oppenheim; Tools and methods for the improvement
of quality; Irwin, Homewood (IL), Boston (MA), 1989
[6] A.Iwasiewicz; Statystyczna kontrola jakości w toku produkcji; systemy i procedury, PWN,
Warszawa, 1985
[7] A.Iwasiewicz; Statystyczna analiza wydolności procesu, Normalizacja, nr 8, 1996
[8] J.M.Juran; Handbook of quality, McGraw Hill, New York, 1962
[9] K.W.Kemp; The average run lenght of the cumulative sum chart when a V - mask is used,
Journal of the Royal Statistical Society, nr B 23,1961
[10] D.C.Montgomery; Introduction to statistical quality control, wyd. II, J.Wiley & Sons, New
York, 1991
[11] J.Obalski; Statystyczna kontrola jakości podczas produkcji, PWT, Warszawa, 1955
[12] J.Oderfeld; Zarys statystycznej kontroli jakości, PWN, Warszawa, 1954
[13] E.S.Page; Continuos inspection shemes, Biometrika, nr 41, 1954
[14] W.A.Shewhart; Quality control charts, Bell System Technical Journal, nr 5, 1926
[15] Slownik jakosci, WNT, Warszawa, 1980
Normy
[16] ISO 8258: 1991 "Shewhart control charts"
[17] PN-ISO 3534-2; 1993 Statystyka - Terminologia i symbole. Część 2 Statystyczna kontrola
jakości
1
Wyszukiwarka
Podobne podstrony:
art folia 00 05, Andrzej Iwasiewicz
SYL 5, referat prof. A. Iwasiewicza
SEM2 SYL
Scenariusz zabaw andrzejkowej dla przedszkolaków, pomoce do pracy z dziećmi
Święty Andrzeju, Przedszkole, Andrzejki
Andrzejki, PRZEDSZKOLE, Andrzejki Scenariusze,Wróżby
Andrzejki z rodzicami scenariusz
Andrzejk1, scenariusze zajęć
sprawko andrzeja, gik, semestr 3, fizyka, wysypisko
New Age, 01 ANDRZEJ WRONKA - TRÓJCA ŚWIĘTA - META JĘZYK, P. Andrzej Wronka
Wróżby andrzejkowe, Przedszkole, Dla dzieci, Andrzejki
Andrze
Andrzejkowe wróżby
praca licencjacka finansowanie msp za pomocą funduszy venture capital m andrzejewicz
SCENARIUSZ SZKOLNEJ IMPREZY ANDRZEJKOWEJ, karty tymka, UROCZYSTOŚCI Z OKAZJI (Andrzejki)
andrzejkigazetka(1)(1), Gazetka szkolna
ANDRZEJKI 1, PROWADZENIE ZAJĘĆ, ANDRZEJKI
PODZIAŁ I KLASYFIKACJA FIR II, Lotnictwo, ppl, Andrzej Niemojewski PPL, od szefowej, Prezentacje i o
więcej podobnych podstron