LABORATORIUM PODSTAW MIERNICTWA
ĆWICZENIE NR 2
POMIARY OSCYLOSKOPOWE
Patryk Wołowicz EiT sem 2
WZORCOWANIE KANAŁÓW X i Y OSCYLOSKOPU NAPIĘCIEM STAŁYM.
Wzorcowanie kanałów oscyloskopu odbywa się metodą najmniejszych kwadratów.
Kanał Y był wzorcowany dla stałej napięciowej DY=1V/cm. Wyniki pomiarów zawiera poniższa tabela:
y |
[cm] |
1 |
2 |
3 |
4 |
-4 |
-3 |
-2 |
-1 |
Uy |
[ V ] |
1,29 |
2,41 |
3,54 |
4,64 |
-4,64 |
-3,52 |
-2,42 |
-1,3 |
Dypom |
[V/cm] |
1,29 |
1,205 |
1,18 |
1,16 |
1,16 |
1,733 |
1,21 |
1,3 |
σy |
[ % ] |
9,709 |
2,480 |
0,354 |
-1,346 |
-1,346 |
-0,212 |
2,905 |
10,559 |
Dyobl |
[V/cm] |
1,175833 |
|||||||
przy czym:
Dypom=Uy/y; Dyobl - współczynnik kierunkowy prostej Uy =myy+ny, wyznaczony metodą najmniejszych kwadratów;
σy=(Dypom - Dyobl)/Dyobl
Poniżej znajduje się wykres zależności σy(y):
Kanał X wzorcowałem dla stałej napięciowej DX=1V/cm w podobny sposób jak kanał Y. Oto wyniki i wykres funkcji σx(x):
x |
[cm] |
1 |
2 |
3 |
4 |
-4 |
-3 |
-2 |
-1 |
Ux |
[ V ] |
1,33 |
2,58 |
3,83 |
5,04 |
-5,12 |
-3,86 |
-2,65 |
-1,41 |
Dxpom |
[V/cm] |
1,33 |
1,29 |
1,276 |
1,26 |
1,28 |
1,286 |
1,325 |
1,41 |
σx |
[ % ] |
3,757 |
0,637 |
-0,403 |
-1,703 |
-0,143 |
0,377 |
3,367 |
9,998 |
Dxobl |
[V/cm] |
1,281833 |
|||||||
POMIAR WSPÓŁCZYNNIKA WYPEŁNIENIA PRZEBIEGU PROSTOKATNEGO.
Współczynnik wypełnienia przebiegu wyraża się wzorem:
gdzie ti - czas trwania impulsu, a T - okres impulsu.
Pomiary przeprowadzamy najpierw dla przebiegu o okresie 600μs i czasie trwania impulsów 120μs . Drugim był przebieg o okresie 600μs, i czasie trwania 480μs . Okres impulsu, czas jego trwania, oraz obliczone na podstawie powyższego wzoru współczynniki wypełnienia dla obydwu przebiegów, zostały pokazane w tabeli zamieszczonej na następnej stronie:
T [μs] |
600 |
ti1 [μs] |
120 |
ti2 [μs] |
480 |
k1 |
0,200 |
k2 |
0,800 |
POMIARY NAPIECIA I CZASU OSVYLOSKOPEM.
Ćwiczenie to przeprowadzałem dla układu całkującego pobudzanego przebiegiem prostokątnym o okresie 600 μs i wypełnieniu 1/2.
Na ekranie oscyloskopu otrzymałem następujący wykres napięcia:
Wykres otrzymałem dla stałej napięciowej 1V/cm oraz 0,1ms/cm, czyli U1=3,0cm * 1V/cm=3,0 V , natomiast t1= (4,5-2,2)cm*0,1 ms/cm=0,23 ms . Napięcie U2= 1,2 cm* 1V/cm=1,2 V.
Na tej podstawie mogę wyznaczyć stałą czasową RC układu:
czyli RC=0,251012 s=251 ms.
Tymczasem wynik teoretyczny dla elementów R=1 kΩ i C=240 nF wynosi RC=240 ms.
Na podstawie powyższych obliczeń widać, że wyniki różnią się między sobą bardzo nieznacznie.
RÓZNICOWE POMIARY NAPIĘĆ POMIĘDZY DWOMA PUNKTAMI NIEUZIEMNIONYMI.
Do tego punktu wykorzystałem oscyloskopu w trybie pracy sumacyjnej podłączając sygnały napięć do dwóch kanałów i uziemiając przewody „zimne”.
Otrzymałem następujący wykres:
Na podstawie przebiegu mogę także tym razem wyznaczyć stałą czasową RC. Biorąc pod uwagę parametry : 1V/cm i 0,1ms/cm otrzymałem wynik RC=0,238322 s= 238 ms.
Tym razem różnica jest jeszcze mniejsza, właściwie pomijalnie mała.
OBSERWACJA PRZEBIEGÓW W UKŁADACH CYFROWYCH.
Obserwowałem przebiegi na liczniku binarnym. Kanał B podłączyłem do wejścia licznika, natomiast kanał A kolejno do wyjść A,B,C,D i zanotowałem ile okresów sygnału wejściowego przypada na jeden okres przebiegu wyjściowego:
TA = 2 Tin TB = 4 Tin
TC = 8 Tin TD = 16 Tin.
W drugiej części kanał A podłączyłem do wyjścia bramki OUT natomiast kanał B kolejno z wejściami IN1 oraz IN2, obserwując przebiegi binarne.
Rysunki tych przebiegów zamieszczam poniżej:
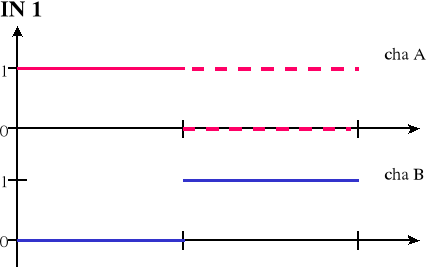
Jak widać z rysunku bramka IN1 jest otwarta dla stanu logicznego 1.
Dla bramki IN2 zaobserwowałem następujące przebiegi:
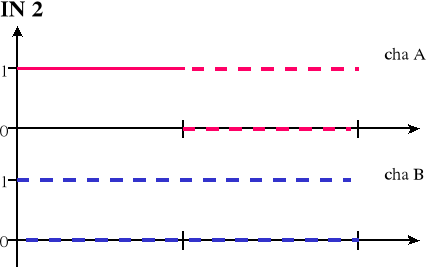
POMIARY PARAMETRÓW IMPULSÓW.
Celem tego ćwiczenia było wyznaczenie :
czasu narastania tr
czasu opadania tf
czasu trwania tw
okresu T.
Dla impulsu o następującym kształcie:
Wyniki zawarłem w tabeli:
tr [μs] |
80 |
tf [μs] |
80 |
tw [μs] |
200 |
T [μs] |
800 |
OBSERWACJA CHARAKTERYSTYK I=f(U) DIÓD W OBSZARZE PRZEWODZENIA.
Charakterystyki prądowo-napięciowe zbadałem dla trzech diod półprzewodnikowych: krzemowej, germanowej, LED. Wszystkie wykresy wykreśliłem biorąc pod uwagę parametry kanałów oscyloskopu, tzn. 0,5V/cm i 10mA/cm.
Dioda Ge:
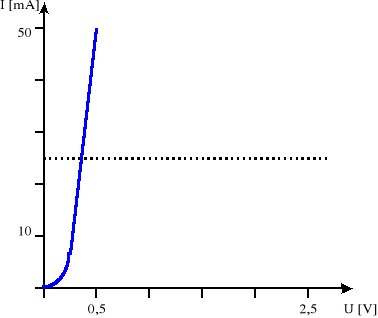
Dioda Si:
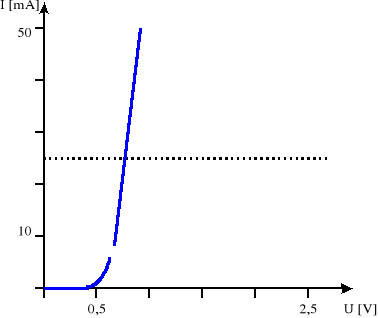
Dioda LED:
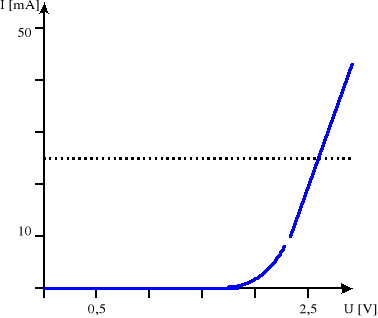
Napięcie przewodzenia badanych diod dla I=25mA można odczytać opierając się na naszych oscylogramach, a stąd ma ono wartość:
- dla diody germanowej: 0,4V
- dla diody krzemowej: 0,75V
- dla diody LED: 2,5V .
Rezystancję dynamiczną badanych diod dla I=25mA uzyskujemy poprzez wyliczenie cotangensa kąta nachylenia stycznej do przebiegu I=f(U). Zależność ta wyraża się wzorem:
Liczba „k” w powyższym wzorze jest współczynnikiem skali zależnym od skali poszczególnych osi. Kąty zastały przeze mnie odczytane z rysunków wykonanych na papierze milimetrowym.
Rodzaj diody |
GERMANOWA |
KRZEMOWA |
LED |
α |
70o |
68o |
78o |
ctgα |
0,364 |
0,404 |
0,213 |
k |
10 |
10 |
50 |
Rd[Ω] |
3,64 |
4,04 |
10,63 |
Rezystancję statyczną badanych diod otrzymujemy korzystając z wzoru:
Powyższy wzór oznacza, iż rezystancja statyczna jest stosunkiem wartości napięcia do wartości prądu w punkcie zadanym „A”. Wartość prądu wynosi 25mA dla wszystkich diod. Zmienia się tylko wartość napięcia, która jest równa obliczonej powyżej wartości napięcia przewodzenia poszczególnych diod. Rezystancję statyczną można też obliczyć graficznie, tzn. jako iloczyn cotangensa kąta nachylenia prostej łączącej punkt „A” z początkiem układu współrzędnych, oraz współczynnika skali. Zależność ta wyraża się więc podobnym wzorem, jak rezystancja dynamiczna.
Zestawienie obliczeń rezystancji statycznej w sposób teoretyczny i graficzny przedstawia poniższa tabela:
Rodzaj diody |
GERMANOWA |
KRZEMOWA |
LED |
Metoda teoretyczna |
|||
U[V] |
0,4 |
0,75 |
2,5 |
Rs[Ω] |
16,0 |
30 |
100 |
Metoda graficzna |
|||
β |
33o |
18o |
27o |
ctgβ |
1,603 |
3,078 |
1,963 |
k |
10 |
10 |
50 |
Rs[Ω] |
16,03 |
30,78 |
98,15 |
INSTYTUT TECHNOLOGII ELEKTRONICZNEJ |
||
ZAKŁAD MIERNICTWA ELEKTRONICZNEGO |
||
LABORATORIUM PODSTAW MIERNICTWA |
||
GRUPA 2 |
||
Temat: |
Imię i nazwisko |
Patryk Wołowicz |
|
Data wykonania ćwiczenia |
12.11.97 |
|
Data odbioru sprawozdania |
|
|
Ocena zaliczenia |
|
|
Uwagi: |
|
|
|
|
tabela 3.1
XT |
cm |
|
DtX |
ms/cm |
|
fX |
Hz |
|
δfX |
% |
|
tabela 3.2
XT |
cm |
|
Xτ |
cm |
|
ϕ |
° |
|
δϕ |
% |
|
tabela 3.3
2Xm |
cm |
|
2X0 |
cm |
|
ϕ |
° |
|
δϕ |
% |
|
tabela 3.4
Tp |
s |
10-3 |
10-2 |
10-1 |
1 |
10 |
100 |
stan licznika |
|
|
|
|
|
|
|
jednostka |
kHz/Hz |
|
|
|
|
|
|
przepełnienie |
tak/nie |
|
|
|
|
|
|
fX |
|
|
|
|
|
|
|
δdyskr. |
% |
|
|
|
|
|
|
tabela 3.5
|
Seria I |
Seria II |
Nr |
fX Hz |
fX Hz |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
czas rej. |
|
|
Tabela 3.6
fg |
fX (M-4650) |
fX (PFL-30) |
δfx |
kHz |
kHz |
kHz |
% |
10 |
|
|
|
20 |
|
|
|
50 |
|
|
|
80 |
|
|
|
100 |
|
|
|
120 |
|
|
|
140 |
|
|
|
160 |
|
|
|
180 |
|
|
|
195 |
|
|
|
Wyszukiwarka
Podobne podstrony:
NO3 POM CZESTOTLI FAZY, MR3 OPR, LABORATORIUM PODSTAW MIERNICTWA
NO3 POM CZESTOTLI FAZY, MAR3, LABORATORIUM PODSTAW MIERNICTWA
NO6 RLC MOSTKI, MR6 OPR, LABORATORIUM PODSTAW MIERNICTWA
2. pomiary oscyloskopowe, protokol cw2, Laboratorium Podstaw Miernictwa
pom nap okr zm 1, Informatyka, Podstawy miernictwa, Laboratorium
pom mocy ukl trojfaz, Informatyka, Podstawy miernictwa, Laboratorium
NO2 POM OSCYLOSKOPOWE, MIERNIC2, POMIARY OSCYLOSKOPOWE
pom nap okr zm a, Informatyka, Podstawy miernictwa, Laboratorium
bledy syst przyp, BS I P, Laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego4
NO1 WZORCOWANIE, thom1b, Laboratorium Podstaw Miernictwa
1. wzorcowanie, protokol cw1, Laboratorium Podstaw Miernictwa
1. wzorcowanie, protokol cw1, Laboratorium Podstaw Miernictwa
3. pomiar częstotliwości fazy, protokol cw3, Laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego4 (1)
Sprawozdanie z laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego6
Laboratorium z podstaw Miernictwa Elektronicznego
więcej podobnych podstron