Rok akademicki 1996/97	Laboratorium z fizyki
Nr ćwiczenia: 65	Badanie rozkładu elektronów w zależności od ich prędkości.
Elektronika telekomunikacja Grupa: E.02	Tomasz Król
Data wykonania	Ocena		Data zaliczenia	Podpis
20.03.1997	T
	S

1.Zasada pomiaru

W doświadczeniu w celu otrzymania rozkładu elektronów w zależności od ich prędkości, bada się rozkład elektronów w lampie elektronowej stosując metodę potencjału hamującego. Na anodę lampy próżniowej z żarzoną katodą podaje się napięcie hamujące, przeszkadzające dochodzeniu elektronów do anody. Dochodzą do niej tylko te elektrony, których energia kinetyczna jest większa od pracy sił pola elektrycznego wywołującego hamowanie. Mierząc prąd anodowy przy różnych napięciach hamowania, można bezpośrednio śledzić rozkład ilości termoelektronów w zależności od ich energii. Rozkład ten jest zgodny z rozkładem Maxwella - Boltzmana:

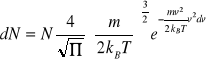
gdzie:

dN - liczba elektronów ze składowymi prędkości zawartymi w przedziale prędkości vv+dv

N - koncentracja swobodnych elektronów, które opuściły metal

m - masa elektronu

kB - stała Boltzmana

T - temperatura bezwzgledna

Zależnośc prądu anodowego od napięcia hamującego:

gdzie : U - napięcie hamujące

Ia0 - natężenie prądu anodowego w przypadku, gdy różnica potencjałów między anodą i katodą wynosi zero

Wykres zależności lnIa lub ln Ia/Ia0 od wartości napięcia anodowego powinien być linią prostą daną równaniem:

lub

Liniowa zależność lnIa lub ln Ia/Ia0 od wartości napięcia hamującego potwierdza założenia o Maxwellowskim rozkładzie prędkości elektronów termoemisji. Znając współczynnik nachylenia prostej:
można obliczyć temperaturę gazu elektronowego w lampie , a tym samym temperaturę katody.

Znając wartość napięcia hamującego U można łatwo określić prędkość elektronów korzystając z zależności:

m - masa elektronu

v - prędkość elektronu

e - ładunek elementarny

2.Schemat układu pomiarowego

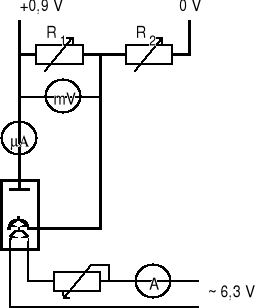
Prąd żarzenia Iż=0,66 A

Ocena dokładności pojedynczych pomiarów

W doświadczeniu stosowano urządzenia:

a) miliwoltomierz: klasa 0,5 zakres 750 mV ΔU=3,75 mV

b) mikroamperomierz: klasa 0,5 zakres 750 A Ra = 60 ΔI=3,75 μA

c) amperomierz: klasa 0,5 zakres 1 A

Iż= klasa*zakres/100= 0,5*1A/100= 0,005 A

4.Tabele pomiarowe

Lp.	Iz [A]	Ia [μA]	U [mV]	IaRa [mV]		U'=U-IaRa [mV]	Ua=U'+Δϕ [mV]	ln Ia		ln Ia/Io
1	0,66	750	550	45,0		505,0	x	6,62		1,27
2	0,66	700	500	42,0		458,0	x	6,55		1,20
3	0,66	650	450	39,0		411,0	x	6,48		1,13
4	0,66	600	400	36,0		364,0	x	6,40		1,05
5	0,66	540	350	32,4		317,6	x	6,29		0,94
6	0,66	490	300	29,4		270,6	x	6,19		0,85
7	0,66	440	250	26,4		223,6	x	6,09		0,74
8	0,66	390	200	23,4		176,6	x	5,97		0,62
9	0,66	350	150	21,0		129,0	x	5,86		0,51
10	0,66	300	100	18,0		82,0	x	5,70		0,36
11	0,66	260	50	15,6		34,4	x	5,56		0,21
12	0,66	210	0		12,6	-12,6	x	5,35	0			Δn/no	EK [meV]	V [m/s]
13	0,66	220	0		13,2	-13,2	-38,6	5,39	0			0,05	39	116
14	0,66	170	-50		10,2	-60,2	-85,6	5,14	-0,26			0,23	86	173
15	0,66	130	-100		7,8	-107,8	-133,2	4,87	-0,53			0,18	133	216
16	0,66	100	-150		6,0	-156,0	-181,4	4,61	-0,79			0,14	181	252
17	0,66	70	-200		4,2	-204,2	-229,6	4,25	-1,15			0,14	230	284
18	0,66	50	-250		3,0	-253,0	-278,4	3,91	-1,48			0,09	278	313
19	0,66	30	-300		1,8	-301,8	-327,2	3,40	-1,99			0,09	327	339
20	0,66	20	-350		1,2	-351,2	-376,6	3,00	-2,40			0,05	377	364
21	0,66	10	-400		0,6	-400,6	-426,0	2,30	-3,09			0,05	426	387
22	0,66	0	-450		0,0	-450,0	-475,4	∞	∞			0,05	475	409

5.Przykładowe obliczenia wyników pomiarów wielkości złożonej

Zakres mikroamperomierza (750 μA) nie pozwolił nam na prowadzenie dalszych obliczeń.

Obliczanie wartości napięcia na mikroamperomierzu

- dla kierunku przewodzenia lp. 7 J_aR_a = 440 · 10^-6 · 60 = 26,4 mV

- dla kierunku zaporowego lp. 18 J_aR_a = 50· 10^-6 · 60 = 3,0 mV

Obliczanie napięcia na diodzie

- dla kierunku przewodzenia lp. 7 U' = U - J_aR_a = 250 - 26,4 = 223,6 mV

- dla kierunku zaporowego lp. 18 U' = U - J_aR_a = -250 - 3,0 = -253,0 mV

Obliczanie kontaktowej różnicy potencjałów Δϕ.

Posłużyłem się równaniami prostych aproksymujących z wykresu ln Ia/Io = f (U'), które w miejscu przecięcia się wyznaczyły nam dokładną wartość x, czyli nasze szukane Δϕ.

y = 0,0024x + 0,152

y = 0,0077x + 0,2865

Δϕ = -25,4mV

Obliczanie rzeczywistego napięcia na diodzie (uwzględniając Δϕ):

- dla kierunku zaporowego lp. 18 U_a = U' + Dj = -253,0 + (-25,4) = - 278,4 mV

Obliczenie temperatury katody.

Do obliczeń potrzeba nam jest wartość tgα, którą obliczymy z wykresu ln Ia/Io = f (U').

Wykorzystujemy równanie prostej aproksymującej dla kierunku zaporowego, która pozwola nam w łatwy sposób obliczyć tgα

y = 0,0077x + 0,2865

Podstawiając za x dowolną wartość, otrzymuję y (uwzględniamy jednostkę)

tgα = y/x *1000 = 10,6

Ze wzoru obliczam temperaturę katody, dla kierunku zaporowego, wynosi ona: 1,6*10-19/(1,3*10-23*10,6)= 1161 K.

Obliczanie względnej liczby atomów.

Wyniki podane w tabeli.

Obliczanie energii kinetycznej lp. 18 E_k = e · U_a = 278,4 meV

Obliczanie prędkości elektronów lp. 18

6.Rachunek błędów

Błąd maksymalny spadku napięcia na miliamperomierzu obliczyłem metodą różniczki logarytmicznej

IaRa= 3 mV*(3,75/250)= 0,045 mV

Ponieważ należy rozważać najgorszy przypadek ,gdy błędy maksymalne się dodają, więc błąd rzeczywistego napięcia na diodzie wynosi:

U' = ΔU + Δ IaRa= 4 mV

7.Uwagi i wnioski

Błędy wynikające z zastosowanych przyrządów podane są w punkcie 6. Trudno jest określić błąd powstały przy wyznaczaniu różnicy potencjałów . Przypuszczalnie jest bardzo mały ponieważ został wyliczony przy pomocy dość dokładnych danych (równania prostych aproksymujących). Na wykresach z powodów technicznych nie zostały naniesione błędy pomiarowe.

Charakterystyka diody, jak i wykres funkcji rozkładu Maxwella-Boltzmana wg. energii zasadniczo pokrywają się z danymi zamieszczonymi w literaturze. Wyniki temperatury katody możemy uważać za poprawne ,zgadzają się z wynikami zamieszczonymi w literaturze.

Doświadczenie to ma charakter statystyczny i cechuje się dużą niedokładnością. Wynika to z tego, że zbadanie E_k i v elektronu jest trudne ze względu na przypadkowy charakter wypływu elektronów z katody. Prędkości te możemy jedynie określić w pewnym przybliżeniu i z dość dużym błędem.

---