Ćwiczenie nr 3 - Prawo Malusa
Opis wykonania ćwiczenia
Do wcześniej przygotowanego układu doświadczalnego dołączyliśmy dwa polaryzatory, które ustawiliśmy w jednej linii z detektorem. Detektor podłączony był do amperomierza, który mierzył natężenie światła przechodzącego przez polaryzator. Następnie ustawiliśmy drugi polaryzator (analizator) tak aby jego oś pokrywała się z kierunkiem polaryzacji. Wtedy to właśnie amperomierz wskazywał maksymalne natężenie prądu.
Wartość tę osiągnęliśmy dla kąta 46, przyjęliśmy ją za nasz kąt początkowy 0. Następnie obracaliśmy analizator co 5 stopni aż do 90 i zapisywaliśmy natężenie prądu wskazywane przez amperomierz przy danym pomiarze.
Tabela z wynikami pomiarów
α [o] |
∆ α [o] |
I [mA] |
Zakres[mA] |
Klasa |
∆ I [mA] |
∆(cos2α) |
cos2α |
0 |
2 |
2,05 |
3 |
2,5 |
0,075 |
0,000 |
1,000 |
5 |
2 |
1,97 |
3 |
2,5 |
0,075 |
0,003 |
0,992 |
10 |
2 |
1,95 |
3 |
2,5 |
0,075 |
0,006 |
0,970 |
15 |
2 |
1,92 |
3 |
2,5 |
0,075 |
0,009 |
0,933 |
20 |
2 |
1,9 |
3 |
2,5 |
0,075 |
0,011 |
0,883 |
25 |
2 |
1,85 |
3 |
2,5 |
0,075 |
0,013 |
0,821 |
30 |
2 |
1,75 |
3 |
2,5 |
0,075 |
0,015 |
0,750 |
35 |
2 |
1,65 |
3 |
2,5 |
0,075 |
0,016 |
0,671 |
40 |
2 |
1,55 |
3 |
2,5 |
0,075 |
0,017 |
0,587 |
45 |
2 |
1,35 |
3 |
2,5 |
0,075 |
0,017 |
0,500 |
50 |
2 |
1,15 |
3 |
2,5 |
0,075 |
0,017 |
0,413 |
55 |
2 |
1,05 |
3 |
2,5 |
0,075 |
0,016 |
0,329 |
60 |
2 |
0,9 |
1 |
2,5 |
0,025 |
0,015 |
0,250 |
65 |
2 |
0,72 |
1 |
2,5 |
0,025 |
0,013 |
0,179 |
70 |
2 |
0,54 |
1 |
2,5 |
0,025 |
0,011 |
0,117 |
75 |
2 |
0,36 |
1 |
2,5 |
0,025 |
0,009 |
0,067 |
80 |
2 |
0,23 |
0,3 |
2,5 |
0,0075 |
0,006 |
0,030 |
85 |
2 |
0,1 |
0,3 |
2,5 |
0,0075 |
0,003 |
0,008 |
90 |
2 |
0,05 |
0,1 |
2,5 |
0,0025 |
0,000 |
0,000 |
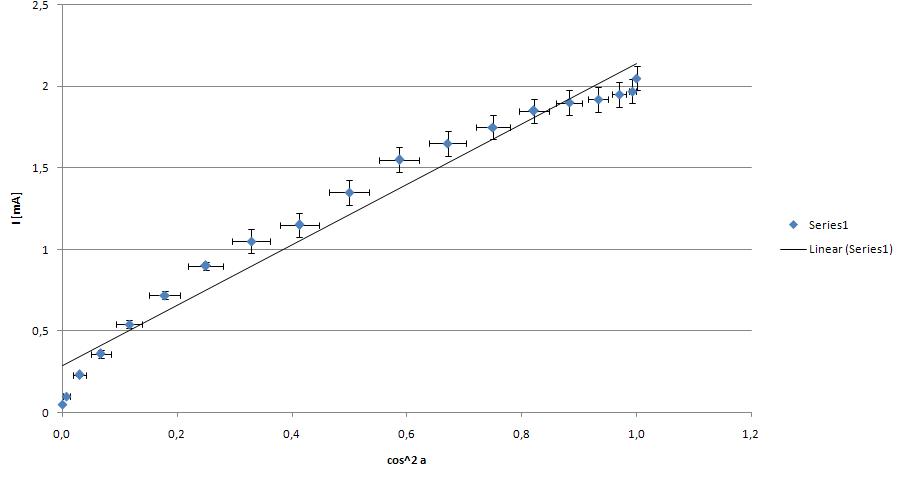
Wynik przeprowadzonego ćwiczenia przedstawiamy na poniższym wykresie. Na osi OY odkładamy kolejne wartości I a na osi OX odpowiadające im wartości cos2 α. Ponieważ jest to zależność liniowa to korzystając z metody najmniejszych kwadratów wyliczamy współczynnik kierunkowy osi który odpowiada wartości I0. Błąd maksymalny cos2 α wyraża się wzorem:
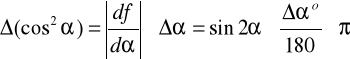
Z metody najmniejszych kątów dowiadujemy się, że I0 wynosi :
I0=(1,85±0,17)mA
