Wydział: Inżynierii Środowiska
|
Dzień/godzina Poniedziałek / 11:15 - 14:00
|
Nr zespołu: 6 |
|||
|
Data: 2.04.2012 |
|
|||
Nazwisko i Imię |
Ocena z przygotowania: |
Ocena ze sprawozdania: |
Ocena: |
||
Wyszyńska Joanna Lebida Rafał Biruk Jarosław |
|
|
|
||
Prowadzący:
|
Podpis prowadzącego: |
||||
Badanie osłabienia promieniowania gamma przy przechodzeniu przez materię.
Celem ćwiczenia było zbadanie, zależnie od grubości oraz rodzaju absorbentu, natężenia promieniowania gamma przechodzącego przez dany absorbent.
Wstęp Teoretyczny
Promieniowanie gamma- fala elektromagnetyczna emitowana przy przejściu jąder ze stanów wzbudzonych do stanów energetycznie niższych lub powstałą przy reakcjach jądrowych.
Promieniowanie przy przechodzeniu przez materię ulega osłabieniu. Osłabienie zależy wykładniczo
od grubości absorbentu i współczynnika osłabienia promieniowania gamma. Osłabienie promieniowania opisane jest wzorem:
I = I0 -μX
I - natężenie promieniowania po przejściu przez absorbent
X - grubość absorbentu
μ - współczynnik osłabienia promieniowania gamma
Zjawiska występujące przy przechodzeniu promieniowania gamma przez materię:
Efekt fotoelektryczny, w wyniku którego promieniowanie gamma oddaje energię elektronom, odrywając je od atomów lub przenosząc na wyższe poziomy energetyczne
Rozpraszanie comptonowskie - elektrony słabo związane lub swobodne doznają przyspieszenia w kierunku rozchodzenia się promieniowania. W pojedynczym akcie oddziaływania następuje niewielka zmiana energii kwantu gamma. W wyniku oddziaływania z wieloma elektronami kwant gamma wytraca swą energię. Jest to najważniejszy sposób oddawania energii przez promieniowanie gamma;
Tworzenie się elektron-pozyton - kwant gamma, uderzając o jądro atomowe, powoduje powstanie par cząstka-antycząstka (warunkiem zajścia zjawiska jest energia kwantu gamma > 1,02 MeV - dwukrotnej wartości masy spoczynkowej elektronu)
Przebieg ćwiczenia:
Jako pierwszy przeprowadziliśmy pomiar tła. Wykonaliśmy w tym celu 10 pomiarów bez wykorzystania pierwiastka promieniotwórczego. Przy pomocy komputera i specjalistycznego oprogramowania odczytaliśmy następujące wyniki:
Numer pomiaru |
Grubość Absrobenta [mm] |
N (liczba zliczeń) |
1 |
0 |
87 |
2 |
0 |
84 |
3 |
0 |
100 |
4 |
0 |
96 |
5 |
0 |
90 |
6 |
0 |
94 |
7 |
0 |
94 |
8 |
0 |
111 |
9 |
0 |
99 |
10 |
0 |
82 |
|
Nśr |
94 |
Średnia N = 94
uśr = ![]()
Następnie wykonaliśmy pomiary z aluminiowym absorbentem. W tym celu umieszczaliśmy w domku osłonowym coraz to grubsze płytki absorbentu. Otrzymaliśmy następujące wyniki:
Numer pomiaru |
Grubość Absrobenta [mm] |
Liczba zliczeń |
N |
Δ N |
ln N |
Δ (ln N) |
1 |
20 |
1528 |
1434 |
37,87 |
7,27 |
0,026 |
2 |
17 |
1709 |
1615 |
40,19 |
7,39 |
0,025 |
3 |
15 |
1692 |
1598 |
39,98 |
7,38 |
0,025 |
4 |
12 |
1720 |
1626 |
40,33 |
7,39 |
0,025 |
5 |
10 |
1838 |
1744 |
41,76 |
7,46 |
0,024 |
6 |
7 |
1898 |
1804 |
42,48 |
7,50 |
0,024 |
7 |
5 |
2009 |
1915 |
43,76 |
7,56 |
0,023 |
8 |
3 |
1982 |
1888 |
43,45 |
7,54 |
0,023 |
9 |
2 |
2025 |
1931 |
43,95 |
7,57 |
0,023 |
10 |
1 |
2134 |
2040 |
45,17 |
7,62 |
0,022 |
Do obliczenia poszczególnych elementów użyliśmy następujących wzorów:
N = Liczba zliczeń - Średnia N obliczona dla tła
Δ N = ![]()
Δ (ln N) = ![]()
Wykorzystując metodę najmniejszych kwadratów
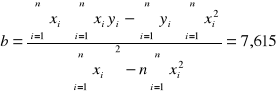
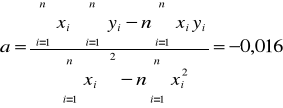
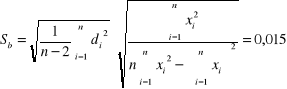
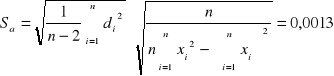
,
otrzymujemy następujące wyniki:
a +/- Sa = -0,016 +/- 0,0013 [1/mm]
b +/- Sb = 7,615 +/- 0,015
Kolejnym etapem było wykonanie tych samych pomiarów, z tym że wykorzystując absorbent wykonany z miedzi. Otrzymaliśmy następujące wyniki:
Numer pomiaru |
Grubość Absrobenta [mm] |
Liczba zliczeń |
N |
Δ N |
ln N |
Δ (ln N) |
1 |
20 |
763 |
669 |
25,87 |
6,51 |
0,039 |
2 |
17 |
972 |
878 |
29,64 |
6,78 |
0,034 |
3 |
15 |
1031 |
937 |
30,62 |
6,84 |
0,033 |
4 |
12 |
1197 |
1103 |
33,22 |
7,01 |
0,030 |
5 |
10 |
1251 |
1157 |
34,02 |
7,05 |
0,029 |
6 |
7 |
1471 |
1377 |
37,11 |
7,23 |
0,027 |
7 |
5 |
1643 |
1549 |
39,36 |
7,35 |
0,025 |
8 |
2 |
1800 |
1706 |
41,31 |
7,44 |
0,024 |
Do obliczenia poszczególnych elementów użyliśmy następujących wzorów:
N = Liczba zliczeń - Średnia N obliczona dla tła
Δ N = ![]()
Δ (ln N) = ![]()
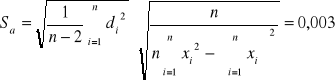
Wykorzystując metodę najmniejszych kwadratów
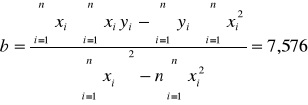
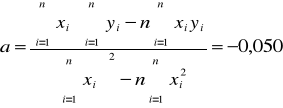
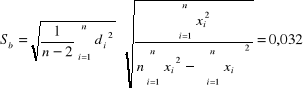
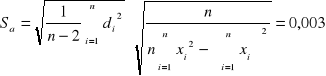
,
otrzymujemy następujące wyniki:
a +/- Sa = -0,050 +/- 0,003 [1/mm]
b +/- Sb = 7,576 +/- 0,032
Przedostatnim etapem naszego ćwiczenia było wykonanie tych samych pomiarów dla absorbentu wykonanego z ołowiu. Wyniki:
Numer pomiaru |
Grubość Absrobenta [mm] |
Liczba zliczeń |
N |
Δ N |
ln N |
Δ (ln N) |
1 |
20 |
272 |
178 |
13,35 |
5,18 |
0,075 |
2 |
17 |
363 |
269 |
16,41 |
5,60 |
0,061 |
3 |
15 |
494 |
400 |
20,01 |
5,99 |
0,050 |
4 |
12 |
599 |
505 |
22,48 |
6,23 |
0,044 |
5 |
10 |
727 |
633 |
25,17 |
6,45 |
0,040 |
6 |
7 |
984 |
890 |
29,84 |
6,79 |
0,034 |
7 |
5 |
1254 |
1160 |
34,06 |
7,06 |
0,029 |
8 |
2 |
1766 |
1672 |
40,89 |
7,42 |
0,024 |
Do obliczenia poszczególnych elementów użyliśmy następujących wzorów:
N = Liczba zliczeń - Średnia N obliczona dla tła
Δ N = ![]()
Δ (ln N) = ![]()
Wykorzystując metodę najmniejszych kwadratów
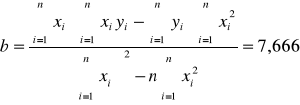
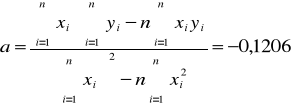
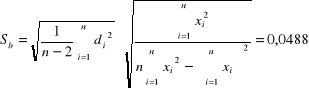
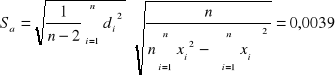
,
otrzymujemy następujące wyniki:
a +/- Sa = -0,1206 +/- 0,0039 [1/mm]
b +/- Sb = 7,666 +/- 0,0488
Wykonujemy 2 wykresy:
zależności natężenia promieniowania od grubości absorbentu
zależności logarytmu natężenia promieniowania od grubości absorbentu
Opracowanie wyników
I = I0 e-µ x
N = N0 e-µ x / * ln
ln N = ln N0 - µ x
ln N = - µ x + ln N0
y = - a * x + b
Wynika z tego iż współczynnik a i jego błąd równy jest współczynnikowi µ oraz jego błędowi. Otrzymane wyniki porównujemy z wynikami tablicowymi.
materiał |
energia cząstek [MeV] |
μ tablicowe |
μ doświadczalne |
Aluminium |
0,66 |
0,017 |
0,016 |
Miedź |
0,66 |
0,061 |
0,050 |
Ołów |
0,66 |
0,118 |
0,1206 |
Jak widać, wyniki otrzymane przez nas w trakcie ćwiczenia są zbliżone do tych tablicowych. Wskazuje to na poprawne wykonanie zleconego nam zadania.
Na podstawie wykonanych wykresów stwierdzić można, że zależność pomiędzy logarytmem naturalnym liczby zliczeń, a średnią grubością absorbentu przedstawia prosta y = ax + b.
Niedokładność pomiaru może wynikać z faktu iż w przypadku miedzi i ołowiu wykonano mniejszą ilość pomiarów (brak płytek o grubość 3 i 1 mm) oraz faktu iż każdy pomiar wykonywany był jednokrotnie.
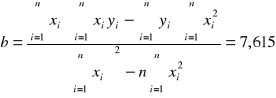
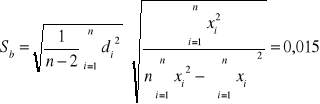
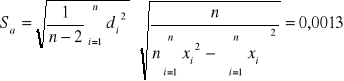
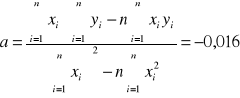
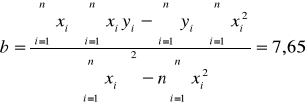
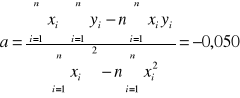
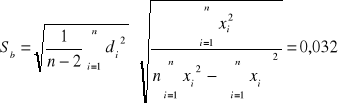
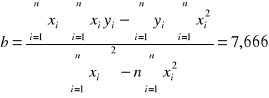
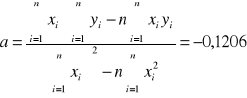
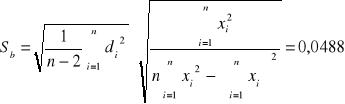
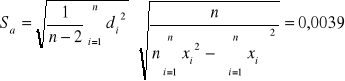
Wyszukiwarka
Podobne podstrony:
sprawko gamma, Laboratoria FIZYKA PW, 11 (Badanie osłabienia promieniowania gamma przy przechodzeniu
11 - sprawozdanie z promieniowania WM (2), Laboratoria FIZYKA PW, 11 (Badanie osłabienia promieniowa
Badanie osłabienia promieniowania Gamma przy przechodzeni przez materię final
Promieniotwórczość, badania oslabienia prom gamma, BADANIE OSŁABIENIA PROMIENIOWANIA GAMMA PRZY PRZE
Badanie osłabienia promieniowania gamma przy przechodzeniu przez materię 3
Sprawozdanie z ćw 11 Osłabienie promieniowania gamma przy przechodzeniu przez materię
lampa próżniowa sprw, Laboratoria FIZYKA PW, a27 (Badanie właściwości statystycznych elektronów emit
b11 ?danie osłabienia promieniowania przy przechodzeniu przez materię
dielektr, Laboratoria FIZYKA PW, c30 (odbicie światła od powierzchni dielektryka)
LAB 30C przyklad3, Laboratoria FIZYKA PW, c30 (odbicie światła od powierzchni dielektryka)
sprawmagicpo, Laboratoria FIZYKA PW, c30 (odbicie światła od powierzchni dielektryka)
FIZ2 11, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieniowania gamma przy pomo
sprawozadanie 11, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieniowania gamma
Sprawko w11 Mis, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieniowania gamma
FIZ11-Piter, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieniowania gamma przy
tomifizlab11, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieniowania gamma przy
sprawko -Promieniowanie gamma, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieni
cw11 florek, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieniowania gamma przy
sprawozdanie, MIBM WIP PW, fizyka 2, laborki fiza(2), 51-Badanie własności promieniowania gamma przy
więcej podobnych podstron