PODSTAWY TERMODYNAMIKI

I MECHANIKI PŁYNÓW

ORAZ WYMIANY CIEPŁA

Literatura:

1. J.Dowkon t :”Teoria silników cieplnych”WKŁ,1973r.

2. B Staniszewski :”Termodynamika” PWN,1977r.

3. J.Szargut:”Termodynamika”PWN,1980r.

4. S.Wiśniewski:”Termodynamika techniczna” WNT,1993r.

CHARAKTERYSTYKA PRZEDMIOTU

Termodynamika: Nazwa termodynamiki pochodzi od słów greckich (termos) ciągły i δυναμιξ (dynamis) siła i ma znaczenie historyczne. Ze względu na metody rozpatrywania zjawisk termodynamicznych termodynamikę dzielimy na: fenomenologiczną, statystyczną i relatywistyczną (kwantową).

Zadaniem przedmiotu termodynamiki technicznej jest przedstawienie obecnego i przyszłego poziomu stanu wiedzy w obszarze termodynamiki oraz przygotowanie studentów do analizowania i projektowania procesów cieplnych oraz stworzenie podstaw do studiów nad projektowaniem, doskonaleniem i eksploatacją maszyn i urządzeń energetycznych ze szczególnym uwzględnieniem tłokowych silników cieplnych. W ramach wykładów przedstawione są podstawowe zasady i prawa rządzące zjawiskami cieplnymi i przepływowymi, ilustrowanymi ćwiczeniami i przykładami liczbowymi. Podczas zajęć laboratoryjnych studenci zapoznają się z metodami pomiarów wielkości cieplnych i przepływowych. Koniecznymi wiadomościami z fizyki i chemii, znajomość rachunku różniczkowego, całkowego i równań różniczkowych. Wykorzystanie tego przedmiotu do innych przedmiotów to: wszystkie przedmioty w których rozważane są elementy procesów cieplnych i przepływowych oraz konstrukcji i eksploatacji silników cieplnych i innych maszyn oraz urządzeń energetyki cieplnej.

Krótki rys historyczny rozwoju termodynamiki.

Pojęcie klasycznej termodynamiki pojawiło się w 1824r w pracy francuskiego inżyniera S. Carnota pt. „Rozmyślania o poruszającej się sile ognia”, w której przedstawił on teorię maszyn cieplnych i wskazał drogi ich dalszego doskonalenia. W pracy tej obok zasadniczych pytań dotyczących teorii maszyn cieplnych przedstawiono pierwsze sformułowanie jednego z ważniejszych pojęć termodynamiki tzw. drugiej zasady termodynamiki.

Pojęcie to dopiero po upływie 30 lat zostało wykorzystane w pracach Clausiusa, który przedłużał naukę o drugiej zasadzie termodynamiki. Tek więc Carnote'a swoją w/w pracą dał początek rozwoju termodynamiki klasycznej. Należy tu zaznaczyć, ze nauka o cieple pojawiła się w fizyce znacznie wcześniej. Jednak z tym nie wiążemy rozwoju termodynamiki, ponieważ w tych epokach rozwoju fizyki ciepła, ciepło rozpatrywano jako nieważką ciecz nazywaną cieplikiem.

Dalszym ważnym etapem rozwoju termodynamiki są prace 40- 50 lat XIX wieku, związane z formułowaniem pierwszej zasady termodynamiki, która w nauce pojawiła się później niż druga zasada termodynamiki. Pierwsza zasada termodynamiki przedstawiająca sobą wyrażenie w ogólnej postaci zasady zachowania energii, związana jest z pracami trzech badaczy, którzy z różnych punktów widzenia podchodzili do formułowania tego podstawowego prawa przyrody.

W 1842r niemiecki lekarz R. Mayer w pracy pt. „Rozmyślania o siłach nieożywionej przyrody” odniósł się do tych problemów. Praca ta nie spotkała się z szerszym zainteresowaniem większości uczonych. W 1847r została wydana monografia przez niemieckiego lekarza G. Welmholtza - późniejszego wielkiego fizyka i filozofa pod tytułem: „O zachowaniu siły”. W latach od 1843 do 1856 Joule'a w Anglii badał eksperymentalnie mechaniczny współczynnik ekwiwalentny ciepła wyrażający sobą ilość energii mechanicznej, która jest ekwiwalentem ilości zamienionego na nią ciepła (wyrażony w kilokaloriach).

W monografii Helmholtza wskazuje się i podkreśla ogólne znaczenie pierwszej zasady termodynamiki, podaje się jej matematyczne sformułowanie i rozpatruje się duża liczbę różnych zastosowań w fizyce.

Prace Joule'a pokazały stałość i wielkości mechanicznego ekwiwalentu ciepła w różnorakich procesach przemiany energii i tym samym opracowały eksperymentalną tezę zgodną z zasadą zachowania energii.

Rozdzielenie pojęć „energia” i „siła” następowało stopniowo podczas rozwoju mechaniki. Jeszcze Leibniz rozróżniał „żywą siłę” od innych postaci sił, chociaż ta „żywa siła” ma wymiar energii (my nazywamy ją energią kinetyczną) wcześniej w mechanice nie posługiwano się różnym pojęciem energii. Termin „energia” spotyka się jeszcze w pracach Arystotelesa, później używali go Kepler, Galileusz, Leibniz- ale nie wiązali z nim dokładnej definicji. Zwróćmy uwagę, ze już praca Helmholtza gdzie rozpatruje się zachowanie energii, była zatytułowana „O zachowaniu siły”. Jasno wyrażają ideę zasady zachowania można spotkać w pracach Łomonosowa, Deckerta i innych.

Wszystkie te bardzo ogólne sformułowania nie mogły służyć do dokładnego ustalenia i sformułowania pierwszej zasady termodynamiki.

Kolejny rozwój drugiej zasady termodynamiki znajdujemy w szeregu pracach Clausiusa (1850-1876r), w których podano klasyczne sformułowania drugiej zasady termodynamiki, oraz postawiono pierwsze kroki w rozwoju molekularnej teorii. W pracach Clausiusa po raz pierwszy wprowadza się ważne pojęcie w termodynamice „entropia” i rozpatruje się jej własności. Do tego okresu - połowa XIX wieku należą prace w. Thomsona (Kelvina) i Maxwella, gdzie podaje się nowe sformułowania zasad termodynamiki, uściśla się pojęcie temperatury, wprowadza się absolutną skalę temperatur i po raz pierwszy wprowadza się pojęcie tzw. charakterystycznych funkcji termodynamicznych.

W końcu w pracach Baltzmanna i szczególnie Gibasa z drugiej połowy XIX wieku podaje się podstawy termodynamiki statystycznej.

Rozwój tego współczesnego nam kierunku jest mocno związany ze stopniowym formułowaniem kinematyczno- molekularną teorią opartą o prace w/w uczonych. Jednocześnie z opracowaniem podstaw termodynamiki klasycznej wzrastają prace dotyczące ich zastosowania technice cieplnej, chemii fizycznej, teorii promieniowania, w astrofizyce itd.

Największy rozwój termodynamika klasyczna osiągnęła w pracach Gibasa, który kolejno posługuje się funkcjami termodynamicznymi, po raz pierwszy formułuje zasadę reguły faz, podaje podstawy termodynamiki chemicznej oraz odgrywa ważną rolowe współczesnej chemii fizycznej. Na początku XX wieku Zemst formułuje trzecią zasadę termodynamiki i tworzy teorię zachowania się systemów (układów) termodynamicznych w pobliżu zera absolutnego.

M. Planch i W. Ostwald systematyzują wyniki rozwoju termodynamiki klasycznej i rozpatrują szereg ważnych jego zastosowań. Najnowszy rozwój termodynamiki w zasadzie opiera się na fizyce statystycznej, chociaż istnieje kierunek „ czystej termodynamiki” aksjomatyczną.

PODSTAWOWE POJĘCIA I OKREŚLENIA

1. Wprowadzenie.

Termodynamika wchodzi do obszaru makrofizyki i obecnie można ją podzielić na: termostatykę i na termodynamikę.

Termostatyka zajmuje się własnościami systemów makroskopowych, znajdujących się w równowadze termodynamicznej. Jest ona najbardziej rozwiniętą gałęzią termodynamiki. Zajmuje się systemami, które praktycznie nie zmieniają się w czasie analogicznie do rozdziału statyki w mechanice i dlatego często nazywa się ja termostatyką. Z termostatyką związane są podstawowe prawa fizyki i na jej podstawie wyrosła chemia fizyczna. Szeroko wykorzystywana jest w wielorakich obliczeniach technicznych (tzw. termodynamiki technicznej) realizowanych przy projektowaniu większości maszyn cieplnych.

Jednak współczesna technika wymaga badania własności i zachowania się makrosystemów w skończonym i bardzo krótkim czasie. Na przykład procesy zachodzące podczas wyrzutu rakiety, szybko zachodzące procesy we współczesnej technologii z udziałem katalizatorów lub reaktorów atomowych, nie mogą być niezawodnie opisane tylko za pomocą równań termostatyki. Obecnie brak takich równań i dlatego otrzymywane dane nie mogą opisywać przebiegu procesów zachodzących w funkcji czasu. Dlatego też ostatnio szybko rozwijana jest teoria tzw. procesów nierównowagowych, zachodzących w makrosystemach, będące termodynamiką nierównowagową, którą co do jej istoty należy nazywać termodynamiką badającą procesy zachodzące w czasie.

W starszych programach fizyki różnie rozpatrywano termostatykę i jej nauczanie o przekazywaniu ciepła, które zgodnie ze współczesnym punktem widzenia odnoszą się do termodynamiki. W realizowanym przez nas programie będziemy zajmować się przede wszystkim termostatyką. Ponieważ ma ona największe znaczenie ogólnie we wszystkich działach fizyki i dlatego bez badania termostatyki nie można przyswoić sobie zagadnień termodynamiki procesów nierównowagowych.

2. Zadania termodynamiki. Zerowa zasada termodynamiki. Fenomenologia.

Rozważmy nieco dokładniej to, co będziemy rozumieć pod pojęciem mikrofizyki.

We współczesnej fizyce zwykle rozróżnia się przede wszystkim fizykę mikrocząsteczki: elektronów, protonów, atomów, cząstek i fotonów-nazywaną mikrofizyką w odróżnieniu od ciał makroskopowych (lub systemów ) składających się z ogromnej liczby mikrocząsteczek , która odpowiednio nazywa się makrofizyką. Makrociała tworzą ogromne liczby ∼10²⁰÷10²⁵ cząstek. Taka liczba cząstek w makrociałach jest na tyle duża, że nie ma możliwości badać zachowanie się oddzielnej cząstki i dlatego wygodnym jest stosowanie statystycznych metod, które przedstawiają sobą bardzo szeroki obszar zwany fizyką statystyczną. Można jednak spisywać wiele właściwości makrociał odchodząc od molekularnej ich budowy, a uwzględniając tylko zachowanie się systemu jako całości, podobnie jak się to czyni w wielu zadaniach mechaniki, np. w mechanice ośrodków ciągłych. Tą drogą idzie termodynamika, która różni się od tzw. termodynamiki statystycznej, gdzie rozpatruje się właściwości makrociał (warunkowanych) zależnych od ruchu i oddziaływania wzajemnego poszczególnych cząstek i innych mikrocząstek.

Zwykła termodynamika klasyczna rozumie ruch cząstek jako wyrażany temperaturą. Pogląd ten jest na tyle ważny, że niekiedy nazywa się go zerową zasadą termodynamiki, aby podkreślić, że zasadnicze znaczenie takiej przesłanki formułuje się w postaci aksjomatu: wszystkie ciała przy równowadze cieplnej charakteryzują się temperaturą.

Ponieważ molekularny ruch cieplny jest podstawowa własnością wszystkich ciał materialnych, to zerową zasadę termodynamiki należy traktować jako fundamentalny stan wyjściowy termodynamiki, ponieważ każde ciało charakteryzuje temperatura, która może być zmierzona eksperymentalnie.

W mechanice klasycznej temperatura nie jest uwzględniana i tym różni się ona od termodynamiki opartej mianowicie na zerowej zasadzie termodynamiki. Można zatem traktować, że mechanika klasyczna opisuje ruch i własności ciał ( i systemów) przy absolutnym zerze temperatury.

Pozwala to określić podstawowe zadania termodynamiki jako nauki, w której bada się własności ciał makroskopowych a także procesy zachodzące w tych ciałach, z uwzględnieniem tego, że ciała te zawsze charakteryzują się temperatura zmierzona. Podczas badanie zjawisk zwracamy uwagę wyłącznie na makroskopowe własności systemu, które oceniamy według danych doświadczalnych otrzymanych z pomiarów za pomocą makroskopowych przyrządów: termometrów, kalorymetrów, nanometrów itp. dlatego też termodynamika klasyczna jest nauką fenomenologiczną (od słowa-„fenomen” - zjawisko).

Nie zajmuje się ona i nie opiera się ona na żadnych hipotezach, które nie byłyby związane z „grubymi” zjawiskami makroskopowymi.

Nie patrząc na duże znaczenie i opisanie wielorakich zjawisk oraz wiele sformułowanych wniosków ogólnych, klasyczna fenomenologiczna termodynamika nie jest wystarczająca i jasna z punktu widzenia fizyki współczesnej.

Fenomenologiczne podejście do zjawisk stosowane w termodynamice nie można uznać jako istotny niedostatek tej nauki, szczególnie wówczas, gdy nie ma konieczności zajmowania się szczegółowym badaniem makroskopowych szczegółów zjawiska. Jako przykład może tu być wyznaczenie sprawności maszyn cieplnych-nie trzeba tutaj rozpatrywać ruchu i oddziaływania wzajemnie między cząsteczkami tworzącymi czynnik roboczy, czy też zderzeń cząstek ze ściankami cylindra, powstanie nowych cząstek np. na skutek reakcji chemicznych itp.

Z podobnymi metodami fenomenologicznymi mamy do czynienia np. w hydrostatyce, hydrodynamice, mechanice itd.

W obszarach tych również nie interesuje nas cząsteczkowa budowa ośrodka realizującego odpowiedni proces.

2.1. Metody stosowane w termodynamice.

• Fenomenologiczne-układy termodynamiczne ii zachodzące w nich zjawiska opisuje się za pomocą związków między wielkościami fizycznymi, które można sprawdzić doświadczalnie. Nie opisują wewnętrznej budowy substancji.

• Statystyczne-rozpatrują zbiory dużych liczb cząstek tworzących daną substancje. Metody te cechuje ogólność i możliwość ich eksperymentalnego sprawdzenia. Są one dość proste i pozwalają na głębszą interpretacje pojęć i praw termodynamiki.

• Relatywistyczne-stosują prawa fizyki kwantowej i teorii względności.

Problemy termodynamiki fenomenologicznej obejmują:

—stan termodynamiczny;

—bilanse: substancji, pędu, energii, entropii, egzergii;

—warunki równowagi i stabilności równowagi termodynamicznej;

—przemiany fazowe;

—reakcje chemiczne;

—przemiany i obiegi (cykle) termodynamiczne;

—procesy równowagowe;

—termodynamikę przepływów ściśliwych;

—zjawiska elektryczne i magnetyczne;

—otrzymywanie niskich temperatur;

—teorię roztworów;

—zjawiska powierzchniowe;

Termodynamika ta oparta jest na czterech podstawowych prawach empirycznych zwanych zasadami termodynamiki traktowanymi jako aksjomaty w oparciu o które wprowadza się dużą liczbę praw i zależności stanowiących obszerne działy termodynamiki.

• Zerowa zasada termodynamiki—wprowadza pojęcie temperatury i równowagi termicznej

• Pierwsza zasada termodynamiki—wprowadza pojęcie energii wewnętrznej oraz definiuje ciepło.

• Druga i trzecia zasada termodynamiki—wprowadza pojecie entropii.

Podział termodynamiki fenomenologicznej:

1. Termodynamika stanów równowagi (termostatyka)-zajmuje się zjawiskami rozpatrywanymi jako zbiory kolejnych stanów równowagi. Rozpatruje również stany skrajnej równowagi między którymi mogą zachodzić zjawiska nierównowagowe.

2. Termodynamika procesów nierównowagowych-rozpatruje zjawiska, które nie przebiegają przez stany równowagi.

3. Termodynamika techniczna-zajmuje się zjawiskami wykonywania pracy mechanicznej kosztem doprowadzania ciepła oraz sporządzaniem bilansów: ilości substancji, energii, entropii i egzergii. Włączenie do niej elementów wymiany ciepła i teorii spalania powoduje, że staje się ona podstawą takich nauk stosowanych jak: teoria maszyn i silników cieplnych, gospodarka energetyczna, teoria chłodnictwa, teoria aparatury przemysłu chemicznego i spożywczego.

4. Termodynamika chemiczna-stosowana do opisu zjawisk w których występują reakcje chemiczne.

2.2.Materia i jej cechy oraz układ termodynamiczny.

Substancja-jest to materia o budowie korpuskularnej i o masie różnej od zera.

Materia substancjonalna-w fizyce jest to pojęcie pierwotne określające wszystkie obiekty ważkie tzn. wytwarzające pole grawitacyjne i podlegające działaniu tego pola.

Materia nie substancjonalna - są to różnego rodzaju pola sił np. pole grawitacyjne, elektromagnetyczne, zbiór kwantów itp.

Układ fizyczny-jest to materia ograniczona pewnym obszarem.

Układ termodynamiczny-jest to obszar materii ograniczonej osłoną kontrolna materialna lub abstrakcyjną. Układ ten może być:

—zamknięty-przez powierzchnie kontrolne nie może być wymieniana substancja,

—otwarty-przez powierzchnie kontrolne może być wymieniana substancja.

Rodzaje powierzchni kontrolnych:

• przepuszczalne dla substancji i energii,

• półprzepuszczalne dla wybranego elementu układu,

• diatermiczne—nie przepuszczają substancji, a przepuszczają ciepło,

• adiabatyczne—nie przepuszczają substancji i ciepła zaś mogą wymieniać pracę.

Układ odosobniony-nie wymienia substancji i energii.

Otoczenie-wszystko to co jest poza układem.

Parametry stanu-są to wielkości stałe lub zmienne (nie zależne od historii układu) charakteryzujące stan rozpatrywanej substancji, powiązane ze sobą równaniem stanu. Zmiana jednego z nich zmienia stan układu.

Parametry termodynamiczne układu-są to np. wielkości p,V,T,M, których zmiana istotnie zmienia analizowane zjawisko termodynamiczne.

Parametry te mogą być:

—ekstensywne-wartości ich zależą o ilości substancji (parametry te odniesione do jednostki ilości substancji stają się parametrami intensywnymi np. objętość właściwa
),

—intensywne-ich wartości nie zależą od ilości substancji(p,υ,T, ciepło parowania L itp.).

Stan termodynamiczny układu-jest zbiór jednoczesnych wartości wielkości zdolnych do zmiany wielkości fizycznych zwanych parametrami stanu.

Funkcja stanu-jest to funkcja zależna od parametrów stanu układu.

2.3.Zasada zachowania energii:

Energia nie może znikać ani samoistnie powstawać. Może tylko zmieniać postać przy jej stałym zasobie.

Energia może być: mechaniczna, cieplna, chemiczna, jądrowa itp.

2.4. Podstawowe wielkości fizyczne i ich jednostki.

Wielkości fizyczne służą do wyrażania praw fizyki. Aby zdefiniować wielkość fizyczną należy ustalić sposób postępowania tzn. receptę mierzenia tej wielkości oraz przyjąć jednostkę tej wielkości. Ze względu na dużą ilość wielkości fizycznych zachodzi potrzeba ich uporządkowania. Wielkości te nie są wcale niezależne względem siebie, np. prędkość jest stosunkiem długości do czasu. Dlatego też, spośród wszystkich możliwych wielkości fizycznych wybiera się tylko niezależne wielkości, które nazywamy wielkościami podstawowymi, natomiast wszystkie pozostałe wielkości nazywamy wielkościami pochodnymi.

Każdej wielkości podstawowej przyporządkowuje się wzorzec.

Ilość wielkości podstawowych wybiera się jako najmniejszą ilość(liczbę) wielkości fizycznych, która umożliwia kompletny opis fizyki za pomocą najprostszych pojęć. Wyboru wielkości podstawowych dokonuje Międzynarodowe Biuro Miar i Wag -pod Paryżem-założone w 1875r. Ostatnia Konferencja Biura Miar i Wag odbyła się w 1971r.(czwarta).

Konferencja ta wybrała siedem jednostek podstawowych tj.: długość , m; masa, kg; czas, s; prąd elektryczny, A; temperatura, K; liczność materii, mol; światłość, cd (kandela).

2.4.1. Ilość substancji.

Jednostką ilości substancji w termodynamice jest 1 mol.

Masa kilomolowa-masa 1 mol substancji, jest to tyle kilogramów substancji ile wynosi jej masa cząsteczkowa.

1 kmol substancji zawiera (6,0268±0,00016)*10²⁶ cząsteczek, to jest tyle cząsteczek ile zawiera 12 kg izotopu węgla ¹²C.

Zasada zachowania ilości substancji -w zjawiskach fizycznych liczba cząsteczek nie zmienia się oraz nie zmienia się liczba atomów podczas reakcji chemicznych.

Liczba Avogadra N_A-jest to liczba (6,0268±0,00016)*10²⁶.

W równaniu stechiometrycznym reakcji chemicznych ilość atomów lewej strony równania równa się ilości atomów prawej strony równania. Ilość kilomoli znajdujących się w 1 kg substancji jest odwrotnością jej masy (gęstości) kilomolowej, np. 1 kg wodoru zawiera

Ilość cząsteczek w układzie jest:

N=n*N_A

Masa-jest to właściwość układów fizycznych określająca ich bezwładność (masa bezwładna) lub oddziaływanie grawitacyjne (masa grawitacyjna).

Masa bezwładna (ΙΙ z. Dynamiki Newtona) jest miarą bezwładności oporu ciała jaki ono stawia przy zmianie stanu jego ruchu.

F=m*a

Relatywistyczna zmiana masy-jest ekwiwalentem zmiany energii E=mc² gdzie

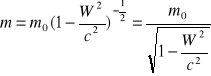
m₀-masa spoczynkowa.

2.4.2. Objętość—objętość skończonej ilości substancji nigdy nie może przybierać wartości równej zeru.

Objętość gazu ograniczają ścianki naczynia zamkniętego, w którym się on znajduje. Jeśli wszystkie części ciała znajdują się w tych samych warunkach, to możemy rozpatrywać tylko część tego ciała np. 1 kg o objętości właściwej:

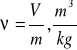
lub

Normalny metr sześcienny nm³-jest to ilość substancji zawarta w objętości 1 m³ w normalnych warunkach fizycznych tzn. w temperaturze T=273 K i przy p=1atm=760mmHg=101325 Pa.

2.4.3. Ciśnienie- jest to stosunek siły F wywieranej na powierzchnię do pola tej powierzchni A, tj.

, (1)

W sensie statystycznym-ciśnienie jest miarą wymiany pędu między cząsteczkami znajdującymi się w ruchu termicznym:

gdzie: N_ν-liczba cząsteczek w objętości jednostkowej ν;

-średnia energia kinetyczna drobiny.

Pomiaru ciśnień wyższych od ciśnienia atmosferycznego dokonuje się manometrami wskazującymi ciśnienie p_m

Ciśnienie bezwzględne jest:

p=p_at+p_m (2)

Pomiaru ciśnień niższych od atmosferycznego dokonuje się wakumetrami (podciśnieniomierze). Wskazują one wartość p_W a ciśnienie bezwzględne oblicza się z:

p=p_at-p_W (3)

kkkkkkkkkkkkk

Rys.1. Rodzaj ciśnień

Jednostką ciśnienia jest
; 1 MPa=10⁶ Pa; 1 bar=10⁵ Pa≈0,091 MPa

Nadciśnienie mierzone wysokością słupa cieczy:

qqqqqqqqqqqqqq

p+zgρ=p_ot+zgρ_c⇒p-p_ot=p_m=zg(ρ_c-ρ);

p_m=p- p_ot=zg(ρ_c-ρ) (4)

z-wysokość cieczy manometrycznej ;

ρ_c-gęstość cieczy manometrycznej;

ρ-gęstość płynu, którego ciśnienie mierzymy.

Podciśnienie mierzone słupem cieczy manometrycznej:

ddddd

p+zgρ_c= p_ot+ zgρ_ot , stąd

p_W= p_ot-p= zg(ρ_c-ρ_ot); (5)

p_ot-gęstość powietrza atmosferycznego

Inne jednostki ciśnienia:

1 Tr=133,3224≈133,3 Pa

Ciśnienie jednej atmosfery fizycznej (warunki normalne):

P_n=1 atm=760 Tr=101325 Pa=0,101325 Mpa

2.4.4. Temperatura, K, °C

Jest pojęciem pierwotnym i podstawowym-nie definiowana za pomocą innych wielkości. Temperatura określa stopień nagrzanie ciała, odróżnia ciało cieplejsze od zimniejszego oraz umożliwia opis analityczny przepływu ciepła.

Rozróżniamy następujące skale temperatur: skala bezwzględna, skala Celsjusza, skala Farenheita, Reomiura i skala Rankine′a oraz skala praktyczna.

Skala bezwzględna-
temperatury potrójnego punktu wody(T₀=273,16 K; p=611,2 Pa)

Skala Celsjusza-
podziału między punktami wrzenia i krzepnięcia wody.

Zależności miedzy różnymi skalami temperatury

Nazwa skali	Skala Celsjusza t,°C	Skala Reankina T,°Ra	Skala Farenheita t, °F	Skala Reamiura, t,°R
Skala Celsjusza,°C	—	T°Ra-273,16		1,25 t°R
Skala Reankina,°Ra	1,8(t°C+273,16)	—	T °F+459,67	1,8(1,25t°R+273,16)
Skala Farenheita, °F	1,8 t°C+32	T°Ra-459,67	—	t°R+32
Skala Reamiura, °R	0,8 t°C	0,8( T°Ra-273,16)	( t °F-32)	—

Skala praktyczna temperatury-oparta jest o 11 punktów: krzepnięcia, wrzenia i punktów potrójnych różnych substancji.

Pomiar temperatury: mierzy się ją wykonując temperaturowe zmiany własności substancji (ν,p,α).

Według kinetyczno-molekularnej teorii, temperatura jest miarą średniej energii kinetycznej postępowego ruchu drobin (wzrost temperatury powoduje zmianę faz; zmniejszenie energii powoduje zanik ruchu, gdy T→0).

2.5.Zerowa zasada termodynamiki (zasada tranzytywności (przejścia) równowagi termodynamicznej).

Jeżeli:

ddddddddddd

Jeżeli układy A i B są w równowadze termicznej i równocześnie układy B i C są również w równowadze termicznej, to także układy A i C są w równowadze termicznej.

Sformułowanie słowne zerowej zasady termodynamiki:

Jeżeli spośród trzech układów A, B i C znajdujących się w stanie wewnętrznej równowagi termodynamicznej, każdy z układów A i B jest w równowadze termicznej z układem C, to układy A, B i C są ze sobą w równowadze termicznej (mają tę samą temperaturę).

Sformułowanie to podał J.C. Maxwell i zostało ono nazwane zerową zasadą termodynamiki.

2.6. Prawo Richmanna i doświadczenie Joule'a.

Prawo Richmanna (prawo bilansu cieplnego) brzmi: ilość ciepła oddana przez ciało jest równa ilości ciepła pobranego przez ciała otaczające. Wynika z niego wniosek: ilość ciepła pobrana przez ciało podczas ogrzewania jest równa ilości ciepła oddanego podczas jego ostygania w tym samym zakresie temperatur, jeśli ciało przechodzi w odwrotnym porządku przez te same stany pośrednie.

Doświadczenie Joule'a- na jego podstawie wyznaczono cieplny równoważnik pracy mechanicznej: 1 kcal=427 kGm.

W oparciu o to doświadczenie sformułowano ważne prawo Joule'a: praca sił tarcia jest ciepłem.

Pracę można całkowicie zmienić na ciepło, ale odwrotnie ciepło na pracę tylko częściowo. Lepkość materii powoduje istnienie pracy tarcia, a ta jest ciepłem.

3. CZYNNIK TERMODYNAMICZNY.

Czynnik termodynamiczny- jest to substancja biorąca udział w procesach termodynamicznych.

3.1. Prawo gazu doskonałego (idealnego) i termiczne równanie gazów doskonałych i półdoskonałych.

Gaz doskonały (idealny)-jest to hipotetyczny gaz, którego drobiny nie przyciągają się wzajemnie, są nieskończenie małe i sztywne (tzn. wewnątrz drobin nie występują drgania oraz zgodnie z kinetyczno-molekularna teorią i doświadczeniem gaz ten w rozumieniu termodynamicznym nie jest pozbawiony lepkości-nie tak jak w hydromechanice, gdzie płyn doskonały definiuje się jako płyn nie lepki).

Gaz półdoskonały-w odróżnieniu od gazu doskonałego, w drobinach tego gazu występują drgania, a zatem atomy w cząsteczce powiązane są ze sobą sprężyście.

Stan czynnika roboczego i prawa gazu doskonałego.

Stan czynnika termodynamicznego określają termiczne parametry stanu: ciśnienie, temperatura i objętość właściwa.

Dla czynnika jednorodnego tylko dwa spośród tych trzech parametrów są niezależne, trzeci zaś jest jednoznacznie określony za pomocą równania stanu.

Prawo Boyle'a i Mariotte'a: (w 1662 r. Boyle'a a w 1676 r. Mariott) wykazali, że przy stałej ilości gazu doskonałego (stała objętość właściwa) i przy stałej temperaturze iloczyn ciśnienia przez objętość gazu jest wielkością stałą:

p*V=const.

Prawo Gay-Lussaca: w 1802 r. Gay-Lussac wykazał, że przy stałej ilości gazu i stałym ciśnieniu, objętość gazu podczas jego ogrzania wzrasta ze wzrostem temperatury zgodnie z zależnością liniową w postaci:

V=V₀(1+αt)

gdzie:

V-objętość gazu przy temperaturze t°C,

α-temperaturowy współczynnik rozszerzalności objętościowej gazu równy

Dokładnie

Wyprowadzenie równania stanu gazu doskonałego.

Termiczne równanie stanu gazów doskonałych wynika ze znanych praw empirycznych fizyki: Boyle'a i Mariotte'a oraz prawa Gay-Lussaca.

Rozważmy dwa dowolnie położone punkty na wykresie współrzędnych p-υ, odpowiadające stanom 1 i 2 oraz pomocniczy punkt 3, będący przecięciem izobary przechodzącej przez punkt 1 oraz linii stałej temperatury (hiperbola równoosiowa) przechodzącej przez punkt 2.

Dasddd

Rys.2. Wykres pomocniczy do wyprowadzenia równania stanu gazów doskonałych.

Z prawa Gay-Lussaca dla stanów 1 i 3 wynika, że :

ponieważ T₂=T₃ (1)

Z prawa Boyle'a i Mariotte'a dla stanów 2 i 3, przy uwzględnieniu, że p₃=p₁ jest:

p₁ν₃=p₃ν₃=p₂ν₂ (2)

Zrównania (1) mamy:
.Wykorzystując tą zależność w równaniu (2) otrzymamy:

(3)

Równanie (3) jest równaniem Clapeyrona dla jednego kilograma gazu doskonałego, który możemy zapisać w postaci:

pν=RT (4)

gdzie: R- jest indywidualną stałą gazową wyrażoną w
.

W ujęciu fenomenologicznym gaz doskonały definiuje się jako gaz spełniający równanie stanu Clapeyrona.

Mnożąc równanie (4) przez m otrzymujemy:

pνm=mRT czyli pV=mRT (5)

Rozważmy równanie Clapeyrona dla dwóch stanów gazu o masie m:

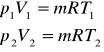
stąd otrzymujemy:

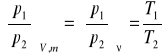
(6)

Równanie (6) przedstawia sobą prawo Charlesa: przy stałej objętości i stałej ilości (lub stałej objętości właściwej) ciśnienia bezwzględne gazu doskonałego są wprost proporcjonalne do temperatury bezwzględnej.

Precyzyjne eksperymenty wykazały, że w rzeczywistości zachowanie się gazów nawet przy wysokich ciśnieniach odbiega nieco od równania (4). Jednak im mniejsza gęstość gazu, tym dokładniej równanie (4) opisuje jego zachowanie się. Gaz rzeczywisty ma tym bliższe właściwości, właściwością gazu doskonałego im mniejsza jest jego gęstość.

Równanie (4) wyprowadzić można również metodą kinetycznej teorii gazów (fizyka) jeżeli założyć, że cząsteczki gazu są punktami materialnymi nie przyciągającymi się wzajemnie.

Sens wprowadzenia pojęcia gazu doskonałego.

1.Ponieważ w praktyce często mamy do czynienia z gazami pod niewysokimi ciśnieniami i dokładność obliczeń technicznych różnych procesów zachodzących w gazach jest zupełnie wystarczająca jeśli są one przeprowadzane z zachowaniem równania stanu gazu doskonałego.

2.Pojęcia dotyczące gazu doskonałego i praw jego zachowania są potrzebne i wystarczające do opisu spotykanych w praktyce zakresach, praw zachowania się gazu rzeczywistego. Są one ważne ze względów metodycznych i praktycznych np. obliczenia ciepła właściwego gazów rzeczywistych.

3.2. Prawo Avogadra i wynikające z niego wnioski.

Prawo Avogadra (sformułowane w 1811 r.):

W różnych objętościach, różna gazy doskonałe znajdujące się w jednakowych temperaturach i przy jednakowych ciśnieniach zawierają równe liczby cząsteczek.

Rozważmy dwa gazy oznaczając ja symbolami I i II.

AAAAAAAAAA

Ilość gazu m wyrażoną w kilogramach można obliczyć jako iloczyn liczby

cząsteczek N przez ich masę cząsteczkową μ_C lub jako iloczyn liczby kilomoli n przez masę kilomolową M_μ:

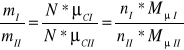
(7)

Ponieważ masy molowe są wprost proporcjonalne do mas cząsteczkowych gazów tj.

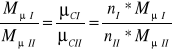
, a zatem n_I=n_II=n

Przy jednakowych ciśnieniach i temperaturach, w jednakowych objętościach zawarte są jednakowe liczby ich kilomoli.

Wniosek ten wiąże się ze stwierdzeniem, że 1 mol dowolnego gazu doskonałego zawiera ściśle określoną liczbę cząsteczek tzn. liczbę Avogadra (wg skali ¹²C)

N_A=(6,0268±0,00016)*10²³
(8)

Ilość gazu m w kilogramach obliczyć można również za pomocą iloczynu objętości V przez gęstość substancji ρ tj.:

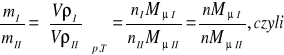
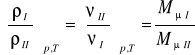
(9)

Przy jednakowych ciśnieniach i jednakowych temperaturach gęstości gazów doskonałych są wprost proporcjonalne, a objętości właściwe odwrotnie proporcjonalne do ich mas cząsteczkowych.

Z (9) wynika, że przy p=const, T=const jest:

ν_I M_μI=ν_II M_μII =ν M_μ=V_μ=const (10)

Przy jednakowych ciśnieniach i jednakowych temperaturach objętości molowe różnych gazów doskonałych są jednakowe.

W przypadku szczególnym tj. w normalnych warunkach fizycznych (T_n=273,16 K; p_n=1 atm=101325 Pa) objętość molowa każdego gazu doskonałego jest:

czyli (11)

1kmol=22,4135 m _n³

Obliczyć tą objętość np. dla tlenu:
; a objętość właściwa obliczona wg równania Clapeyrona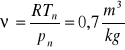
.

Wówczas:

Gęstość gazu doskonałego w fizycznych warunkach normalnych jest:

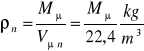
Rozważmy równanie Clapeyrona dla dwóch gazów doskonałych I i II przy p=const i T=const.

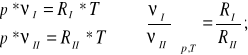
(12)

Uwzględniając (9) i zależność (12) można napisać:

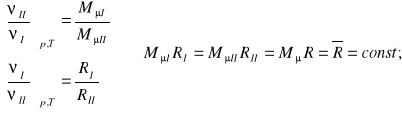
(13)

Uniwersalna stała gazowa
odniesiona do kilomola jako jednostki ilości substancji ma wartość jednakową dla wszystkich gazów doskonałych (wg. Skali ¹²C).

(14)

Uwzględniając, że M_μ*R=
i V=ν*m=n*M_μ,

równanie (4) można zapisać:

pν=RT /*m ⇒pνm=Mrt

(15)

gdzie:ν_μ- molowa objętość właściwa.

3.3 Gazy rzeczywiste.

Substancje mogą występować w różnych stanach skupienia i w różnych fazach różniących się parametrami i właściwościami fizycznymi. Stan termodynamiczny jednoskładnikowych faz substancji można przedstawić na wykresie we współrzędnych p-T.

SAKLDHCAVN

Rys.3. Wykres stanów faz wody, we współrzędnych p-T.

W stanie krytycznym i nadkrytycznym nie ma możliwości ani potrzeby odróżnienia stanu ciekłego od lotnego.

Para o temperaturze wyższej od temperatury nasycenia przy tym samym ciśnieniu jest nzw. parą przegrzaną.

Gaz doskonały o gaz rzeczywisty.

Model gazu doskonałego spełnia równanie stanu Clapeyrona. Przyjęcie ciepła właściwego za stałą pozwala na łatwe analityczne przedstawienie i rozpatrywanie bilansu energetycznego gazu. Model ten nie obejmuje zmian stanu skupienia. Tylko niektóre gazy techniczne i to w szczególnych warunkach mogą być opisane równaniem Clapeyrona.

Vcvc

Rys.4. Izoterma T_n=273 K dla 1 kmola gazu doskonałego (hiperbola równoosiowa).

Dla gazów rzeczywistych w miarę spadku temperatur przemiany stają się nieregularne, a poniżej temperatury krytycznej mają załamania, np. izobara Gay-Lussaca we współrzędnych T-ν:

Dmskf

Rys.5. Izobara Gay-Lussaca w układzie T-ν dla gazu rzeczywistego.

Stan gazów rzeczywistych w praktyce przedstawia się w postaci eksperymentalnie sporządzonych wykresów lub tablic liczbowych.

W niektórych przypadkach posługujemy się równaniami stanu gazów rzeczywistych:

1. Równanie Van der Walsa:

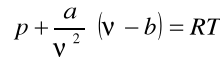
(16)

gdzie:
-ułamek poprawkowy uwzględniający siły spójności (normalne);

b- wielkość uwzględniająca wpływ objętości cząstek

2. Równanie stosowane w termodynamice chemicznej:

pν=ZRT (17)

gdzie: Z- współczynnik ściśliwości lub sprężystości , który urealnia równanie stanu gazu doskonałego:

(18)

B(T), C(T), D(T), ..- współczynniki wirialne (współczynniki indywidualne dla każdej substancji zależne od temperatury).

3.4. Mieszaniny gazów doskonałych i prawo Daltona.

Substancja czysta-jest to substancja składająca się z jednakowych cząstek.

Roztwór (mieszanina)- jest to substancja składająca się z kilku czystych substancji. Na przykład powietrze będące mieszaniną azotu, tlenu i innych substancji.

3.4.1. Skład mieszaniny

Mieszanina (roztwór) jest układem wieloskładnikowym, w którym każdy składnik rozmieszczony jest równomiernie w całej objętości.

Rozpatrujemy mieszaniny gazów doskonałych znajdujących się w równowadze termodynamicznej i nie reagujące między sobą chemicznie.

Skład mieszaniny określa się za pomocą udziałów składników. Udziały mogą być:

Udział masowy- jest to stosunek ilości składnika określonej za pomocą masy, do ilości m całej masy mieszaniny:

(19)

Ponieważ ∑ m_i=m ,zatem

(20)

Udział molowy-stosunek liczby kilomoli składnika n_i do liczby kilomoli całego roztworu:

(21)

i
(22)

Udział objętościowy-jest to stosunek objętości składnika V_i do objętości całego roztworu (mieszaniny) V, przy tym samym ciśnieniu i temperaturze:

; (23)

(24)

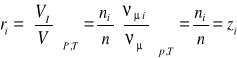
(25)

Związek ten jest prawdziwy ponieważ zgodnie z prawem Avogadra, przy jednakowych ciśnieniach i temperaturze objętości molowe składnika i roztworu (mieszaniny) są sobie równe tj. ν_μi=ν_μ.

Wielkość składnikowa -jest to wielkość określona dla składnika rozmieszczonego w całej objętości przy tej samej temperaturze T.

Wielkościami tymi mogą być:

• gęstość mieszaniny (roztworu):

(26)

• stężenie roztworu:

(27)

• objętościowe stężenie kilomolowe składnika C_i-jest to stosunek liczby kilomoli składnika do objętości

(28)

Ciśnienie udziałowe (składnikowe lub parcjalne)-jest to ciśnienie jakie wywierałby składnik gdyby sam tylko zajmował całą objętość V przy tej samej temperaturze T, jaką posiada mieszanina (roztwór):

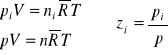
(29)

(30)

Prawo Daltona- suma ciśnień udziałowych wszystkich składników mieszaniny (roztworu) gazów doskonałych jest równa ciśnieniu mieszaniny.

Stała gazowa mieszaniny:

;

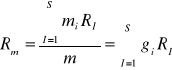
Ponieważ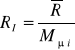
, to

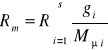
(31)

gdzie:M_μi-masa molowa i-tego składnika.

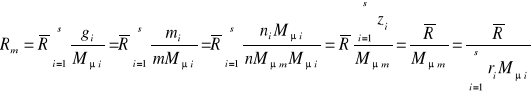
(32)

gdzie :M_μm- masa molowa mieszaniny

Zamiana udziałów masowych na udziały molowe:

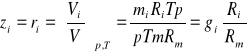
(33)

Zamiana udziałów molowych na udziały masowe:

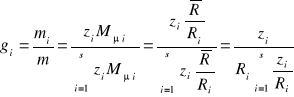
(34)

ponieważ
;

W praktyce często należy obliczyć gęstość mieszaniny (roztworu) gazów doskonałych mając gęstość składników przy tych samych ciśnieniach i temperaturach:

(35)

4.CIEPŁO WŁAŚCIWE GAZÓW

Ciepłem właściwym ciała nzw . ilość ciepła koniecznego do jego ogrzania o 1 stopień.

Ciepło właściwe m kg danej substancji definiuje się jako pochodną ciepła wymienionego podczas przemiany względem temperatury tej przemiany.

Ciepło właściwe ciała jest wielkością ekstensywną , ponieważ zależy od jego masy.

,

hyyugtygftufrcd

Rys.6. Interpretacja graficzna zależności doprowadzonego ciepła od temperatury
, ze względu na to ,że
stałej ,wykresem przemiany nie jest linia prosta.

Rzeczywiste ciepło właściwe interpretowane jest jako wartość tangensów kąta pochylenia stycznych przechodzących przez punkty 1 i 2 do osi odciętych T.

Ciepło właściwe obliczone przy skończonym przyroście temperatury nzw. Średnim ciepłem właściwym .

Na rys.6. odpowiada mu wartość tg
, tj. kąta jaki tworzy sieczna 1-2 z osią T.

Średnie ciepło właściwe przemiany
odniesione do 1kg jest:

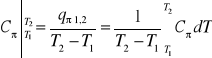
(37)

lub

(38)

Wartość średniego ciepła właściwego zależy od rodzaju przemiany termodynamicznej tzn. od sposobu wymiany ciepła .

W termodynamice często występuje ciepło właściwe przy stałym ciśnieniu C_p oraz ciepło właściwe przy stałej objętości C_v.

Wykładnik izentropy jest to stosunek wartości C_p do C_v:

---