Wyznaczanie stosunku ładunku elektronu do jego masy - e/m

Sekcja VII:

Mariusz Konsek

Marcin Kujawa

Marcin Sikora

Wstęp teoretyczny

Celem ćwiczenia jest wyznaczenie stosunku ładunku elektronu do jego masy. Do jego wyznaczenia wykorzystamy zjawisko odchylania poruszającego sie elektronu w polu magnetycznym. Zaczniemy od obliczenia prędkości z jaką porusza się elektron. Wyznaczymy ją z zależności, że energia kinetyczna poruszającego się elektronu jest równa pracy jaką musi wykonać nad nim pole elektrostatyczne, w którym porusza się elektron.

czyli stąd:

.

gdzie:

m - masa elektronu

e - ładunek elektronu

U - napięcie wytwarzające pole elektrostatyczne

v - prędkość poruszającego się elektronu.

Jeżeli teraz poruszający się elektron wejdzie w obszar działania pola magnetycznego to zacznie na niego działać siła zwana siłą Lorentza

Jest ona prostopadła do wektorów prędkości v i indukcji pola magnetycznego B. Zatem wzór końcowy na siłę działającą na elektron to:

Pod wpływem tej siły elektron zaczyna się poruszać ruchem jednostajnie przyspieszonym w kierunku prostopadłym do wektora prędkości początkowej. W skutek czego po czasie t tor ruchu elektronu ulega odchyleniu:

S = a t2/2

gdzie:

a = F_L/m, t = l/U

l - droga, na jakiej elektron jest odchylany przez pole magnetyczne

Podstawiając wszystkie zależności otrzymujemy:

otrzymujemy w rezultacie wzór :

gdzie:

i - natężenie prądu płynącego w cewkach

n - ilość zwojów w pojedynczej cewce

R - promień cewek (równy odległości między nimi)

Zauważmy że jeżeli przyjmiemy napięcie jako stałe (U = const), to otrzymamy liniową zależność:

Zaś jeżeli przyjmiemy jako stały prąd (i = const), to otrzymamy zależność :

Dzięki temu możemy w końcu obliczyć stosunek e do m:

.

Stanowisko pomiarowe i przebieg doświadczenia

W doświadczeniu wykorzystano następujące przyrządy:

- zasilacz prądu stałego zasilający cewki wytwarzające pole magntyczne,

- przełącznik do zmiany kierunku płynącego prądu,

- lampę oscyloskopową użytą do przyspieszania elektronów i do odczytu ich odchylania od pierwotnego toru ruchu,

- woltomierz służący do pomiaru napięcia przyspieszającego.

Podczas doświadczenia mierzyliśmy odległość pomiędzy położeniami plamki odchylonej przez pole o tej samej wartości ale przeciwnym zwrocie, dzięki czemu nie powstawał błąd spowodowany przez konieczność określenia dokładnego położenia plamki dla zerowej wartości natężenia pola odchylającego. Zmierzona w ten sposób wartość jest podwojoną wartością odchylenia.

Wykonując doświadczenie mierzyliśmy podwojone odchylenie dla ustalonego napięcia przyspieszającego przy zmiennym natężeniu prądu płynącego przez cewki Helmholtza.

Wykresy

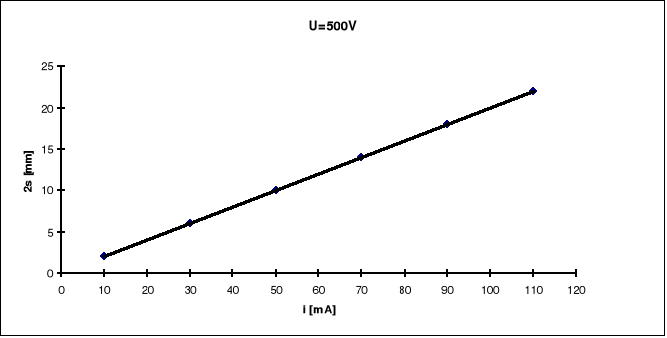
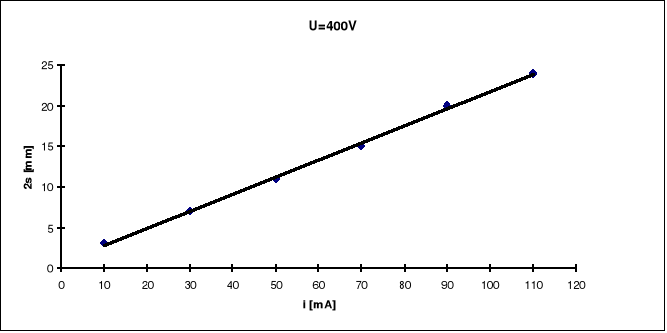
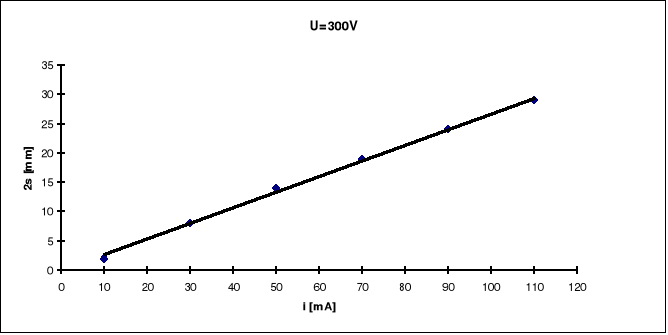
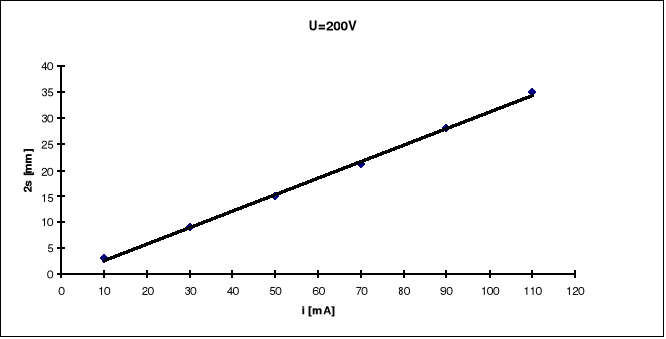
Opracowanie wyników

Poniższa tabela przedstawia wyniki obliczeń dokonanych na podstawie wzorów z instrukcji do ćwiczenia. Każdy z otrzymanych pomiarów odchylenia wiązki został oczywiście podzielony przez 2 przed przystąpieniem do dalszych obliczeń.

Nap. przysp	500 [V]	400 [V]	300 [V]	200 [V]
a[m*(C/kg*V)^1/2]	0.10025	0.1158	0.1408	0.1662
Δa[m*(C/kg*V)^1/2]	0.00077	0.0017	0.0017	0.0025
b [c m]	-0.0068	-0.012	-0.039	-0.054
Δb [c m]	0.0085	0.019	0.019	0.022
e/m [10^12 C/kg]	0.1452	0.155	0.1719	0.1597
(Δe/m)/(e/m) [1]	0.70	0.72	0.73	0.76
Δe/m [10^12 C/kg]	0.102	0.112	0.126	0.122
Wynik [10^12 C/kg]	0.15 + 0.11	0.16 + 0.12	0.17 + 0.13	0.16 + 0.13

Średnia ważona z 4 powyższych wyników wynosi:

,

.

Po zaogrągleniu wyniku otrzymujemy:

.

Wynik został przedstawiony w sposób najwygodniejszy do porównania z wartościami tablicowymi.

Porównując z wartościami tablicowymi:

e=1.602*10^-19 [C],

m_e=9.109*10^-31 [Kg],

.

Wnioski

Porównując wartości średniej ważonej i wartości tablicowej widzimy, że uzyskany wynik z błędem jest zbliżony do wartości tablicowej. Zwiekszenie dokładności pomiarów byłoby możliwe poprzez lepsze zogniskowanie plamki, a co za tym idzie zwiększenie dokładności odczytu odchylenia. Lepszy efekt dałoby też dokonywanie pomiarów tylko w centralnej części lampy oscyloskopowej aby uniknąć błędów związanych ze zniekształceniami powstającymi na jej obrzeżach.

---