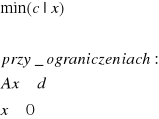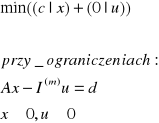egzamin z Metody Optymalizacji

M. Chudy

28.06.2006

egzamin składał się z 2 części:

• 4 zadania praktyczne (przynajmniej tak to Chudy okreścił ) , można korzystać z materiałów - 90minut

• 4 pytania z teorii, nie można korzystać z materiałów - 10 minut

ZAD 1 wysoko punktowane

Wykazać, że dane zadania PL są równoważne:

oraz

[chodziło mu chyba o coś z zadaniami prymalnymi/dualnymi, nikt na roku nie zrobił dobrze wg. Chudego]

ZAD 2 (identyczne jak zad2 z poprzedniego roku) wysoko punktowane, bardzo proste z książką

Zbadać, czy funkcja
jest zewnętrzną funkcją kary w zadaniu

[rozwiązanie prawie identycznego przykładu: książka Chudego str 115]

ZAD 3

podobne do zad3 z 2005 roku, z tym że rozwiązać algorytmem dualnym, funkcji i ograniczeń nie pamiętam

ZAD 4

Podobne do zad4 z 2005 roku, z tym że podać 2 różne zadania osłabione, funkcji i ograniczeń nie pamiętam

[(str 52) Chudy zapomniał wspomnieć, ze jak już się napisze te zadania osłabione, to należy udowodnić, że są to zadania osłabione do danego, więc należy to zrobić, nawet jak w poleceniu nie ma]

PYTANIE 1

Coś o warunkach optymalności rozwiązania w metodzie simplex

PYTANIE 2

warunki konieczne istnienia punktu siodłowego w metodzie Kuhna-Tuckera

[różniczkowalność funkcji (klasa C¹, wypukłość funkcji]

PYTANIE 3

Jakie są dopuszczalne kierunki dla punktu
ze względu na zbiór
?

[Definicja 7.4]

PYTANIE 4

Nie pamietam

---