2.a) Granica i ciągłość funkcji (odwzorowanie) F:Rn ⊃ Ux0 → Rk w punkcie x0. Definicje wg Cauchy'ego i wg Heinego.
Ciągłość:
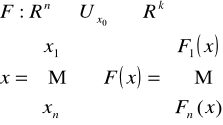
Mówimy, że funkcja
jest ciągła w punkcie x0∈DF, jeżeli:
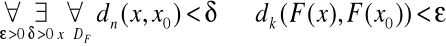
wg Cauchy'ego:
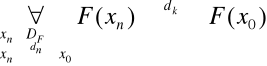
wg Heinego:
Granica:

Mówimy, że g jest granicą funkcji
![]()
w punkcie x0 ∈ Df i piszemy
jeżeli:
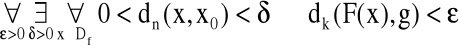
wg Cauchy'ego:
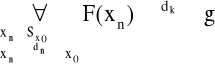
wg Heinego:
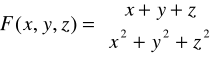
2.b) Zbadać ciągłość odwzorowania F:R3→R2,
w punkcie x0 = (0,0,0).
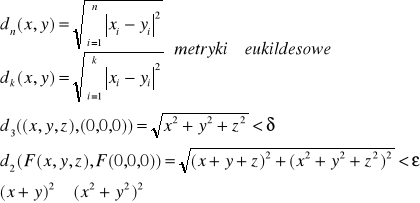
![]()
Z definicji Cauchy'ego:
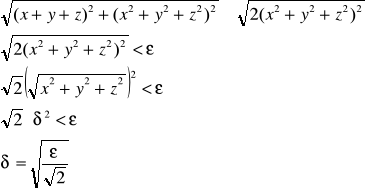
Odwzorowanie F:R3→R2 jest ciągłe.
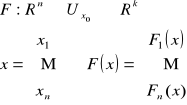
![]()
![]()
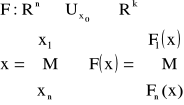
![]()
![]()
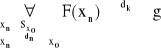
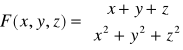
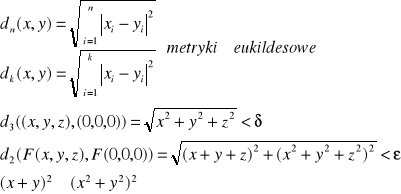
![]()
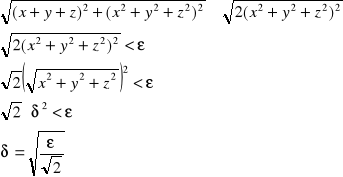
Wyszukiwarka
Podobne podstrony:
2001 06 02 matematyka finansowaid 21606
2008.06.02 matematyka finansowa
2001.06.02 matematyka finansowa
Matematyka I kolo, Studia PG, Semestr 02, Matematyka II, Kolokwia
2008 06 02 matematyka finansowaid 26453
2001 06 02 matematyka finansowaid 21606
02 Statystyka Matematyczna Zmienna Losowa Ciągłaid 3789
Logika matematyczna, ltm wyklad 02
Z Wykład 23.02.2008, Zajęcia, II semestr 2008, Analiza matematyczna
MATEMATYKA 02 11 a
I termin egzaminu z matematyki 02-02-2012 a
IMiR gzamin I z matematyki 03-02-2014
IMiR gzamin II z matematyki 10-02-2014
12 02 S1 W Matematyka
I termin egzaminu z matematyki 02-02-2012 b, Barbasze IMiR mibm
IMiR gzamin I z matematyki 01-02-2013
IMiR gzamin I z matematyki 01-02-2013
02-01-11 12 01 41 analiza matematyczna kolokwium 2002-01-16
więcej podobnych podstron