Nr ćwicz. 201	Data: 19.01 1995	Jacek Karaban	Wydział Elektryczny	Semestr III	Grupa I-2 godz.8^00-9^45
prowadzący mgr K.Łapsa					Przygotowanie:	Wykonanie:	Ocena ostat. :

Temat : Wyznaczanie zależności przewodnictwa od temperatury dla

półprzewodników i przewodników .

Wstęp teoretyczny

Prawo Ohma stwierdza , że :

,

gdzie j - gęstość prądu ,

E - natężenie pola elektrycznego ,

- przewodnictwo elektryczne .

Przewodnictwo elektryczne określone jest wzorem :

n , p - koncentracje nośników ,

n , p - ruchliwość nośników .

Ponieważ koncentracja i ruchliwość zależą od temperatury i rodzaju materiału , więc przewodnictwo elektryczne także zależy od tych czynników .

O zależności temperaturowej przewodnictwa w metalach decyduje tylko zmniejszanie się ruchliwości wraz ze wzrostem temperatury ( koncentracja nośników - elektronów - jest bardzo duża i nie zależy od temperatury ) . Zależność temperaturową wyraża się poprzez opór (R1/ ) :

,

R0 - opór w temperaturze T0 ,

- średni współczynnik temperaturowy .

W półprzewodnikach decydujący wpływ na przewodnictwo ma koncentracja nośników. W przypadku półprzewodników samoistnych koncentracja elektronów i dziur jest taka sama i wynosi :

,

Eg - szerokość pasma zabronionego .

Natomiast w półprzewodnikach domieszkowych koncentracje określone są poprzez poziomy energetyczne (zależnie od typu półprzewodnika ) Ed - donorowy , Ea - akceptorowy , oraz poprzez temperaturę :

.

Uwzględniając powyższe równania otrzymujemy wzór na temperaturową zależność przewodnictwa dla półprzewodników :

,

Edom jest jedną z wielkości Ed lub Ea zależnie od typu półprzewodnika .

W odpowiednio niskich temperaturach można zaniedbać w powyższym wzorze pierwszy składnik , natomiast w wysokich temperaturach ( po nasyceniu poziomów domieszkowych ) można zaniedbać składnik drugi . Odpowiednio dla tych dwóch przypadków wzór przyjmie postać :

.

Logarytmując jeden z powyższych wzorów otrzymamy zależność :

`

Z wykresu tej zależności wygodnie jest odczytać zależność przewodnictwa od temperatury :

Zasada pomiaru

Pomiarów oporu półprzewodnika i przewodnika dokonuje się w różnych temperaturach . Badane materiały umieszczone są w ultratermostacie , a ich opory mierzy się przy pomocy mostka Wheatstone'a .

Pomiary

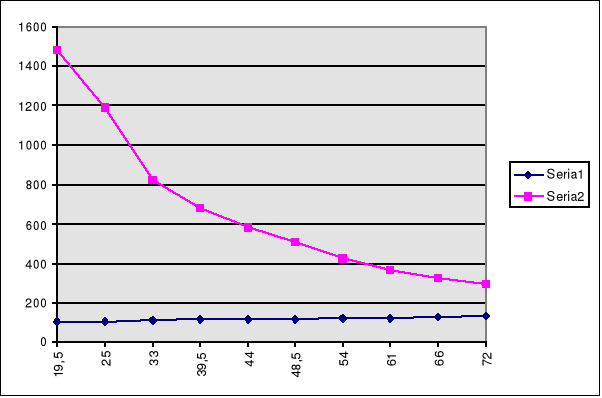
Przybliżone wartości oporów :

Rprz =200 Ω

Rpół =1200 Ω

Lp	T [K]	Rprz []	Rpółp []	1/t [1/C]	Δ(1/T) [1/C]	ln(1/R)	Δln(1/R)
1	19.5	105.6	1485	0,0513	0,0014	-7,303	0,00007
2	25	107.2	1190	0,0400	0,0008	-7,082	0,00009
3	33	110.3	823	0,0303	0,0005	-6,713	0,00013
4	39.5	113.3	680	0,0253	0,0004	-6,522	0,00015
5	44	115.2	582.2	0,0227	0,0003	-6,367	0,00018
6	48.5	116.9	510	0,0206	0,0003	-6,234	0,00020
7	54	119.1	424	0,0185	0,0002	-6,05	0,00024
8	61	123.0	366	0,0164	0,0002	-5,903	0,00028
9	66	125.0	324	0,0152	0,0002	-5,781	0,00031
10	72	130.6	293	0,0139	0,0001	-5,68	0,00035
11	77.5	123.7	263.9	0,0129	0,0001	-5,576	0,00038
12	83	128.1	245.1	0,0120	0,0001	-5,502	0,00041
13	92	132.3	214.5	0,0109	0,0001	-5,373	0,00047

Analiza pomiarów

Błąd pomiaru rezystancji mostkiem Wheatstone'a : R=0.1

Błąd pomiaru temperatury : T=0.5C

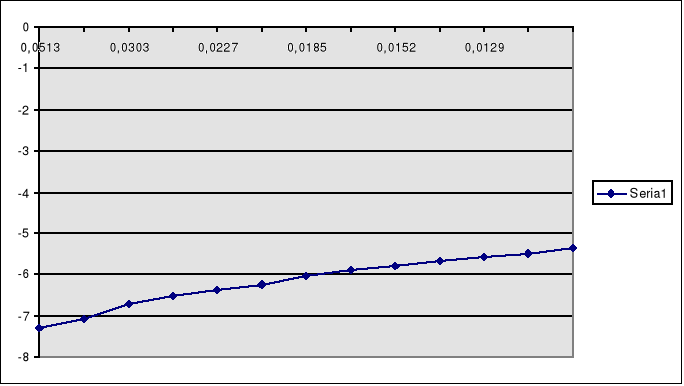
Współczynnik nachylenia prostej ln(1/R)=f(1/T) obliczony metodą regresji wynosi :

a= -43,94

a= ±0.01

Poziom domieszkowy będzie zatem równy :

Błąd wyznaczenia poziomu domieszkowego :

Wykresy:

Wykres zależności R=f(T)

Seria 1- półprzewodnik.

Seria 2 - przewodnik.

Wykres zależniści ln(1/R)=f(1/T)

Wynik końcowy:

E=(0.0007580.000002)eV

Wnioski:

---