Środek sił równoległych

Punkt C mający tę własność, że przechodzi przez niego stale wypadkowa danego układu sił równoległych od kierunku tych sił

(przy niezmiennych punktach przyłożenia i wartości sił) nazywa się

środkiem sił równoległych.

Wyprowadzenie wzorów określających współrzędne środka

sił równoległych.

Współrzędne punktu C obliczamy opierając się na twierdzeniu o momencie wypadkowej układu sił, według którego moment wypadkowej R względem dowolnej osi równy jest sumie momentów poszczególnych sił względem tejże osi.

Na rysunku 2 przedstawiony jest układ sił równoległych do osi z i tenże sam układ obrócony o kąt 90⁰. Wartość momentu względem osi y wypadkowej R przyłożonej do punktu C równa jest M_y = − R*x_C przy czym R = * P_i

Wartość momentu siły P_i przyłożonej w punkcie A_i wynosi M_iy = *P_i x_i

Z twierdzenia o momencie wypadkowej mamy

R x_C = * P_i x_ia

stąd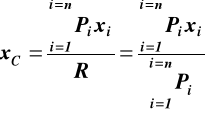

W podobny sposób przyrównując momenty względem osi x otrzymujemy

(to co wyżej, zamiast x podstawiamy y)

Obróćmy teraz wszystkie siły tak, aby stały się równoległe do osi x, nie zmieniając przy tym ich punktów przyłożenia

Porównując sumę momentów wszystkich sił względem osi y do odpowiedniego momentu wypadkowej przyłożonej do punktu C otrzymujemy trzecią współrzędną środka sił równoległych

(to co wyżej, zamiast y podstawiamy z)

Czym się różni środek sił równoległych od środka ciężkości?

Najczęściej spotykanym przykładem sił równoległych są siły ciężkości, tj. siły przyciągania cząstek ciała materialnego przez kulę ziemską. Siły te Możemy traktować jako równoległe, gdyż wymiary ciał rozpatrywanych w zastosowaniach technicznych zawsze są znikomo małe w porównaniu z promieniem kuli ziemskiej. Siły ciężkości działają na każdy element objętości danego ciała. W przypadku, gdy ciało ulega przemieszczeniu w przestrzeni, siły ciężkości zmieniają swój kierunek w stosunku do układu współrzędnych związanego z ciałem, jednakże punkty ich przyłożenia w stosunku do tego układu pozostają niezmienione.

Momentem bezwładności Jz figury płaskiej względem osi z nazywamy sumę iloczynów elementarnych pól dF tego pola przez kwadrat odległości tych pól od osi z.

Twierdzenie Steinera
Moment bezwładności dowolnego ciała względem dowolnej osi jest równy sumie momentu bezwładności względem osi centralnej oraz iloczynu pola F tej figury i kwadratu odległości obu osi: J_z=J_zc+Fa², gdzie
Jzc - moment bezwładności względem osi przechodzącej przez środek masy

Jz- moment bezwładności względem osi równoległej do pierwszej osi,

a- odległość między osiami,

F- pole bryły.

Oś centralna

Każda oś przechodząca przez środek ciężkości danego przekroju (danej figury płaskiej).

Biegunowy moment bezwładności - jest sumą osiowych momentów  bezwładności względem dwóch prostopadłych osi przechodzących przez ten biegun.
Jo = ∫ρ²dF

^F
Wskaźnik wytrzymałości przekroju na zginanie - jest to iloraz momentu bezwładności tego przekroju względem osi obojętnej (przechodzącej przez środek ciężkości przekroju) przez odległość od tej osi najdalszego elementu, należącego do przekroju.

Wskaźnik wytrzymałości przekroju na skręcanie  jest to iloczyn biegunowego momentu bezwładności przez odległość najdalszego elementu przekroju od osi skręcania.
Biegunowy moment bezwładności stanowi sumę momentów bezwładności względem osi prostopadłych.

Środek sił równoległych

Punkt C mający tę własność, że przechodzi przez niego stale wypadkowa danego układu sił równoległych od kierunku tych sił

(przy niezmiennych punktach przyłożenia i wartości sił) nazywa się

środkiem sił równoległych.

Wyprowadzenie wzorów określających współrzędne środka

sił równoległych.

Współrzędne punktu C obliczamy opierając się na twierdzeniu o momencie wypadkowej układu sił, według którego moment wypadkowej R względem dowolnej osi równy jest sumie momentów poszczególnych sił względem tejże osi.

Na rysunku 2 przedstawiony jest układ sił równoległych do osi z i tenże sam układ obrócony o kąt 90⁰. Wartość momentu względem osi y wypadkowej R przyłożonej do punktu C równa jest M_y = − R*x_C przy czym R = * P_i

Wartość momentu siły P_i przyłożonej w punkcie A_i wynosi M_iy = *P_i x_i

Z twierdzenia o momencie wypadkowej mamy

R x_C = * P_i x_ia

stąd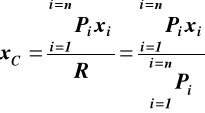

W podobny sposób przyrównując momenty względem osi x otrzymujemy

(to co wyżej, zamiast x podstawiamy y)

Obróćmy teraz wszystkie siły tak, aby stały się równoległe do osi x, nie zmieniając przy tym ich punktów przyłożenia

Porównując sumę momentów wszystkich sił względem osi y do odpowiedniego momentu wypadkowej przyłożonej do punktu C otrzymujemy trzecią współrzędną środka sił równoległych

(to co wyżej, zamiast y podstawiamy z)

Czym się różni środek sił równoległych od środka ciężkości?

Najczęściej spotykanym przykładem sił równoległych są siły ciężkości, tj. siły przyciągania cząstek ciała materialnego przez kulę ziemską. Siły te Możemy traktować jako równoległe, gdyż wymiary ciał rozpatrywanych w zastosowaniach technicznych zawsze są znikomo małe w porównaniu z promieniem kuli ziemskiej. Siły ciężkości działają na każdy element objętości danego ciała. W przypadku, gdy ciało ulega przemieszczeniu w przestrzeni, siły ciężkości zmieniają swój kierunek w stosunku do układu współrzędnych związanego z ciałem, jednakże punkty ich przyłożenia w stosunku do tego układu pozostają niezmienione.

Momentem bezwładności Jz figury płaskiej względem osi z nazywamy sumę iloczynów elementarnych pól dF tego pola przez kwadrat odległości tych pól od osi z.

Twierdzenie Steinera
Moment bezwładności dowolnego ciała względem dowolnej osi jest równy sumie momentu bezwładności względem osi centralnej oraz iloczynu pola F tej figury i kwadratu odległości obu osi: J_z=J_zc+Fa², gdzie
Jzc - moment bezwładności względem osi przechodzącej przez środek masy

Jz- moment bezwładności względem osi równoległej do pierwszej osi,

a- odległość między osiami,

F- pole bryły.

Oś centralna

Każda oś przechodząca przez środek ciężkości danego przekroju (danej figury płaskiej).

Biegunowy moment bezwładności - jest sumą osiowych momentów  bezwładności względem dwóch prostopadłych osi przechodzących przez ten biegun.
Jo = ∫ρ²dF

^F
Wskaźnik wytrzymałości przekroju na zginanie - jest to iloraz momentu bezwładności tego przekroju względem osi obojętnej (przechodzącej przez środek ciężkości przekroju) przez odległość od tej osi najdalszego elementu należącego do przekroju

Wskaźnik wytrzymałości przekroju na skręcanie  jest to iloczyn biegunowego momentu bezwładności przez odległość najdalszego elementu przekroju od osi skręcania.
Biegunowy moment bezwładności stanowi sumę momentów bezwładności względem osi prostopadłych.

Środek sił równoległych

Punkt C mający tę własność, że przechodzi przez niego stale wypadkowa danego układu sił równoległych od kierunku tych sił

(przy niezmiennych punktach przyłożenia i wartości sił) nazywa się środkiem sił równoległych.

Wyprowadzenie wzorów określających współrzędne środka

sił równoległych.

Współrzędne punktu C obliczamy opierając się na twierdzeniu o momencie wypadkowej układu sił, według którego moment wypadkowej R względem dowolnej osi równy jest sumie momentów poszczególnych sił względem tejże osi.

Na rysunku 2 przedstawiony jest układ sił równoległych do osi z i tenże sam układ obrócony o kąt 90⁰. Wartość momentu względem osi y wypadkowej R przyłożonej do punktu C równa jest M_y = − R*x_C przy czym R = * P_i

Wartość momentu siły P_i przyłożonej w punkcie A_i wynosi M_iy = *P_i x_i

Z twierdzenia o momencie wypadkowej mamy

R x_C = * P_i x_ia

stąd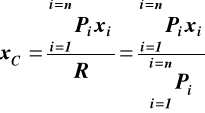

W podobny sposób przyrównując momenty względem osi x otrzymujemy

(to co wyżej, zamiast x podstawiamy y)

Obróćmy teraz wszystkie siły tak, aby stały się równoległe do osi x, nie zmieniając przy tym ich punktów przyłożenia

Porównując sumę momentów wszystkich sił względem osi y do odpowiedniego momentu wypadkowej przyłożonej do punktu C otrzymujemy trzecią współrzędną środka sił równoległych

(to co wyżej, zamiast y podstawiamy z)

Czym się różni środek sił równoległych od środka ciężkości?

Najczęściej spotykanym przykładem sił równoległych są siły ciężkości, tj. siły przyciągania cząstek ciała materialnego przez kulę ziemską. Siły te Możemy traktować jako równoległe, gdyż wymiary ciał rozpatrywanych w zastosowaniach technicznych zawsze są znikomo małe w porównaniu z promieniem kuli ziemskiej. Siły ciężkości działają na każdy element objętości danego ciała. W przypadku, gdy ciało ulega przemieszczeniu w przestrzeni, siły ciężkości zmieniają swój kierunek w stosunku do układu współrzędnych związanego z ciałem, jednakże punkty ich przyłożenia w stosunku do tego układu pozostają niezmienione.

Momentem bezwładności Jz figury płaskiej względem osi z nazywamy sumę iloczynów elementarnych pól dF tego pola przez kwadrat odległości tych pól od osi z.

Twierdzenie Steinera
Moment bezwładności dowolnego ciała względem dowolnej osi jest równy sumie momentu bezwładności względem osi centralnej oraz iloczynu pola F tej figury i kwadratu odległości obu osi: J_z=J_zc+Fa², gdzie
Jzc - moment bezwładności względem osi przechodzącej przez środek masy

Jz- moment bezwładności względem osi równoległej do pierwszej osi,

a- odległość między osiami,

F- pole bryły.

Oś centralna

Każda oś przechodząca przez środek ciężkości danego przekroju (danej figury płaskiej).

Biegunowy moment bezwładności - jest sumą osiowych momentów  bezwładności względem dwóch prostopadłych osi przechodzących przez ten biegun.
Jo = ∫ρ²dF

^F
Wskaźnik wytrzymałości przekroju na zginanie - jest to iloraz momentu bezwładności tego przekroju względem osi obojętnej (przechodzącej przez środek ciężkości przekroju) przez odległość od tej osi najdalszego elementu, należącego do przekroju.

Wskaźnik wytrzymałości przekroju na skręcanie  jest to iloczyn biegunowego momentu bezwładności przez odległość najdalszego elementu przekroju od osi skręcania.
Biegunowy moment bezwładności stanowi sumę momentów bezwładności względem osi prostopadłych.

---