Szkoła Główna Służby Pożarniczej
KATEDRA TECHNIKI POŻARNICZEJ		LABORATORIUM HYDROMECHANIKI
Ćwiczenie nr: 2 Temat: Określenie wydatku za pomocą pomiaru rozkładu prędkości dla przepływu osiowo symetrycznego.	Pluton: 3	Imię i nazwisko: Marek Kocielski
				Grupa: A
Prowadzący: bryg. mgr inż. Wojciech Zegar	Data wykon: 17.02.2003	Data złoż. .03.2002	Ocena:

1. CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie wydatku objętościowego przy pomocy pomiaru rozkładu prędkości stosując rurkę Prandtla.

2. STANOWISKO POMIAROWE

Stanowisko składa się z pomiarowej rury poziomej, pionowej rury z kryzą. Przepływ powietrza jest wymuszony wentylatorem odśrodkowym, napędzanym silnikiem elektrycznym. Regulację wydatku uzyskuje się poprzez zmianę położenia regulatora wydatku.

Ciśnienie dynamiczne jest mierzone rurką Prandtla, która jest przesuwana w płaszczyźnie prostopadłej do kierunku przepływu. Do kontroli ustawienia rurki pomiarowej względem ścianki rury służy odpowiednia podziałka.

Mikromanometr jest połączony różnicowo z rurką Prandtla. Ciśnienie różnicowe na kryzie jest wskazywane przez drugi mikromanometr.

3. WYKONANIE ĆWICZENIA

• Poziomujemy i zerujemy mikromanometry.

• Ustawiamy wydatek na regulatorze wydatku.

• Dokonujemy pomiaru rozkładu ciśnienia dynamicznego wzdłuż średnicy w punktach oddalonych od siebie o 3 mm.

• Notujemy położenie rurki Prandtla (promienia) i wskazania mikromanometra.

• Zapisujemy ustawienia mikromanometru.

• Notujemy wskazania spadku ciśnienia na kryzie.

4.TABELA POMIARÓW I WYNIKÓW OBLICZEŃ

Część pomiarowa				Część obliczeniowa
Lp.	R [mm]	L [mm]	L [mm]	Pd [Pa]	Vpow (R) [m/s]	R∙ V (R) [m^2/s]
1.	4	81	71	24,79	6,17	24,68
2.	7	90	71	27,55	6,51	45,57
3.	10	95	71	29,08	6,69	66,9
4.	13	98	71	29,99	6,79	88,27
5.	16	96	71	29,38	6,72	107,52
6.	19	98	71	29,99	6,69	127,11
7.	22	98	71	29,99	6,69	147,18
8.	25	101	71	30,91	6,89	172,25
9.	28	112	71	34,28	7,26	203,28
10.	31	126	71	38,56	7,7	238,7
11.	34	130	71	39,79	7,83	266,22
12.	37	134	71	41,01	7,94	293,78
13.	40	135	72	41,32	8,0	320
14.	43	136	71	41,62	8,0	344
15.	46	137	71	41,93	8,03	369,38
16..	48	137	71	41,32	8,0	384

5 PRZYKŁADOWE OBLICZENIA

Dane do obliczeń:

sin α _prandtla =

sin α _kryzy =

średnica rurociągu - d_r = 0,096 m ;

średnica kryzy - d_k = 0,0756 m ;

moduł kryzy - m=0,62 , F₂=0,0045 m².

ρ_pow=1,3
; ρ_cm = 780
; g=9,81

Wartość ciśnienia dynamicznego

p_d=ρ_cm⋅g⋅l⋅sinα=780⋅9,81⋅0,090⋅1/25=7651⋅0,090⋅0,04=27,54

Prędkość powietrza w punkcie pomiarowym

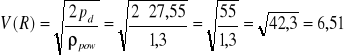
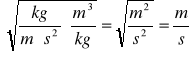
R⋅V_pow(R)

R= 7 [mm] = 0,007[m]

R₄⋅V =0,007⋅6,51=0,045

Wykres rozkładu prędkości f(R)=R*V(R) (w załączniku)

-Obliczenie pola trójkąta pod wykresem w granicy 0-R=48[mm]

a=4,8 [cm]

h=7,68 [cm]

F = ½ ∙ 4,8[cm] ∙ 7,68 [cm] = 18,43 [cm²]

Obliczenie wydatku objętościowego rzeczywistego:

Q_rz = 2π ∙ F ∙ κ

κ=x*y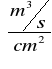

x→1cm = 0,01[m]

y→1cm = 0,05 [m²/s]

Q_rz=
=0,0579


=

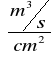
-Średnie wychylenie cieczy w mikromanometrze kryzy:

L_śr=

n_i - liczba pomiarów = 3

(liczba pomiarów na kryzie ograniczyliśmy do 3, ponieważ nie zanotowano dużych odchyleń od pomiaru pierwszego, stosunek zliczeń różnych od siebie wynosi ok. 1/3, czyli 1 pomiar = 0,072 na 2 pomiary 0,071)

L_śr=
=
[m]

h=L_śr⋅sinα=0,071⋅0,1=0,0071 m

• Obliczenie ciśnienia różnicowego na kryzie:

p_k = L_śr ∙ sin α _kryzy ∙ ρ_ciecz ∙ g [Pa]

sin α _kryzy = 0,1

L_śr = 71 [mm] = 0,071 [m]

p_k = 0,071 ∙ 0,1 ∙ 780 ∙ 9,81 = 54,3 [Pa]

• Obliczenie modułu kryzy

m = (dk/dr)²

dk - średnica kryzy

dr - średnica rury

m = (0,0756m/ 0,096m)² = 0,620

• Obliczenie wydatku zmierzonego kryzą:

F₂=
; p_k=

Q_t=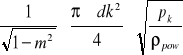
,

Q_t=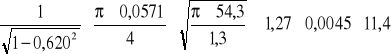
,

Q_t=0,065 [m³/s]

*******************

Drugi motyw:

=0,0045•1,27•28,91=0,165 ----- jeśli ten wzór to różnica miedzy wydatkami jest tak wielka ze nie wiem co mogło by być tego powodem

Współczynnik wydatku dla kryzy wynosi:

WNIOSKI

Wydatek teoretyczny kryzy obliczony w ćwiczeniu jest większy od wydatku rzeczywistego a spowodowane jest to nie uwzględnieniem w naszych obliczeniach strat ciśnienia na kryzie, oraz tym iż założyliśmy równomierny rozkład prędkości przepływu w przekroju rurociągu.

5

---