Tarnowska Milena Gr. 5

Obliczenia statyczno- wytrzymałościowe

1. Fundamenty

1. Założenia:

Do obliczeń statycznych fundamentów przyjęto nośność gruntu q_fn=0,15 MPa

a) Obciążenie osiowe przenoszone przez ławę:

- obciążenie pochodzące od ściany: N_oc = 77,73 kN/m

- obciążenie pochodzące od dachu: N_da= 6,39 kN/m

- obciążenie pochodzące od stropu: N_s = 33,15 kN/m

- obciążenie własne fundamentu: N_f = 5 kN/m

Obciążenie osiowe przenoszone przez ławę wynosi więc:

N_r = N_oc + N_s + N_da +N_f =122,27 kN/m

b) Grubość ściany konstrukcyjnej: 25 cm

c) Głębokość posadowienia ławy: 1,2 m

d) ława betonowa będzie wykonana z betonu klasy B15 i ze stali klasy A-III

e) Charakterystyczna wartość ciężaru objętościowego żelbetu: γ_z⁽ⁿ⁾ = 25 kN/m³

f) Wartość obliczeniowa ciężaru objętościowego gruntu: γ_gr⁽ⁿ⁾ = 17,5 kN/m³

2. Średnia obliczeniowa wartość obciążenia jednostkowego podłoża:

Średnia wartość obliczeniowa ciężaru ławy oraz gruntu spoczywającego na niej obliczona jako średnia arytmetyczna ciężarów obliczeniowych ławy i ziemi:

γ_śr^(r) = 0,5 · (γ_m · γ_z⁽ⁿ⁾ + γ_m · γ_gr⁽ⁿ⁾) = 0,5 · (1,1 · 25 + 1,1 · 17,5) = 23,4 kN/m³

Wartość obliczeniowa ciężaru objętościowego stopy i gruntu na 1 m:

G_r = B · 1 · 23,4 = 23,4 · B kN/m

Więc

q_rs = (N_r + G_r)/ (1 · B) = (122,27 + 23,4 · B)/ (1 · B) = 122,27 /B + 23,4 kPa

3. Parametry geotechniczne podłoża:

q_f⁽ⁿ⁾ = N_D · D_min · ϱ_D⁽ⁿ⁾ · g + N_B · B · ϱ_B⁽ⁿ⁾ · g

Ciężar objętościowy gruntu:

ϱ⁽ⁿ⁾ = 1,75 t/m³

Przyjęto:

ϱ⁽ⁿ⁾ = ϱ_B⁽ⁿ⁾ = ϱ_D⁽ⁿ⁾

Dla piasku pylastego o wartości ID równej 0.5 została odczytana z normy wartość charakterystyczna ψ_u⁽ⁿ⁾=30,5°.

N_D = 19,51 ; N_B = 8,19

4. Wartość oporu jednostkowego gruntu:

q_f⁽ⁿ⁾ = 19,51 · 1 · 1,75 · 10 + 8,19 · B · 1,75 · 10 = 341,4 + B · 143,4 kPa

Wartość obliczeniowa:

q_f = q_f⁽ⁿ⁾ · γ_m = 0,75 · (341,4 + B · 143,4) = 207,4 + B · 87,1 kPa

5. Wyznaczenie szerokości ławy fundamentowej:

Dla q_rs = 122,27 /B + 23,4 kPa

207,4 + B · 87,1 kPa=122,27 /B + 23,4 kPa

=>szerokość ławy fundamentowej spełniającej warunki wytrzymałościowe wynosi B = 0,53m, więc przyjęta w projekcie wartość B = 0,7 m wytrzyma obciążenie.

6. Wymiarowanie ławy:

Obliczenie wartości momentu zginającego:

M = (N_r · C²)/ (2 · B) = (122,27· 13²)/ (2 · 0,5) = 20,66 kNm

Wysokość ławy fundamentowej:

h > 2,7 ·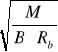
= 2,7 ·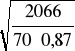
= 15,72 cm

Przyjęto wysokość ławy h=30 cm, w tym 5 cm otuliny, stąd h₀=25 cm, co jest wartością większą od wyliczonej minimalnej wysokości ławy fundamentowej.

Sprawdzenie ławy na przebicie:

q_r = N_r/ 1 · B = 122,27/ 0,7 = 174,67 kN/m²

P = N_r - q_r · (a + 2 · h₀) · 1 =122,27- 174,67 · (0,25 + 2 · 0,25) = -8,73 kN

R_ba · h₀ · u_p = 0,075 · 25 · 200 = 375 kN

P < R_ba · h₀ · u_p

7. Pole przekroju uzbrojenia:

F_a = M/ (0,9 · h₀ · R_a) = 2066 / (0,9 · 25 · 35) = 2,62 cm²

Przyjęto pręty zbrojeniowe θ=10 mm ułożone co 25 cm. Ich pole przekroju wynosi
F_a = 3,14 cm² co przekracza minimalną wartość F_a.

2. Ściany- sprawdzenie warunków wytrzymałościowych dla ściany nośnej

Założenia:

a) Całkowite obciążenie obliczeniowe działające na ścianę:

- ciężar własny stropu: Q_s = (0,24+0,96+2,1+3,17)kN/m²=6,47 kN/m²

Obciążenia:

• parkiet: g₁=0,24 kN/m²

• podkład cementowy (wylewka cementowa) g₂=0,96 kN/m²

• Obciążenie użytkowe g₃= 2,1 kN/m²

• Płyta żelbetowa g₄=3,17 kN/m²

-rozpiętość obliczeniowa stropu: z = 10,25 m

- obciążenie własne ściany- ściana wykonana z cegły pełnej o grubości 25 cm, tak powstały mur ma gęstość objętościową 1800 kg/m³+ tynk cementowo- wapniowy o grubości 1 cm+ styropian grubości 6 cm : 18 kN/m³·0,25 m·1m = N_śc = 4,5 kN/m+ tynk 0,01m+styropian 0,06m =(4,5+0,494+ 0,032) kN/m= 5,026 kN/m

- obciążenie przenoszone z dachu: (ciężar: dachówka 0,55kN/m²; konstrukcja drewniana 0,25 kN/m²) rozpiętość obliczeniowa dachu: 13,93 m ; N_da= 0,8 kN/m2·sin α·13,93m= 6,39 kN/m

α=35⁰ ; sin α= 0,5735;

Ściana obciążana jest przez strop na dwóch kondygnacjach:

Obciążenie działające na ścianę wynosi więc:

N_oc = 2 · (Q_s · (z/2)) + N_śc + N_da = 2· (6,47*10,25/2)+5,026+6,39=77,73 kN/m

b) Obciążenie występuje jedynie w płaszczyźnie pionowej, obciążenia poziome wynikające z parcia lub ssania wiatru pominięto.

c) Ściana konstrukcyjna ma grubość: 25 cm

d) Wysokość w świetle stropu: hs = 2,6 m

W celu sprawdzenia granicznej nośności ścian należy wykazać, że obliczeniowe obciążenie ściany nie przekracza dopuszczalnej nośności obliczeniowej:

N_oc < N_od

N_od = φ_m · A · f_d

Wartość częściowego współczynnika bezpieczeństwa γ_m = 1,7 - dla elementów murowych I kategorii i kategorii wykonania „A”.

Cecha sprężystości muru: α_c = 600

Wysokość efektywna ściany:

h_ef = h · ϱ_h · ϱ_n

ϱ_h = 1 dla ściany usztywnionej

ϱ_n = 1 dla modelu przegubowego

h_ef = 2,6 · 1 · 1 = 2,6 m

Smukłość ściany przy t = 0,3 m:

h_ef/ t = 2,6/ 0,3 = 8,666 co jest mniejsze od wartości granicznej równej 18

Mimośród przypadkowy:

e_a = h_ef/ 300 = 8,6666 mm = 0,008666 m

Zastępczy mimośród początkowy przyjęto jako równy mimośrodowi przypadkowemu

e_m = e_a = 0,008666 m

Współczynnik redukcyjny przy h_ef/ t = 8,6666 i α_c = 600 wg normy PN-B-03002:1999 wynosi:

φ_m = 0,83

Nośność ściany wyniesie więc:

f_k = 2,1 MPa

f_d = f_k/ γ_m = 2,1/ 1,7 = 1,235 MPa

N_od = φ_m · A · f_d = 0,83 · 10³ · 0,25 · 1 · 1,235 = 256,26 kN/m

77,73 kN/m <256,26 kN/m

Spełniony jest zatem warunek : N_oc < N_od

3. Obliczenia statyczne elementów więźby dachowej- sprawdzenie warunków wytrzymałościowych

Założenia:

1. Kąt nachylenia połaci dachu: α = 35^o (sinα = 0,573 ; cosα = 0,819)

2. Rozstaw krokwi: a = 0,75 m

3. Długość krokwi: 6,025 m

4. Budynek znajduje się w Krakowie: I strefa obciążenia wiatrem oraz II strefa obciążenia śniegiem

5. Charakterystyczne obciążenia własne od pokrycia dachu na 1 m² z uwzględnieniem łat, krokwi, deskowania, ocieplenia i dachówki bitumicznej przyjęto: g_k = 0,8 kN/m²

Obciążenia stałe:

Przyjęto średni współczynnik dla obciążenia stałego: γ_f = 1,2

Wartość obliczeniowa obciążenia stałego: g_d = 0,8 · 1,2 = 0,96 kN/m²

Obciążenia zmienne:

a) od wiatru

Obciążenie charakterystyczne wywołane działaniem wiatru:

P_k = q_k · C_e · C_z · ß

q_k = 0,25 kN/m² - charakterystyczne ciśnienie prędkości wiatru

C_e = 1,0 - współczynnik ekspozycji

β = 1,8 - współczynnik porywów wiatru

C=C_z = 0,015α-0,2=0,015· 40-0,2= 0,4 - współczynnik aerodynamiczny

P_k = 0,25 · 1,0 · 0,4 · 1,8 = 0,18 kN/m²

Obciążenie obliczeniowe:

P = P_k · γ_f

γ_f = 1,3

P = 0,18 · 1,3 = 0,23 kN/m²

0,18 kN/m² < 0,23 kN/m²

Spełniony jest warunek: P_k < P

b) od śniegu

Obciążenie charakterystyczne śniegiem dachu:

S_k = Q_k · C

Q_k = 0,9 kN/m² - obciążenie charakterystyczne śniegiem gruntu

C = 0,8 - współczynnik kształtu dachu

S_k = 0,9 · 0,8 = 0,72 kN/m²

Obciążenie obliczeniowe:

S_d = S_k · γ_f

γ_f = 1,4

S_d = 0,72 · 1,4 = 1,01 kN/m²

0,72 kN/m² < 1,01 kN/m²

Spełniony jest warunek: S_k < S_d

Obliczenia krokwi:

Przyjęto układ krokwi w postaci belki swobodnie podpartej w murłacie i płatwi. Rozpiętość obliczeniowa krokwi:

l_d = 3,66

Obciążenia stałe prostopadłe do połaci dachu:

obciążenia charakterystyczne:

q_k = a · g_k · cosα = 0,75 · 0,8 · 0,819 = 0,491 kN/m²

obciążenia obliczeniowe

q_d = a · g_d · cosα = 0,75 · 0,96 · 0,819 = 0,589 kN/m²

Obciążenia zmienne prostopadłe do połaci dachu:

obciążenia charakterystyczne:

p_k = a · (s_k · cos²α + w_k) = 0,75 · (0,72 · 0,819² + 0,18) = 0,497 kN/m²

obciążenia obliczeniowe:

p_d = a · (s_d · cos²α + w_d) = 0,75 · (1,01 · 0,819² + 0,23) = 0,68 kN/m²

Maksymalny obliczeniowy moment zginający:

M_y,d = 0,125 · (q_d + p_d) · l_d² = 0,125 · (0,589 +0,68) · 3660² = 2124877,05 N·mm

Wytrzymałości charakterystyczne materiału

na zginanie f_m,k = 35,0 N/mm²

na ściskanie wzdłuż włókien f_a,0,k = 25,0 N/mm²

na ścinanie f_v,k = 3,48 N/mm²

średni moduł sprężystości wzdłuż włókien E_0,mean = 13,0 kN/mm²

na ściskanie w poprzek włókien f_c,90,k = 6,0 N/mm²

Dla pierwszej klasy użytkowania i obciążeń krótkotrwałych współczynnik modyfikacyjny

k_mod = 0,9

Odpowiednie wytrzymałości obliczeniowe:

f_m,d = (f_m,k · k_mod)/ γ_M = (35 · 0,9)/1,3 = 24,23 N/mm²

f_a,0,d = (f_a,0,k · k_mod)/ γ_M = (25 · 0,9)/1,3 = 17,31 N/mm²

f_v,d = (f_v,k · k_mod)/ γ_M = (3,4 · 0,9)/1,3 = 2,35 N/mm²

Przyjęto krokwie o wymiarach przekroju 80x160 mm.

Wskaźnik wytrzymałości przekroju krokwi:

W_y = (b · h²)/6 = (80 · 160²)/6 = 341333,34 mm³

Moment bezwładności przekroju krokwi:

I_y = (b · h³)/12 = (80 · 160³)/12 = 27306666,67 mm⁴

Sprawdzenie warunku stanu granicznego nośności krokwi

σ_m,d = M_y,d / W_y,d = 2124877,05 / 341333,34 = 6,225 N/mm²

6,225 N/mm²< 24,23 N/mm²

Spełniony jest warunek: σ_m,d < f_m,d

Sprawdzenie warunku stanu granicznego użytkowalności krokwi

u_fin = (5 · l_d⁴ · [q_k · (1 + k_def,q) + p_k · (1 + k_def,p)] ) / (384 · E_0,mean · I_y) =

= (5 · 3660⁴ · [0,491 · (1 + 0,6) +0,497 · (1 + 0)] ) / (384 · 13000 ·27306666,67) = 8,441 mm

l_d/200 = 3660/200 = 18,3 mm

8,441 mm < 18,3 mm

Spełniony jest warunek: u_fin < l_d/200

Obliczenia płatwi:

Przyjęto, że obciążenie od krokwi jest rozłożone równomiernie. Na płatew działa obciążenie z pasa o szerokości:

0,5 · I_d + I_g = 0,5 · 3,66 + 2,71 = 4,54 m

Rozpiętość obliczeniowa płatwi w płaszczyźnie poziomej

I_z,d = 0,22 m

W płaszczyźnie pionowej płatew jest podparta w osiach słupów.

I_y,d = 1,73 m

Przyjęto płatew o wymiarach przekroju 160x160 mm.

Wskaźniki wytrzymałości przekroju płatwi:

W_y = W_z = (b · h²)/6 = (160 · 160²)/6 = 682666,67 mm³

Momenty bezwładności przekroju płatwi:

I_y = I_z = (b · h³)/12 = (160 · 160³)/12 = 54613333,33 mm⁴

Obciążenia pionowe stałe działające na płatew:

a. obciążenia charakterystyczne:

q_y,k = g_k · (0,5 · l_d + l_g) = 0,8 ·4,54 = 3,632 N/mm

b. obciążenia obliczeniowe:

q_y,d = g_d · (0,5 · l_d + l_g) = 0,96 · 4,54 = 4,358 N/mm

Obciążenia pionowe zmienne działające na płatew:

a. obciążenia charakterystyczne:

p_y,k = (s_k · cosα + w_k · cosα) · (0,5 · l_d + l_g) = (0,72 · 0,819+ 0,18 · 0,819) · 4,54 = 3,346 N/mm

b. obciążenia obliczeniowe

p_y,d = (s_d · cosα + w_d · cosα) · (0,5 · l_d + l_g) = (1,01 · 0,819 + 0,23 · 0,819) · 4,54 = 4,61 N/mm

Obliczenia poziome działające na płatew:

a. obciążenia charakterystyczne:

p_z,k = w_k · sinα · (0,5 · l_d + l_g) = 0,18 · 0,573 · 4,54 = 0,468 N/mm

b. obciążenia obliczeniowe

p_z,d = w_d · sinα · (0,5 · l_d + l_g) = 0,23 · 0,573 · 4,54 = 0,598 N/mm

Maksymalne obliczeniowe momenty zginające:

M_y,d = 0,125 · (q_y,d + p_y,d) · I_y,d² = 0,125 · (4,358 +4,61) · 1730² = 3355040,9 Nmm

M_z,d = 0,125 · p_z,d · I_z,d² = 0,125 · 0,598 · 220² = 3617,9 Nmm

Sprawdzenie warunku stanu granicznego nośności płatwi:

σ_y,m,d = M_y,d / W_y =3355040,9/682666,67 = 4,915 N/mm²

σ_z,m,d = M_z,d / W_z = 3617,9 / 682666,67 = 0,0052983 N/mm²

=4,915 N/mm²

4,915 N/mm² < 24,23 N/mm²

Spełniony jest warunek:
< f_m,d

Sprawdzenie warunku stanu granicznego użytkowalności płatwi:

u_y,fin = (5 · l_y,d⁴ · [q_y,k · (1 + k_def,q) + p_y,k · (1 + k_def,p)] ) / (384 · E_0,mean · I_y) =

= (5 · 1730⁴ · [3,632 · (1 + 0,6) +3,346 · (1 + 0)] ) / (384 · 13000 ·54613333,33) = 1,504 mm

u_z,fin = (5 · l_z,d⁴ · [p_z,k · (1 + k_def,w)] ) / (384 · E_0,mean · I_z) =

= (5 · 220⁴ · [0,468 · (1 + 0,6)] ) / (384 · 13000 · 54613333,33) = 3,217· 10^-5 mm

=1,504 mm

l_y,d/250 = 1730/250 = 6,92 mm

1,504 mm <6,92 mm

Spełniony jest warunek:
< l_y,d/250

Obliczenia słupa:

Słup jest ściskany siłą osiową:

N_c,d = (q_y,d + p_y,d) · I_y,d = (4,358 +4,61) · 1730 = 15514,64 N

Przyjęto słup długości 1,93 m i o wymiarach przekroju 80x80 mm.

Powierzchnia przekroju słupa:

A_d = 6400 mm²

Momenty bezwładności przekroju słupa:

I_z = I_y = (b · h³)/12 = (80 · 80³)/12 = 3413333,33 mm⁴

Promienie bezwładności przekroju słupa:

i_z = i_y =
=
= 23,09 mm

Smukłość słupa:

λ_y = λ_z = l_s/i_z = 1930/23,09 = 83,58

Naprężenie krytyczne przy ściskaniu:

σ_c,crit,y = (π² · E_0,05)/ λ_y² = (π² · 8000)/ 83,58² = 11,29 N/mm²

Smukłość sprawdzana przy ściskaniu:

λ_rel,y =
=
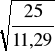
= 1,488

k_y = 0,5 · (1 + βc · (λ_rel,y - 0,5) + λ_rel,y²) = 0,5 · (1 + 0,2 · (1,488- 0,5) + 1,488²) = 1,705

Współczynnik wyboczeniowy:

k_c,y = 1/ (k_y +
= 1/ (1,705+
= 0,252

Sprawdzenie warunku stanu granicznego nośności słupa:

σ_c,0,d = N_c,d/ (k_c,y · A_d) = 15514,64 / (0,252 · 6400) = 9,619 N/mm²

9,619 N/mm² <17,31 N/mm²

Spełniony jest warunek: σ_c,0,d < f_a,0,d

Docisk słupa do podwaliny:

N_c,90,d = N_c,d = 15514,64 N

Wytrzymałość obliczeniowa drewna na docisk:

f_c,90,d = (f_c,90,k · k_mod)/ γ_M = (6 · 0,9)/ 1,3 = 4,15 N/mm²

Naprężenie docisku:

σ_c,90,d = N_c,90,d/ A_d =15514,64 /6400 = 2,424 N/mm²

2,424 N/mm²< 4,15 N/mm²

Spełniony jest warunek: σ_c,90,d < f_c,90,d

Obliczenia miecza:

Przyjęto miecze o wymiarach 70x70 mm.

Powierzchnia przekroju miecza:

A_d = 4900 mm²

Momenty bezwładności przekroju mieczy:

I_y = I_z = (b · h³)/12 = (70 · 70³)/12 = 2000833,33 mm⁴

Promienie bezwładności przekroju mieczy:

i_z = i_y =
=
= 20,2 mm

Miecze są nachylone pod kątem α=45° do płatwi w miejscu podparcia pierwszej krokwi.

Stąd długość miecza:

l_d = 800/ cos45° = 1131,37 mm

Siła pionowa przekazywana przez płatew na miecz:

V = 0,5 · (q_y,d + p_y,d) · l_y,d = 0,5 · (4,358 +4,61) · 1730 = 7757,32 N

Siła osiowa w mieczu:

N_c,d = V/ sin45° = 10970,5

Smukłość miecza:

λ_y = λ_z = l_d/i_z = 1131,37/20,2 = 56,01

Naprężenia krytyczne przy ściskaniu:

σ_c,crit,y = (π² · E_0,05)/ λ_y² = (π² · 8000)/ 83,58 ² = 11,29 N/mm²

Smukłość sprawdzana przy ściskaniu:

λ_rel,y =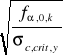
=
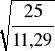
= 1,48

k_y = 0,5 · (1 + β_c · (λ_rel,y - 0,5) + λ_rel,y²) = 0,5 · (1 + 0,2 · (1,48- 0,5) + 1,48²) = 1,693

Współczynnik wyboczeniowy:

k_c,y = 1/ (k_y +
= 1/ (1,693+
= 0,253

Sprawdzenie warunku stanu granicznego nośności miecza:

σ_c,0,d = N_c,d/ (k_c,y · A_d) = 10970,5/ (0,253 · 4900) = 8,849 N/mm²

8,849 N/mm²< 17,31 N/mm²

Spełniony jest warunek: σ_c,0,d < f_a,0,d

---