Fizyka:

ad1). Dynamika punktu materialnego.

I zasada. Jeżeli na ciało nie dział żadna siła lub siły się równoważą to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

II zasada. Pod wpływem siły ciało porusza się ruchem prostoliniowym jednostajnym
,

III zasada.(zasada akcji i reakcji).

Jeżeli ciało A działa na ciało B siłą to ciało B działa siłą na ciało A tylko odwrotnie zwróconą.

Siła
może być funkcją położenia ciała, prędkości tego ciała i czasu.

Podstawowe zagadnienia w dynamice: znając siłę działającą na ciało określić ruch tego ciała. Znając siłę
oraz tzw. warunki początkowe (położenie ciała i prędkość w jakieś chwili czasu np. t=0) znaleźć ruch tego ciała czyli np.: odtworzyć prędkość i tor tego ciała:

ponieważ:

ad1)

rysunek w notatkach

-wektor wodzący

-

prędkość ruchu

a)prędkość średnia: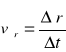

b)prędkość chwilowa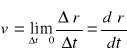

W układzie kartezjańskim

=[v_x,v_y,v_z]

v_x=
, v_y=
, v_z=

przyśpieszenie

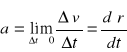
[a_x,a_y,a_z]

a_x=
, a_y=
, a_z=

a_x=
-druga pochodna

ad2)

Klasyfikacja ruchów ze względu na:

a)tor:prostoliniowe i krzywoliniowe

b)prędkość: jednostajne (v-const.) i zmienne

c)przyśpieszenie: jednostajnie zmienne (a-const), niejednostajnie zmienne

ad3)

a=const.

W chwili t=0 prędkość wynosi v₀

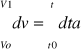
v_k-v₀=a
, v_k-v₀ =at
, v_k-v₀ =at-a0, v_k-v₀ =at, v_k=v₀ +at

droga:s=
,s=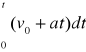
=
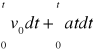
=v₀
+a
=v₀t+a

s=v₀t+a

ad4)

Przyśpieszenie styczne - opisuje zmianę wartości prędkości v.

Przyśpieszenie normalne(prostopadłe do tor). Opisuje zmianę kierunku wektora prędkości.

Ad6)

Rysunek w notatkach

Ruch po okręgu.

W czasie Δt, R zakreśla kątΔα

Δα=

prędkość kątowa

v=Rω

Ad9)

X=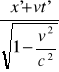
, y=y' ,z=z', t=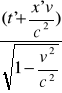

x'=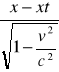
, y'=y , z'=z , t'=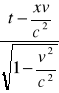

Ad10)

Konsekwencje transformacji Lorentza są następujące:

a)dylatacja czasu czyli czas w układzie poruszającym się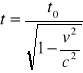
t₀-czas właściwy,mierzony w układzie spoczywającym t>t₀

b) skrócenie długości (skrócenie Fitzgeralda)

L₀ = x₂-x₁

L= L₀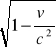
L>L₀ Jeżeli v<<c, to

0 i tr.L.
trans. Galieusza.

Ad16)

II zasada dynamiki

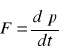
Jeżeli w chwili t=0 ciało posiada pręd.v₀

to po czasie t

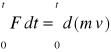
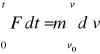
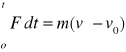
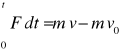
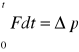
Lewa strona nazywa się popędem siły

POPĘD SIŁY = PRZYROSTOWI PĘDU CIAŁA.

Ad 18)

Zasada zachowania pędu z II zasady dynamiki N.

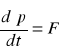
jeżeli
,to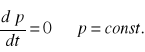

13.(Zas.Newtona).

1.Zas.Jeżeli na ciało nie działa żadna siła lub siły działające wzajemnie się równoważą to ciało jest w spoczynku lub porusza się ruchem jednostajnie prostoliniowym.(Ciało nie zmienia stanu ruchu).

2.Zas.Pod wpływem siły przyśpieszenie jest wprost proporcjonalne do siły ciała, a odwrotnie proporcjonalne do masy.

3.Zas.akcji i reakcji.

Jeżeli na ciało A działa ciało B to ciało B oddziaływuje na ciało A tylko przeciwnie zwrócone.
.Siła F może być funkcją
, gdzie

t-czas,v-prę.cziła,r-położenie ciała.

11.Dylatacja czasu.

Czas w ukł. poruszającym się: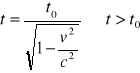
gdzie:

t₀-czas własny zdarzenia, t-czas mierzony w ukł.spoczywającym.

12.Skruceniu dł. Fitzgeralda podlegają tylko wymiary równoległe do osi x, natomiast y i z nie ulegają zmianie.

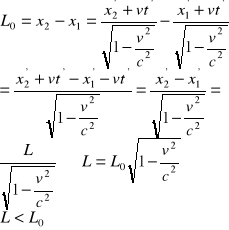
14.Oscylator.

k-stała sprężystości

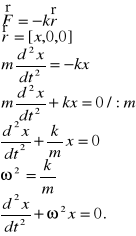
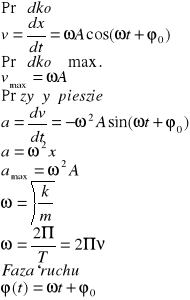
v=1/t-częstotliwość ruchu

19.Siła centralna. Kierunek działania jest wzdłuż prostej łączącej dwa ciała a wart. Zależy od odległości między ciałami.

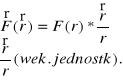
Przykłady sił cen.

a)siła spręrzystości(powoduje ruch harmoniczny).

b)siła grawitacji-prawo powszechnego ciążenia.

Każde dwie masy przyciągają się siłą wprost proporcjonalną do iloczynu masy, a odwrotnie proporcjonalnie do kwadratu odległości między tymi masami.

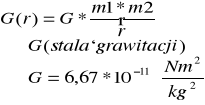
c)siła działająca między ładunkami elektrycznymi.

Prawo Coulomba-Każde dwa ładunki różno imienne przyciągają się a jedno imienne odpychają z siłą wprost proporcjonalną do iloczynu ładunku i odwrotnie proporcjonalnie do kwadratu odległości między nimi.

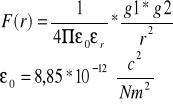
-przenikalność elektryczna próżni

-względna przenikalność elektryczna ośrodka w którym znajdują się ładunki

Wspólną cechą tych sił jest zal.

20.

Natężenie pola grawitacyjnego-nazywamy stosunek siły grawitacyjnej do wielkości masy:

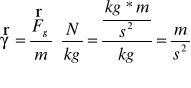
Dla pola grawitacyjnego pochodzącego od pojedyńczej masy M:

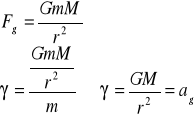
a_g-przyśpieszenie grawitacyjne

Dla pola grawitacyjnego ziemi, gdy r=Rz:

Energia potencjalna masy m w polu M:

Potencjał pola grawitacyjnego-stosunek energii potencjalnej punktu materialnego, umieszczonego w danym punkcie pola do masy:

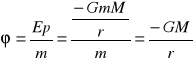
Natężeniem pola elektrostatycznego-naz. stosunek siły Fe do wielkości tego ładunku q:

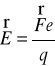
q-próbny ładunek dodatni

Z prawa Coulomba:

Gdzie:

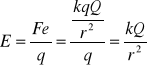
Q-żródło pola

Energia potencjalna w tym polu:

Potencjałem pola elektrostatycznego-naz. stosunek Ep do ładunku q:

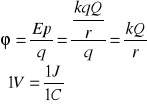
Różnica potencjałów nazywa się napięciem:

Ładunek elementarny:

7.Transf.Galileusza.

Względność ruchu polega na obserwacji obiektu P przez dwóch obserwatorów, jeden względem ukł.spoczywającego a drugi względem ukł.poruszającego się. Każdy ruch jest względny, gdyż wymaga ukł.odniesienia. Układ s'porusza się z prędk.
względem układu spoczywającego s.Ruch punktu P opisany jest w układzie s:

układzie s':

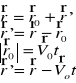
Wzory transf.Galileusza:

x'=x-Vxt

y'=y-vyt

z'=z-Vzt

t'=t

W szczególnym przypadku:

x'=x-Vxt

y'=y

z'=z

t'=t

Transf.Galilleusza-prędkość:

po zróżniczkowaniu:

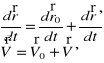
Pytanie 21.

Pole grawitacyjne i elektrostatyczne jest zachowawcze, tzn. że wartość pracy w polu grawitacyjnym i elektrostatycznym nie zależy od drogi, lecz jedynie od współrzędnych radialnej r początkowego i końcowego, między którymi została wykonana praca.

Praca w polu grawitacyjnym:

c=Gm₁m₂ W_AB= Gm₁m₂(1/r₁-1/r₂)

gdy r₂ > r₁ W_AB > 0

Praca w polu elektrostatycznym:

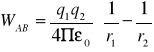
gdy r₂ > r₁ i q₁ i q₂ różnoimienne

W_AB > 0

Pytanie 22.

Energia potencjalna-odnosi się tylko do pól zachowawczych.

Energią potencjalną punktowej masy (ładunku) w polu grawitacyjnym (elektrostatycznym) - nazywamy pracę jaką muszą wykonać siły pola, aby przenieść ładunek (masę) z danego punktu do nieskończoności.

(*)Energia pot. w polu elektrostatycznym:

Energia pot. w polu grawitacyjnym:

Pytanie 23.

Związek między pracą, a energią potencjalną:

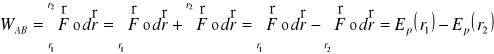
Związek między siłą, a energią potencjalną:

Z definicji pracy:

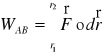
Ze związku między pracą , a energią potencjalną:

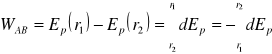
Porównując funkcje podcałkowe:

Pytanie 24.

Własności sił centralnych postaci F(r)=C/r²:

1.Praca przy przemieszczaniu ciała z pkt. A do pkt. B

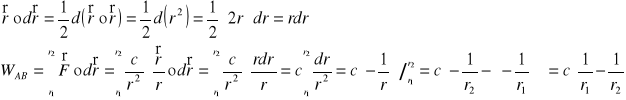
2. Energia potencjalna w polu siły F(r)=C/r² jest odwrotnie proporcjonalna do r (* wstaw wzory z pytania 22).

3. Ciała działające na siebie siłą F(r)=C/r² poruszają się w jednej płaszczyźnie, a ich tory są krzywymi stożkowymi.

Pytanie 25.

Załóżmy, że na ciało o masie spoczynkowej m₀ i prędkości v=0 zaczyna działać stała siła
. Praca tej siły będzie równa Ek tego ciała. Elementarna praca wykonywana przez
przy przesunięciu ciała o
:
Szybkość wykonywania tej pracy wynosi:

Z II zasady dynamiki
stąd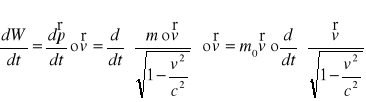
=>
=>
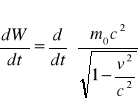
, stąd wynika równość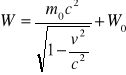

gdzie W₀ - jest stałą. Ponieważ W=Ek , Ek=0 dla v=0

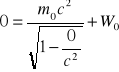
=> 0=m₀c²+W₀ => W₀ = - m₀c²

Zatem energia kinetyczna relatywistyczna wyraża się wzorem: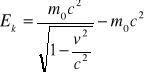

Więc: Ek=E-E₀ => E=Ek+E₀ gdzie E₀ = m₀c² jest energią spoczynkową.

Całkowita energia ciała:

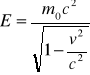
E=mc² ,gdzie m jest masą relatywistyczną

Pytanie 26.

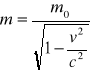
Gdy ciało znajduje się na poziomie odniesienia takim, że Ep=0, wówczas E=mc² . Związek ten wyraża zasadę równoważności masy i energii, według której każdej masie m przypisuje się energię mc² i każdej energii E przypisuje się pewną masę : m=E/c² . Zasada ta łączy zasadę zachowania energii i zasadę zachowania masy w jedną ogólną zasadę zachowania energii (lub ogólną zasadą zachowania masy).

Pytanie 27.

Bryła sztywna może wykonywać:

a) ruch postępowy - opisujemy go podobnie jak ruch punktu materialnego. W szczególności obowiązuje II zasada dynamiki

środek

masy

b) ruch obrotowy - zależy od rozkładu masy względem osi obrotu

Pytanie 28.

Moment bezwładności I bryły sztywnej:

Jednostka [kg*m²].

W układzie współrzędnych Δm_j posiada współrzędne (x_j ;y_j ;z_j). Wówczas I - jest tensorem 2-go stopnia, czyli jest opisany przez 9 współrzędnych:

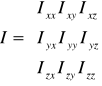
Jest to tensor symetryczny I_xy=I_yx, I_xz=I_zx, I_yz=I_zy

Do ciągłego rozkładu masy:
,gdzie r- odległość elementarnej masy od osi obrotu

a) moment bezwładności jednorodnego pręta:

b) moment bezwładności pełnego walca:

c) moment bezwładności kuli:

d) moment bezwładności obręczy:

ad8)M i M:

prędkość światła jest stała i nie zależna od ruchu układu odniesienia.począwszy od roku 1881M. i M. wykonali za pomocą

---