1

-Tw. Bettiego o wzajemności prac. Suma prac wirtualnych układów sił P­_i na odpowiadających na przemieszczeniach wywołanych przez układu sił P_j równa się sumie prac wirtualnych układu sił P_j na przemieszczeniach wywołanych układu sił P_i.

Tw. Maxwella o wzajemności przemieszczeń. Przemieszczenie pkt. Zaczepienia siły P_i wywołane przez siłę P_j i zrzutowane na kierunek działania siły P_i oraz przemieszczenie pk. zaczepienia siły P_i i zrzutowane na kierunek działania siły P_j są sobie równe, jeżeli P_i=P_j

2. Twierdzenie Castigliano i Menabrea - Castigliano

-Tw. Castigliano i jego zast. w obliczaniu przemieszczeń. Pochodna cząstkowa całkowitej energii sprężystej układu liniowo sprężystego względem siły ogólnejdziałającej w danym pkt. równe jest przemieszczeniu tego pkt. W kierunku działającej siły.

żnak + zwrot zgodny z kierunkiem działania siły, znak - niezgodny z kierunkiem działającej siły.

Tw. Menabrea - Castigliano.

W układzie liniowo sprężystym sztywnie podpartym pochodna cząstkowa energii sprężystej całego układu względem wielkości podporowej - hiper statycznej jest równa zero.

3. Metoda Maxwella-Mohra

Twierdzenie Maxwella-Mohra .

Uogólnieone przemieszczenie f_i wynosi
Fi - uogólniona siła Fi

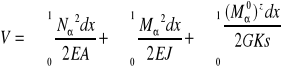
energia sprężysta

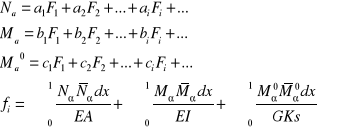
wzór Maxwela Mohra

_{siły wewnętrzne}

_{4 ????????????????????????????????????????}

_{5???????????????????????????}

_{629. Wytężenie materiału. Hipotezy wytężeniowe}

Pojęcie wytężenia materiału.

Ogół zmian w stanie fizycznym ciała prowadzący do powstania trwałych odkształceń i zniszczenia spójności określono jako wytężenie. Stawia się hipotezę, że można utworzyć funkcję W określającą wytężenie. Jej argumentem są składowe stanu ośrodka ciągłego w danym punkcie (z reguły składowe stanu naprężenia σ_X , ..., _XY , ...) i parametry charakteryzujące materiał (C₁,...)

W=F(σ_X , ..., _XY ,...,C₁ ,...)

Naprężenie redukowane.

Naprężenie zredukowane odpowiada danemu stanowi naprężenia i jest porównywalne z jednokierunkowym stanem naprężenia.

Wytężenie to zagadnienie odpowiedności trój- lub dwukierunkowego stanu naprężenia z jednokierunkowym stanem naprężenia.

Hipotezy wytężenia.

1)Hipoteza największego naprężenia normalnego (Galileusz i Leibnitz). O wytężeniu decyduje max. naprężenie normalne (rozciągające lub ściskające)

a) Przestrzenny stan naprężenia.

σ₁ <= σ_zr , σ₂ <= σ_zr , σ₃ <= σ_zr

σ_zc <= σ₁ <= σ_zr , σ_zc <= σ₂ <= σ_{zr ,}

σ_zc <= σ₃ <= σ_zr

b)Płaski stan naprężenia σ₃ = 0

σ_zc <= σ₁ <= σ_{zr ,}

σ_zc <= σ₂ <= σ_zr

c)Ścinanie

_max = σ

σ_zc <= _max <= σ_zr

2)Hipoteza najwiekszych odkształceń właściwych (de Saint-Vermont)

O wytężeniu decydują odkształcenia (wydłużenie właściwe)

₁ <= _zr , ₂ <= _zr , ₃ <= _zr , _zc <= ₁ <= _zr

3)Hipoteza największych naprężeń stycznych

O wytężeniu decyduje

max. naprężenie

styczne

_max = (σ_max - σ_min) /2

a)Rozciąganie osiowe - _max = σ_red /2

b)Ogólny stan naprężenia - σ_red = σ_max - σ_min

-σ_zr <= σ_max - σ_min <= σ_zr

-σ_zr <= σ₁ - σ₂ <= σ_zr

-σ_zr <= σ₂ - σ₃ <= σ_zr

c)Płaski stan naprężenia - σ₃ = 0

-σ_zr <= σ_max - σ_min <= σ_zr

- różne znaki σ_x , σ_y

σ_x σ_y <= _xy²

- te same znaki σ_x , σ_y

σ_x σ_y > _xy²

Szczególne przypadki:

I) σ_x = σ , σ_y = 0 , _xy =  →

II)Ścinanie

_xy =  , σ_x = 0 , σ_y = 0 →

4)Hipoteza energetyczna

a)Miara wytężenia - całkowita energia sprężysta (Huber,Beltrami)

b)Miara wytężenia - energia odkształcenia postaciowego (Huber,Ses)

Dla dowolnego stanu naprężenia spowodowanego rozciąganiem:

_f = (1+) /6E [(σ_x -σ_y)²+(σ_y -σ_z)²+(σ_z -σ_x)²+

+6(_xy² +_yz² +_zx²)]-energia odkszt.postac.

Dla płaskiego stanu naprężeń: σ_z = _yz = _zx = 0

Szczególne przypadki:

I) σ_x = σ , σ_y = 0 , _xy =  ,

2. _{Ścinanie: σx ,σy = 0 , xy =  ,}
   

_{7 ?}

_{8 ZDJECIE}

_{9 ZDJECIE}

_10ZDJECIE

_11?

_12?

_13?