STATYSTYKA - ZMIENNA LOSOWA
Charakterystyki funkcyjne i liczbowe zmiennej losowej typu skokowego:
Rozkład prawdopodobieństwa: P(X=xi)=pi ![]()
Dystrybuanta: F(X)=P(X<x)=![]()
Własności dystrybuanty: 1. F(-∞)=0
2. F(+∞)=1
3. 0≤F(X) ≤1 (musi być przynajmniej lewostronnie ciągła)
Wartość oczekiwana (nadzieja matematyczna): ![]()
Wariancja: ![]()
Teoretyczne rozkłady zmiennej losowej typu skokowego:
Rozkład zero-jedynkowy:
Rozkład dwumianowy (Bernoulli'ego):
Rozkład Poisson'a:
Charakterystyki funkcyjne i liczbowe zmiennej losowej typu ciągłego:
Teoretyczne rozkłady zmiennej losowej typu ciągłego:
Rozkład normalny LaPlace'a:
Rozkład normalny wystandaryzowany:
Rozkład Chi2:
Rozkład t-Studenta:
Szacowanie średniej populacji generalnej:
Twierdzenie 1:
Twierdzenie 2:
Twierdzenie 3 (tzw. Twierdzenie graniczne):
Twierdzenie 4:
Szacowanie odchylenia standardowego w zbiorowości generalnej:
P(X=1)=p P(X=0)=q
E(X)=p
D2(X)=pq
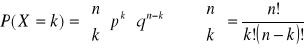
E(X)=np
D2(X)=npq
![]()
E(X)=λ
D2(X)=λ
Funkcja gęstości: 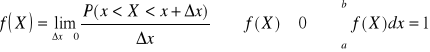
Dystrybuanta: F(X)=P(X<x) 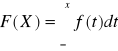
f(t) - funkcja gęstości
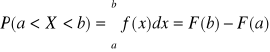
Wartość oczekiwana: 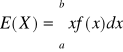
Wariancja: 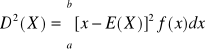
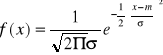
E(X)=m
D2(X)=σ2
D(X)= σ
X: N(m, σ)
![]()
![]()
U: N(0;1)
Ui: N(0;1)
![]()
E(χ2)=k
D2(χ2)=2k
![]()
E(t)=0
![]()
Przedział ufności: 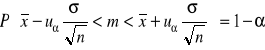
Błąd oszacowania: ![]()
Niezbędna liczebność próby: ![]()
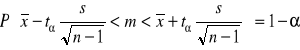
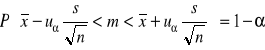
![]()
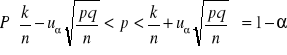
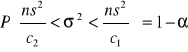
c1 odczytujemy dla ![]()
c2 odczytujemy dla ![]()
Wyszukiwarka
Podobne podstrony:
Kordecki W, Jasiulewicz H Rachunek prawdopodobieństwa i statystyka matematyczna Przykłady i zadania
RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA MATEMATYCZNA wprowadzenie
Rachunek prawdopodobieństwa, akademia ekonomiczna, semestr I, statystyka matematyczna
Kotłowska M Rachunek prawdopodobieństwa i statystyka matematyczna
Rachunek prawdopodobienstwa-1, Statystyka matematyczna
Wykład 3- Teoria prawdopodobieństwa i statystyki matematycznej, socjologia, statystyka
Rachunek prawdopodobieństwa i statystyka matematyczna, wykład 3
Podstawy statystyki - zadania, budownictwo pwr, Rachunek prawdopodobieństwa i statystyka matematyczn
Zadanie 3, Niezawodność konstr, niezawodność, Niezawodność konstrukcji, 1-Rachunek prawdopodobieństw
Rachunek prawdopodobieństwa i statystyka matematyczna, wykład 2
Zadanie 2 - arkusz, kbi, niezawodność, Niezawodność konstrukcji, 1-Rachunek prawdopodobieństwa i sta
Zadanie 1, Niezawodność konstr, niezawodność, Niezawodność konstrukcji, 1-Rachunek prawdopodobieństw
Krysicki Rachunek prawdopodobieĹ stwa i statystyka matematyczna cz 1
Stayst Stos 1, Rachunek Prawdopodobie?stwa i Statystyka Matematyczna
Zadanie 2, Niezawodność konstr, niezawodność, Niezawodność konstrukcji, 1-Rachunek prawdopodobieństw
Statyst Stos 2, Rachunek Prawdopodobie?stwa i Statystyka Matematyczna
Kordecki W, Jasiulewicz H Rachunek prawdopodobieństwa i statystyka matematyczna Przykłady i zadania
Probabilistyka Procesy stochastyczne Statystyka matematyczna Rachunek prawdopodobienstwa e 0c48
Krysicki i inni Rachunek prawdopodobienstwa i statystyka matematyczna w zadaniach cz I
więcej podobnych podstron