Zad.2. Wyznaczyć sumę 10 początkowych wyrazów ciągu arytmetycznego ![]()
mając dane ![]()
Ciągi liczbowe.
Zad.1. Obliczyć sumę wszystkich nieparzystych liczb naturalnych mniejszych
od 500.
Zad.2. Wyznaczyć sumę 10 początkowych wyrazów ciągu arytmetycznego ![]()
mając dane ![]()
Zad.3. Znaleźć ciąg arytmetyczny , w którym suma trzech początkowych wyrazów jest równa 27, natomiast suma kwadratów tych wyrazów jest równa 275.
Zad.4. Obliczyć sumę początkowych dwudziestu liczb naturalnych , które przy dzieleniu przez 7 dają resztę 3.
Zad.5. Znaleźć ciąg arytmetyczny , którego pierwszy wyraz jest równy 1,
a suma początkowych pięciu wyrazów jest cztery razy mniejsza od sumy następnych pięciu wyrazów.
Zad.6.Dany jest ciąg ![]()
. Wykazać , że jest on ciągiem arytmetycznym. Obliczyć sumę n początkowych wyrazów ciągu.
Zad.7. Logarytmy liczb ![]()
tworzą ciąg arytmetyczny. Obliczyć x.
Zad.8. Rozwiązać równanie :
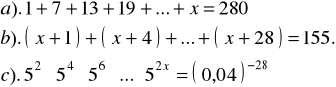
Zad.9. Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny
o .różnicy 2. Obliczyć pole koła wpisanego w ten trójkąt.
Zad.10. Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny.
Obliczyć długości przyprostokątnych , jeżeli wiadomo , że długość przeciwprostokątnej wynosi 30 cm.
Zad.11. Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny.
Wykazać, że różnica tego ciągu jest równa długości promienia okręgu wpisanego w ten trójkąt.
Zad.12. Między liczby 32 i 500 wstawić liczby x i y tak dobrane, aby ciąg
( 32, x, y, 500) był ciągiem geometrycznym.
Zad.13. Trzy liczby, których suma jest równa 93 tworzą ciąg geometryczny.
Te same liczby możemy uważać za pierwszy, drugi i siódmy wyraz ciągu arytmetycznego. Znaleźć te trzy liczby.
Zad.14. Udowodnić, że jeżeli liczby dodatnie a, b i c tworzą ciąg geometryczny, to ich logarytmy tworzą ciąg arytmetyczny.
Zad.15. Liczby a i b są pierwiastkami równania x2-3x+A=0 , a liczby c i d są pierwiastkami równania x2-12x+B=0.. Ciąg ( a , b , c , d ) jest rosnącym ciągiem geometrycznym . Obliczyć A i B .
Zad.16. Z czterech liczb trzy pierwsze tworzą ciąg geometryczny, a trzy ostatnie ciąg arytmetyczny. Znaleźć te liczby , jeżeli wiadomo , że suma pierwszej i ostatniej liczby jest równa 14, a suma liczb środkowych jest równa 12.
Zad.17. Dla jakich wartości parametru m. liczby x , y , z będące rozwiązaniem układu równań
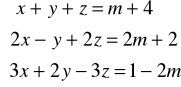
są trzema kolejnymi wyrazami ciągu geometrycznego ?
Zad.18. Rozwiązać równanie :
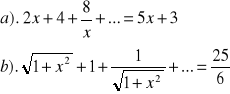
Zad.19 Wyznacz wszystkie wartości ![]()
, dla których pierwiastki wielomianu ![]()
są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.
Zad.20 Dany jest ciąg geometryczny ![]()
, w którym ![]()
wyznacz wzór na n-ty wyraz ciągu ![]()
,
Oblicz x, jeśli wiadomo, że liczby ![]()
, 3x + 2 tworzą ciąg arytmetyczny.
Zad.21. Znaleźć szereg geometryczny o sumie ![]()
mający tę własność , że szereg utworzony z kwadratów jego wyrazów ma sumę ![]()
.
Zad.22. W nieskończonym ciągu geometrycznym, którego suma jest równa ![]()
, pierwszy wyraz ![]()
,a trzeci jest odwrotnością pierwszego. Obliczyć x
Zad.24. Rozwiązać nierówność :
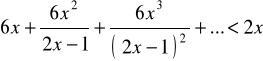
, której lewa strona jest sumą nieskończonego ciągu geometrycznego.
Zad.25. W kwadracie o boku a połączono odcinkami środki sąsiednich boków. W powstałym w ten sposób kwadracie połączono znów środki sąsiednich boków itd. Obliczyć sumę obwodów utworzonego w ten sposób nieskończonego ciągu kwadratów.
Zad.26. Sinusy katów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ciąg geometryczny. Oblicz sinus najmniejszego kąta ostrego.
Zad.27
Wyznacz x, tak aby liczby ![]()
były w podanej kolejności wyrazami rosnącego ciągu geometrycznego o wyrazach całkowitych.
Zad.28
Ciąg ![]()
jest arytmetyczny. Wiedząc, że ![]()
wyznacz różnicę tego ciągu.
Zad.29
Wykaż, że jeżeli liczby ![]()
są kolejnymi wyrazami ciągu geometrycznego, to liczby ![]()
są kolejnymi wyrazami ciągu arytmetycznego.
Zad.30
Dany jest ciąg ![]()
. Ciąg ![]()
ma tę własność, że dla każdego ![]()
punkty o współrzędnych ![]()
leżą na jednej prostej. Wyznacz wzór ogólny ciągu ![]()
Zad.31
Długości boków trójkąta prostokątnego są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego. Oblicz iloraz tego ciągu.