Jelenia Góra, 27.03.2000r.
Teoria obwodów 2
-laboratorium
Temat ćwiczenia:
STANY NIEUSTALONE
data wykonania ćwiczenia: 20.03.2000r.
grupa laboratoryjna: PONIEDZIAŁEK GODZ. 12.00
wykonali: Anna Miedzianowska
Sławomir Kukiełka
CZĘŚĆ TEORETYCZNA
Stanem ustalonym nazywa się stan równowagi układu, w którym parametry charakteryzujące reakcję np. wartość maksymalna, częstotliwość, faza początkowa nie zmieniają się w czasie .
Komutacja jest to zaburzenie istniejącego stanu ustalonego wywołane np. włączeniem lub wyłączeniem źródła, zmianą połączeń lub wartości elementów. Każda komutacja powoduje zaburzenie istniejącego stanu ustalonego. Nowy stan ustalony nie może wystąpić natychmiastowo, lecz jest poprzedzony występowaniem pewnego stanu przejściowego.
Stan przejściowy w istniejący w układzie podczas przejścia z jednego stanu ustalonego w drugi nazywamy stanem nieustalonym.
Występowanie stanu nieustalonego jest spowodowane istnieniem energii zmagazynowanej w cewkach i kondensatorach. Energia ta podczas przejścia z jednego stanu ustalonego w drugi może zmieniać się tylko w sposób ciągły, gdyż zmiany skokowe powodowałyby występowanie w układzie nieskończenie wielkich prądów lub napięć.
Z zasady ciągłości zmian prądów w cewkach i napięć na kondensatorach wynika, że wartości tych wielkości tuż po komutacji pozostają takie same jak przed komutacją, a następnie zmieniają się płynnie .
Teoretycznie układ osiąga stan ustalony po upływie czasu nieskończenie długiego. W praktyce wyznacza się tzw. czas ustalania się (tu), po upływie którego przyjmuje się, że układ jest w stanie ustalonym. Wyznacza się także tzw. stałą czasową, która charakteryzuje szybkość zanikania przebiegu przejściowego.
Celem ćwiczenia jest:
obserwacja stanów nieustalonych w obwodach pierwszego i drugiego rzędu przy pobudzeniu jednostkowym,
pomiar wielkości charakteryzujących reakcje układów w stanach nieustalonych,
porównanie wyników pomiarów i obserwacji z wynikami uzyskanymi z analizy teoretycznej.
W ćwiczeniu zbadaliśmy:
układ pierwszego rzędu RC,
układ pierwszego rzędu RL,
układ drugiego rzędu RLC,
1. UKŁAD PIERWSZEGO RZĘDU RC
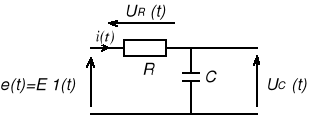
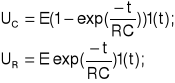
1.1. Przy wybranej pojemności (C3) przerysowaliśmy oscylogramy napięcia Uc dla trzech różnych wartości rezystancji R (R1, R1 || R2 oraz R2 || R3). Z nich odczytaliśmy stałą czasową oraz czas ustalania się (→wykresy 1.1.A÷C).
R |
C |
τ[ms] |
tu[ms] |
R1 |
C3 |
0,66 |
1,25 |
R1||R2 |
C3 |
0,23 |
0,5 |
R2||R3 |
C3 |
0,1 |
0,38 |
Dla ostatniego przypadku --> [Author:AM] przerysowaliśmy oscylogram napięcia Ur. Z niego również odczytaliśmy stałą czasową i czas ustalania się (→wykres 1.1.D).
R |
C |
τ[ms] |
tu[ms] |
R2||R3 |
C3 |
0,1 |
0,34 |
1.2. Przy wybranej rezystancji R1 przerysowaliśmy oscylogramy napięcia Uc dla trzech różnych wartości pojemności C: C1, C2 oraz C3. Z nich odczytaliśmy stałą czasową oraz czas ustalania się (→wykresy 1.2.A÷C).
R |
C |
τ[ms] |
tu[ms] |
R1 |
C1 |
0,04 |
0,25 |
R1 |
C2 |
0,2 |
0,75 |
R1 |
C3 |
0,66 |
1,4 |
Dla pierwszego przypadku --> [Author:AM] przerysowaliśmy oscylogram napięcia Ur. Z niego również odczytaliśmy stałą czasową i czas ustalania się (→wykres 1.2.D).
R |
C |
τ[ms] |
tu[ms] |
R1 |
C1 |
0,04 |
0,09 |
1.3. Ponieważ dla rozważanego układu τ=RC, na podstawie pomiarów 1.1 obliczyliśmy wielkość C3:
R |
τ[ms] |
C3 [μF]=τ/R |
3900 |
0,66 |
C3=3900/0,66=0,169 |
1322,034 |
0,23 |
C3=1322,034/0,23=0,174 |
581,560 |
0,1 |
C3=581,56/0,1=0,172 |
Na podstawie pomiarów 1.2 obliczyliśmy wielkości C1, C2, C3:
R1 |
τ[ms] |
C [μF] =τ/R1 |
3900 |
0,04 |
C1=3900/0,04=0,010 |
3900 |
0,2 |
C2=3900/0,2=0,051 |
3900 |
0,66 |
C3=3900/0,66=0,169 |
Przyjmujemy dalej, że:
C1=10 nF,
C2=51 μF,
C3=0,17 μF.
1.4. Ponieważ oscylogramy, które przerysowaliśmy z oscyloskopu nie są zbyt dokładne, na wykresach 1.4A÷C przedstawiliśmy analizę teoretyczną badanego układu.
Na wykresie A przedstawiliśmy wpływ C na przebieg Uc, czyli przy ustalonym R zmienialiśmy C.
Na wykresie B badaliśmy wpływ R, czyli przy ustalonej wartości C zmienialiśmy R.
Na wykresie C przedstawiliśmy połączenie wartości ekstremalnych.
2. UKŁAD PIERWSZEGO RZĘDU RL
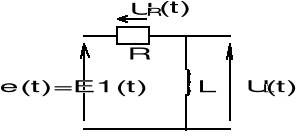
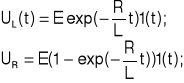
2.1. Przy wybranej indukcyjności(L1) przerysowaliśmy oscylogramy napięcia UL dla trzech różnych wartości rezystancji R (R1, R2, R3). Z nich odczytaliśmy stałą czasową oraz czas ustalania się (→wykresy 2.1A÷C)
R |
L |
τ[ms] |
tu[ms] |
R3 |
L1 |
0,12 |
0,14 |
R2 |
L1 |
0,05 |
0,09 |
R1 |
L1 |
0,03 |
0,08 |
Dla przypadku --> [Author:AM] R3+L1 przerysowaliśmy oscylogram napięcia Ur. Z niego również odczytaliśmy stałą czasową i czas ustalania się.
R |
L |
τ[ms] |
tu[ms] |
R3 |
L1 |
0,12 |
0,19 |
2.2. Przy wybranej rezystancji R1 przerysowaliśmy oscylogramy napięcia UL dla trzech różnych wartości indukcyjności L: (L1, L2, L3). Z nich odczytaliśmy stałą czasową oraz czas ustalania się (→wykresy 2.2A÷C).
R |
L |
τ[ms] |
tu[ms] |
R1 |
L1 |
0,03 |
0,1 |
R1 |
L2 |
0,01 |
0,03 |
R1 |
L3 |
0,002 |
0,01 |
Dla pierwszego przypadku --> [Author:AM] przerysowaliśmy oscylogram napięcia Ur. Z niego również odczytaliśmy stałą czasową i czas ustalania się (→wykres 2.2D).
R |
L |
τ[ms] |
tu[ms] |
R1 |
L1 |
0,08 |
0,19 |
2.3. Ponieważ dla rozważanego układu τ=L/R, na podstawie pomiarów 2.1 obliczyliśmy wielkość L1:
R |
τ[ms] |
L1[mH]=τ⋅R |
820 |
0,12 |
L1=820⋅0,12=98,4 |
2000 |
0,05 |
L1=2000⋅0,05=100 |
3900 |
0,025 |
L1=3900⋅0,025=97,5 |
Na podstawie pomiarów 2.2 obliczyliśmy wielkości L1, L2, L3:
R1 |
τ[ms] |
L[mH] =τ⋅R1 |
3900 |
0,025 |
L1=3900⋅0,025=97,5 |
3900 |
0,01 |
L2=3900⋅0,01=39 |
3900 |
0,003 |
L3=3900⋅0,003=11,7 |
Przyjmujemy dalej, że:
L1=98 mH,
L2=39 mH,
L3=12 mH.
2.4. Ponieważ oscylogramy, które przerysowaliśmy z oscyloskopu są niedokładne, na wykresach 2.4A÷C przedstawiliśmy analizę teoretyczną dla badanego układu.
Na wykresie A przedstawiliśmy wpływ L na przebieg UL, czyli przy ustalonym R zmienialiśmy L.
Na wykresie B badaliśmy wpływ R, czyli przy ustalonej wartości L zmienialiśmy R.
Na wykresie C przedstawiliśmy połączenie wartości ekstremalnych.
3. UKŁAD DRUGIEGO RZĘDU RLC
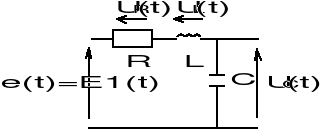
3.1. Przy zmianie rezystancji układu dla pojemności C2 i indukcyjności L2 otrzymywaliśmy 3 różne odpowiedzi układu na pobudzenie jednostkowe: aperiodyczną dla R1, aperiodyczną krytyczną dla R2 i oscylacyjną dla R1||R2||R3.
L |
C |
R |
2√L/√C |
przypadek |
L2 |
C2 |
R1=3900> |
1748,95 |
aperiodyczny |
L2 |
C2 |
R2=2000≈ |
1748,95 |
aperiodyczny- krytyczny |
L2 |
C2 |
R1||R2||R3=506,09< |
1748,95 |
oscylacyjny |
Dla wszystkich przypadków przerysowaliśmy oscylogramy napięcia Uc (→wykresy 3.1A÷C) i UL (→wykresy 3.1D÷F). Z nich odczytaliśmy czas ustalania się.
L |
C |
R |
tu(Uc) |
tu(UL) |
L2 |
C2 |
R1=3900 |
0,7 |
0,36 |
L2 |
C2 |
R2=2000 |
0,6 |
0,29 |
L2 |
C2 |
R1||R2||R3=506,09 |
0,8 |
0,4 |
3.2. Dla indukcyjności L2 i każdej pojemności C dobraliśmy R tak, aby zawsze otrzymać przypadek oscylacyjny.
L |
C |
2√L/√C |
R1||R2||R3 |
przypadek |
L2 |
C1 |
3938,3> |
506,093 |
oscylacyjny |
L2 |
C2 |
1726,38> |
506,093 |
oscylacyjny |
L2 |
C3 |
945,58> |
506,093 |
oscylacyjny |
Dla wszystkich wartości C przerysowaliśmy oscylogramy napięcia Uc (→wykresy 3.2A÷C). Z nich odczytaliśmy czas ustalania się.
L |
C |
R1||R2||R3 |
tu |
L2 |
C1 |
506,093 |
0,5 |
L2 |
C2 |
506,093 |
0,5 |
L2 |
C3 |
506,093 |
0,5 |
3.3. Na wykresach 3.3A÷C przedstawiliśmy trzy przypadki odpowiedzi układu RLC dla danych teoretycznych.
WNIOSKI
W ćwiczeniu zajęliśmy się badaniem stanów nieustalonych w układach RC, RL i RLC przy pobudzeniu sygnałem prostokątnym.
Badając układ pierwszego rzędu RC doszliśmy do następujących wniosków:
im większa pojemność, tym dłuższy czas ustalania się (i większa stała czasowa)
im większa rezystancja, tym dłuższy czas ustalania się (i większa stała czasowa)
Dla wszystkich oscylogramów wyznaczyliśmy stałą czasową i czas ustalania się. Dla największej rezystancji (3900Ω) czas ustalania się wynosił 0,66ms, a dla najmniejszej badanej rezystancji (581Ω) jedynie 0,1. Przy zmianie pojemności, dla maksymalnej czas ustalania wynosił 1,4ms, a dla minimalnej 0,25ms. Widać stąd, że w badanym układzie zmiana pojemności ma większy wpływ na ustalanie się niż zmiana rezystancji.
Wnioski te poparliśmy analizą teoretyczną. Do jej wykonania obliczyliśmy wartości wszystkich elementów C (przyjęliśmy je z pewnym przybliżeniem).
Badając układ pierwszego rzędu RL doszliśmy do następujących wniosków:
im większa indukcyjność, tym dłuższy czas ustalania się i większa stała czasowa
im większa rezystancja, tym krótszy czas ustalania się i większa stała czasowa
zmiana indukcyjności ma większy wpływ na ustalanie się niż zmiana rezystancji.
Dla wszystkich oscylogramów wyznaczyliśmy stałą czasową i czas ustalania się. Dla największej rezystancji (3900Ω) stała czasowa wynosiła jedynie 0,03 ms, podczas gdy dla najmniejszej rezystancji (581Ω) aż 0,1. Przy zmianie indukcyjności największa stała czasowa wyniosła 0,1 (dla największej indukcyjności), a najmniejsza 0,01(dla najmniejszej indukcyjności).
Wnioski te poparliśmy analizą teoretyczną, obliczając w sposób analogiczny do poprzedniego przypadku wartości elementów L (również w przybliżeniu).
Przy porównaniu układów pierwszego rzędu RC i RL należy zauważyć, że rola rezystancji jest różna w obu przypadkach. Dla układu RC zwiększenie rezystancji powoduje zwiększenie stałej czasowej (a tym samym czasu ustalania się), a w układzie RL jest dokładnie odwrotnie.
Odpowiedź układu drugiego rzędu RLC na pobudzenie jednostkowe nie była jednakowa dla dowolnych wartości elementów układu. Jeżeli spełniony był warunek 2√L/√C<R to mieliśmy do czynienia z odpowiedzią aperiodyczną, jeżeli 2√L/√C=R z odpowiedzią aperiodyczną krytyczną, a w przeciwnym wypadku z odpowiedzią oscylacyjną.
Przypadek krytyczny jest przypadkiem, w którym aperiodyczne przebiegi prądu i napięć osiągają wartości ustalone w najkrótszym czasie, ale kształt przebiegu Uc i UL w zasadzie nie różni się od odpowiedzi aperiodycznej. W naszym ćwiczeniu zbadaliśmy przypadek krytyczny jedynie w przybliżeniu, gdyż nie mogliśmy dobrać elementów układu tak, aby idealnie zachodziła równość R=2√L/√C. Niemniej jednak czas ustalania się był dla tego przypadku najkrótszy. Najdłuższy czas zanotowaliśmy dla przypadku oscylacyjnego.
Następnie zbadaliśmy wpływ rezystancji na odpowiedzi układu. Dobraliśmy takie wartości L i C, że przy zmianie R otrzymywaliśmy trzy różne odpowiedzi układu- aperiodyczną, aperiodyczną-krytyczną i oscylacyjną.
W następnej kolejności zbadaliśmy wpływ pojemności na oscylacje układu, czyli dla dobranych L i R zmienialiśmy pojemność. Po zbadaniu odpowiedzi, nasuwają się następujące wnioski:
-im większa pojemność tym więcej oscylacji
-im większa pojemność tym większe są amplitudy oscylacji
Stwierdziliśmy także, że zmiana pojemności nie wpłynęła znacząco na czas ustalania.
Wyniki naszych pomiarów porównaliśmy z teoretycznymi przebiegami. Z analizy teoretycznej wynika, że czasy ustalania się napięć powinny być nieco inne niż te, które odczytaliśmy z oscylogramów. Jest to najprawdopodobniej spowodowane tym, że w układzie wpływ na odpowiedź ma również rezystancja wewnętrzna generatora, której nie uwzględniliśmy w obliczeniach teoretycznych, a powoduje ona zwiększenie stałej czasowej w przypadku układu RC, a zmniejszenie w RC.
W każdym przypadku przebiegi te różniły się od siebie w mniejszym lub większym stopniu. Różnice te nie byłyby tak znaczne, gdybyśmy mieli do dyspozycji oscyloskop cyfrowy z pamięcią podłączony do komputera z drukarką. Nie musielibyśmy przerysowywać oscylogramów co wprowadza dość duży błąd, (niezauważalny na pierwszy rzut oka), ale w konsekwencji wpłynęło negatywnie na jakość obliczeń. Ćwiczenie przebiegałoby sprawniej a pomiary byłyby dokładniejsze, a zatem bardziej przydatne.
- 9
Stany nieustalone
nie wiem jaka to wartość
nie wiem jaka to wartość
nie wiem jaka to wartość
nie wiem jaka to wartość
Chyba UL
tego chyba nie
tego chyba nie
Wyszukiwarka
Podobne podstrony:
8) Szeregi Fouriera, sPRAWOZDANIE8, Jelenia Góra, 22
4) Obwody rezonansowe, Sprawozdanie4, Jelenia Góra, 10
Plakat JELENIA GORA Przyjazdy wazny od 2014 04 27 do 2014 06 14
wzor oferty tablice, Przegrane 2012, Rok 2012, mail 27.06 Jelenia Góra tablice
8) Szeregi Fouriera, sPRAWOZDANIE8-kopia, Jelenia Góra, 22
Plakat JELENIA GORA Przyjazdy wazny od 2014 04 27 do 2014 06 14
Plakat JELENIA GORA Odjazdy wazny od 2014 04 27 do 2014 06 14
08 Stany nieustalone w obwodach RLCid 7512 ppt
SPRAWKO STANY NIEUSTALONE, Elektrotechnika, Elektrotechnika
stany nieustalone w RC, Elektrotechnika-materiały do szkoły, Elektrotechnika
Ceny biletów kolejowych dla studentów na trasie Jelenia Góra Wrocław Główny
Ceny biletów kolejowych dla uczniów na trasie Jelenia Góra Poznań Główny
03 stany nieustalone
C7a Stany nieust RLC 2012
instrukcja - stany nieustalone, Elektrotechnika AGH, Semestr III zimowy 2013-2014, semestr III, seme
więcej podobnych podstron