Zadania: Dynamika ruchu obrotowego, warunki równowagi

1. Oblicz moment bezwładności molekuły CO₂ względem osi przechodzącej przez środek masy i prostopadłej do osi molekuły. Molekuła jest liniowa z atomem C znajdującym się w jej środku. Długość wiązania C—O wynosi, 1,13*10^-10m. Liczba Avogadra N_A = 6,02*10²³ 1/mol. (I = 6,8 * 10^-46 kgm²)

2. Wykaż, że moment bezwładności układu składającego się z dwóch mas m₁ i m₂ odległych o r od siebie względem osi prostopadłej do odcinka łączącego m₁ i m₂ i przechodzącej przez środek masy układu wynosi
   . Gdzie
   jest masą zredukowaną układu i wynosi:
   .

3. Wyznacz moment bezwładności drobiny CO względem osi przechodzącej przez środek masy i prostopadłej do osi molekuły. Długość wiązania C—O wynosi, 1,13*10^-10m. Obliczenia wykonaj dwoma sposobami; korzystając z definicji momentu bezwładności oraz stosując wzór z zadania 2. (I = 1,46 * 10^-46 kgm²)

4. Po torze w kształcie pętli o promieniu 50 cm ześlizguje się bez tarcia ciało o małych rozmiarach. Od jakiej najmniejszej wysokości mogło ono rozpocząć ruch, jeżeli nie odpada ono od toru w najwyższym jego punkcie? (2,5R)

5. Do pionowo zorientowanej osi przywiązany jest sznur o długości 1,5 m, na którego końcu przywiązane jest ciało o masie m = 200g. Układ ten wiruje z prędkością kątową 3,14 1/s.

1. Jaki kąt tworzy sznur z kierunkiem pionowym w czasie wirowania układu ? (48⁰)

2. Jakie jest naprężenie sznura ? (3 N)

6. Dane są dwie pełne kule A i B wykonane z tego samego materiału. Masa kuli A jest 8 razy większa od masy kuli B. Ile razy moment bezwładności kuli A jest większy od momentu bezwładności kuli B ? (32)

7. Na walcu o promieniu 5 cm i masie m_w = 1 kg: osadzonym na poziomej osi nawinięta jest nić. Na zwisającym końcu nici zawieszone jest ciało o masie m_c=200g.

1. Z jakim przyspieszeniem obniżać się będzie ciało po oswobodzeniu układu ? (2,8 m/s²)

2. Jakie jest naprężenie nici w czasie ruchu układu ? (1,4 N)

8. Na walcu o masie m = 200 g, przy jego końcach, w jednakowy sposób nawinięte są dwie nici, na których walec jest zawieszony w ten sposób, że jego oś jest zorientowana poziomo.

1. Z jakim przyspieszeniem obniżać się będzie oś walca po oswobodzeniu ? (6,5 m/s²)

2. Jak duże jest łączne naprężenie obydwu nici w czasie ruchu walca ? (0,65 N)

9. Okrągła platforma o masie 200 kg i promieniu 1,5 m wiruje wokół pionowej osi z częstotliwością 12 obr/min. Na brzegu platformy stoi człowiek o masie 60 kg. Jaka będzie częstotliwość wirowania jeżeli człowiek przejdzie do środka platformy ? (0,32 Hz)

10. Z równi pochyłej nachylonej do poziomu pod kątem 30° stacza się bez poślizgu jednorodny walec.

1. Jakie jest przyspieszenie ruchu postępowego jego osi ? (3,3 m/s²)

11. Po równi pochyłej, z wysokości h = 40 cm staczają się bez poślizgu walec i cienkościenny cylinder. Jaki jest stosunek ich czasów staczania się ? (0,85)

12. Na wspólnej osi, zorientowanej pionowo, osadzone są dwa jednakowe koła o masach 10 kg i średnicach 40 cm. Koło znajdujące się niżej połączone jest z osią i obraca się z prędkością kątową 25,12 1/s. Drugie koło początkowo nieruchome, zostaje nałożone na koło pierwsze. Współczynnik tarcia między powierzchniami kół równy jest f = 0,2.

1. Jaka będzie końcowa prędkość kątowa ich ruchu obrotowego ? (12,56 1/s)

2. * Po jak długim czasie od chwili skontaktowania kół ich prędkości kątowe ruchu obrotowego wyrównają się ?

13. * Środek masy kuli bilardowej posiada początkową prędkość V₀. Promień kuli wynosi R, jej masa M, a współczynnik tarcia pomiędzy kulą i stołem jest równy f. Jak daleko przesunie się kula po stole, zanim przestanie się ślizgać ?

14. Wyznacz wypadkową sił działających na punkt O, znając ich wartości oraz kąty, jakie tworzą z dodatnim kierunkiem osi x:

a) F1= 60 N, α1 = 60°; F2= 100 N, α2 = 30°; F3= 20 N, α3 = 135°; F4= 40 N, α4 = 0°;

b) F1= 50 N, α1 = 90°; F2= 110 N, α2 = 270°; F3= 60 N, α3 = 180°; F4= 84.85 N, α4 = 45°;

15. 
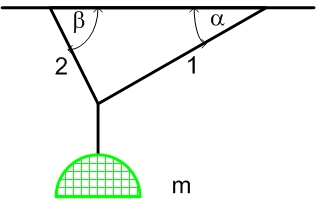
    Lampę o masie m=2 kg zawieszono na dwóch drutach tworzących z poziomem kąty α=30° i β=45°. Wyznacz siły naprężające druty.

16. Jednorodna kula o ciężarze W i promieniu R wisi na sznurku zaczepionym na gładkiej ścianie, w odległości L ponad środkiem kuli. Oblicz siłę naciągu sznurka i siłę wywieraną na kulę przez ścianę.

17. Drabina o długości L=20 m i masie m=30 kg opiera się o idealnie gładką ścianę. Środek ciężkości drabiny znajduje się w połowie jej wysokości. Współczynnik tarcia drabiny o podłogę 0,4. Znajdź graniczne położenie równowagi.

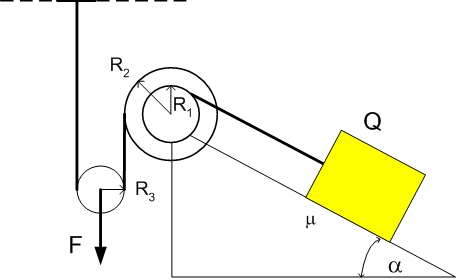
18. Skrzynię o ciężarze Q trzeba wciągnąć po pochylni na pewną wysokość. Zastosowano wciągarkę zbudowaną z układu lekkich krążków, jak pokazano na rysunku. Promienie krążków są znane, a skrzynia ma środek ciężkości w połowie wysokości. Jaką minimalną siłę F należy przyłożyć, jeżeli współczynnik tarcia skrzyni o pochylnię wynosi f ?

19. Dwoje ludzi niesie rurę o ciężarze 800 N i długości 5 m. Jeden z nich trzyma rurę w odległości 1 m od jej końca a drugi za przeciwległy koniec. Wyznacz obciążenie przypadające na każdego człowieka.

---