Politechnika Lubelska w Lublinie	Laboratorium Teorii Sterowania
Skład grupy:		Semestr	Grupa	Rok akad.
Temat ćwiczenia: Identyfikacja obiektów sterowania metodą charakterystyk czasowych.			Data wyk.	Ocena

1. Cel ćwiczenia.

Celem ćwiczenia jest zaobserwowanie i narysowanie odpowiedzi skokowej poszczególnych obiektów przy odpowiednim wyskalowaniu oscyloskopu oraz wstępnym określeniu parametrów wymuszenia.

2. Układ o transmitancji G1(s) na wymuszenie skoku jednostkowego.

Wykres odpowiedzi znajduje się na papierze milimetrowym.

Na podstawie odpowiedzi skokowej możemy stwierdzić, że układ pierwszy ma charakter członu różniczkującego o następującej transmitancji i stałej czasowej:

G(s) = k / (1 + sT)

T=1ms

k=1.3

3. Układ o transmitancji G2(s) na wymuszenie skoku jednostkowego.

Wykres odpowiedzi znajduje się na papierze milimetrowym.

Odpowiedź członu na skok jednostkowy wskazuje, że jest to obiekt oscylacyjny II rzędu.

G ( s ) = k / [ s²T² + 2ξTs + 1]

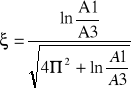
A1 = 2V A3 = 0,2·2V = 0,4V

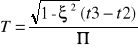
t3 = 2,3ms t2 = 1,5 ms

G ( s ) = k / [ s²T² + 2ξTs + 1],
, T = 0,76, k = 4

4. Układ o transmitancji G3(s) na wymuszenie skoku jednostkowego.

Wykres odpowiedzi znajduje się na papierze milimetrowym.

Na podstawie odpowiedzi obiektu na wymuszenie w postaci skoku jednostkowego stwierdzamy, że ma on postać układu inercyjnego pierwszego rzędu.

G ( s ) = k / [1 + sT ]

T = 2 ms

k = 1,25

5. Układ o transmitancji G3(s) na wymuszenie skoku jednostkowego.

Wykres odpowiedzi znajduje się na papierze milimetrowym.

Na podstawie odpowiedzi obiektu na wymuszenie w postaci skoku jednostkowego stwierdzamy, że ma on postać układu inercyjnego pierwszego rzędu.

G ( s ) = k / [1 + sT ]

T = 2 ms

k = 1,25

6. Wnioski

W ćwiczeniu tym dokonaliśmy identyfikacji obiektów sterowania metodą charakterystyk czasowych. Rozpoznanie układu umożliwiło opisanie go odpowiednim równaniem transmitancji operatorowej. Wyliczenie stałych k, współczynnika tłumienia ξ dla członu oscylacyjnego II rzędu może wiązać się z pewnymi błędami np. podczas rysowania stycznych do wykresu funkcji. Człon o transmitancji G1(s) to człon różniczkujący, człon o transmitancji G2(s) to człon oscylacyjny II rzędu, a ostatnia dwa czyli człon G3(s) i człon G4(s) to człony inercyjne pierwszego rzędu.

Obiekt	Identyfikacja
G1(s)	Człon różniczkujący
G2(s)	Człon oscylacyjny II rzędu
G3(s)	Człon inercyjny pierwszego rzędu
G4(s)	Człon inercyjny pierwszego rzędu

---