Kinematyka i Dynamika

Bogdan Wilczyński

Koszalin, 1994

Pojęcia podstawowe

Dynamika - badanie związków między ruchem ciał a siłami na to ciało działającymi.

Kinematyka - badanie ruchu ciał bez uwzględnienia przyczyn wywołujących ruch.

Ruch - zmiana połoźenia ciała względem innego ciała, zwanego ciałem odniesienia. Ciało odniesienia może być ruchome, lub nieruchome. Z ciałem odniesienia związany jest układ odniesienia (układ współrzędnych).

Ruch odbywa się w czasie i przestrzeni. Są to pojęcia pierwotne, których się nie definiuje.

Przestrzeń - przestrzeń trójwymiarowa, w szczególnym przypadku przestrzeń dwu- lub jednowymiarowa.

Czas - zbiór chwil, tak jak prosta składa się z punktów. Czas nie zależy od układu odniesienia, oraz jest nieograniczony, tzn. "płynie" od przeszłości do przyszłości.

Przedział czasu - gęsty i ciągły zbiór chwil zawarty między dwiema chwilami.

t = t2 - t1

t0 - chwila początkowa, zwykle t0 = 0.

Tor - linia jaką zakreśla w przestrzeni poruszający się punkt.

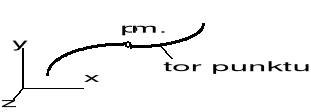
Rys.

Modele ciał materialnych

P-kt materialny Układ p-któw materialnych Ciało sztywne

Rys.

Kinematyka punktu materialnego (p.m.)

Sposoby opisu ruchu p.m.

Położenie punktu materialnego w przestrzeni Euklidesa (E3 ) opisujemy za pomocą:

1) współrzędnych naturalnych

2) współrzędnych kartezjańskich (prostokątnych)

3) promienia-wektora

4) współrzędnych biegunowych

5) innych współrzędnych, np. walcowych.

1) Opis ruchu w układzie naturalnym

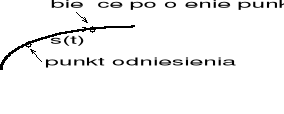
Rys.

2) Opis ruchu w układzie kartezjańskim jedno- dwu- lub trójwymiarowym

Ruch prostoliniowy. Do opisu położenia p.m. wystarczy układ jednowymiarowy Ox.

Ruch krzywoliniowy. Do opisu wystarczy układ dwuwymiarowy, jeśli ruch odbywa się w jednej płaszczyżnie, lub trójwymiarowy. Położenie punktu M na torze określają dwie (w przestrzeni trzy) współrzędne x i y zależne od czasu:

x = x(t) y = y(t)

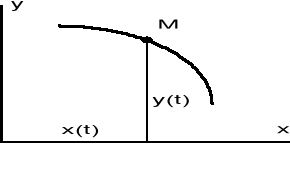
3) Opis ruchu za pomocą wektora-promienia r

Dany jest tor punktu M. Położenie tego punktu na torze, w dowolnej chwili t możemy opisać za pomocą wektora r wychodzącego z dowolnie obranego punktu (punkt, ciało odniesienia) O. Przy ruchu p-ktu M wektor r (wektor-promień) zmienia swój moduł i kierunek. Zmiana wektora r jest więc funkcją czasu t.

r = r(t)

tor punktu M (hodograf wektora r)

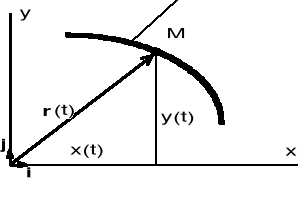
Z rys. mamy, że

r = r(t) = x i + y j, gdzie i, j - wersory.

Wyznaczanie prędkości i przyspieszeń

1) Gdy ruch jest opisany za pomocą wektora-promienia

Niech poruszający się punkt M znajduje się w chwili t w położeniu określonym wektorem r1, a w chwili t+t w położeniu M określonym wektorem r2 = r + r.

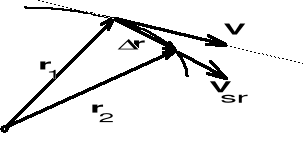
W czasie t wektor-promień r doznał przyrostu o wielkość r = r2 - r1. Stosunek przyrostu r do przyrostu t określamy jako prędkość średnią punktu

r/t = vśr

Wektor prędkości średniej jest skierowany wzdłuż wektora r. Przechodząc do granicy otrzymujemy wektor prędkości chwilowej v.

Def. Prędkość punktu jest wektorem określonym przez pierwszą pochodną wektora-promienia względem czasu, skierowanym wzdłuż stycznej do toru (hodografu wektora r).

Załóżmy, że w chwili t1 punkt znajduje się w położeniu M i ma prędkość v1, w chwili t2 w położeniu M i ma prędkość v2 , i.t.d.

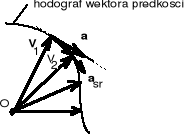
Obieramy dowolny biegun O i przenosimy doń równolegle wszystkie wektory prędkości. W czasie t nastąpił przyrost wektora prędkości o wielkość v. Stosunek przyrostu wektora prędkości v do przyrostu czasu t nazywamy przyspieszeniem średnim punktu:

v/t = aśr

Przechodząc do granicy otrzymujemy:

Ostatecznie:

a = v = r.

Uwaga! - pierwsza pochodna względem czasu, - druga pochodna względem czasu.

Przyspieszeniem nazywamy wektor dany przez pierwsza pochodną wektora prędkości, lub drugą pochodną wektora-promienia względem czasu, skierowanym wzdłuż stycznej do hodografu wektora prędkości.

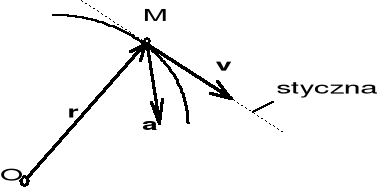
Podsumowanie. Poruszający się punkt M, którego położenie określa wektor-promień r, ma danej chwili t prędkość v styczną do toru (hodografu wektora r) i przyspieszenie a styczne do hodografu wektora prędkości. Wektory v i a nie pokrywają się. Wyjątkiem jest ruch prostoliniowy.

2) Gdy ruch opisują współrzędne kartezjańskie

Przyjmujemy w punkcie O (punkt odniesienia) kartezjański układ współrzędnych Oxy (Oxyz w przestrzeni trójwymiarowej). Jeżeli przez i, j, k oznaczymy wersory na odpowiednich osiach układu współrzędnych, to wektor-promień można przedstawić następująco:

r = r(t) = x i + y j (+ z k w układzie 3-ch osi).

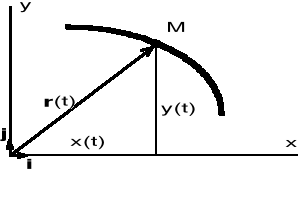
Ponieważ wektor r = r(t) jest funkcją czasu, jego składowe równe współrzędnym punktu M są również funkcjami czasu:

x = x(t), y = y(t) (z = z(t)).

Powyższe równania noszą nazwę parametrycznych równań ruchu. Z powyższych równań rugując parametr t otrzymujemy równanie toru

f(x,y) = 0, lub f(x,y,z) = 0.

Z definicji prędkości mamy:

v = r = x i + y j = vx i + vy j,

gdzie: vx = dx/dt, vy = dy/dt są składowymi wektora prędkości v.

Moduł wektora prędkości wynosi:

v = (vx2 + vy2),

a kierunek wyznacza kąt , którego tangens wynosi:

tg = vy/vx.

Składowe wektora prędkości w układzie kartezjańskim równe są pierwszym pochodnym względem czasu odpowiednich współrzędnych poruszającego się punktu.

W układzie trójwymiarowym mamy jedną składową prędkości więcej (składowa vz), a do wyznaczenia kierunku wektora prędkości v obliczamy kosinusy kierunkowe, cos(v,x) = vx /v, i.t.d.

Analogicznie wyznaczamy składowe przyspieszenia a.

Z definicji:

a = v = vxi + vy j = xi + yj = axi + ayj,

gdzie: ax = vx = x, ay = vy = y są składowymi wektora przyspieszenia, a kierunek wektora przyspieszenia a określa kąt , którego tangens wynosi:

tg = ay /ax.

Trzecia składowa az wektora przyspieszenia a występuje gdy ruch odbywa się w przestrzeni trójwymiarowej.

Składowe przyspieszenia a w układzie kartezjańskim równe są pierwszym pochodnym względem czasu składowych prędkości tego punktu, czyli drugim pochodnym względem czasu odpowiednich współrzędnych.

Przykład

Dane są równania ruchu: x = rsinkt, y = rcoskt. Zbadać ruch punktu w dowolnej chwili t. (a - dowolny parametr)

1) Równanie toru:

Równania parametryczne ruchu dzielimy obustronnie przez a, i dodajemy stronami:

x2 + y2 = r2 (torem okrąg o promieniu a)

2) Prędkość:

Składowe prędkości po zróżniczkowaniu równań ruchu:

vx = rksinkt, vy = rkcoskt.

Moduł wektora prędkości:

v = ((r k sinkt)2 + (r k coskt)2) = rk = const.

3) Przyspeszenie:

Składowe wektora przyspieszenia:

ax = rk coskt = k x, ay = rk sinkt = k y.

Moduł wektora przyspieszenia:

a = ((k x)2 + (k y)2) = kr = const.

Przyspieszenie jest wprost proporcjonalne do promienia koła i skierowane do środka okręgu.

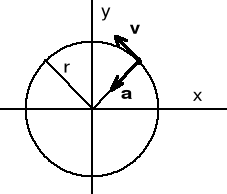
3) Gdy ruch opisują współrzędne naturalne.

Z poruszającym się punktem M związany jest układ współrzędnych naturalnych: oś styczna t, skierowana w kierunku ruchu, oś normalna n skierowana do środka krzywizny (w ruchu przestrzennym oś binormalna b).

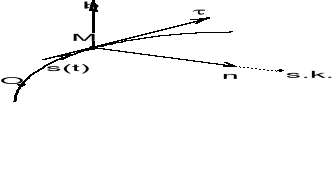
Polożenie. Położenie punktu M na torze wyznacza współrzędna łukowa s.

Stąd prawo ruchu zapisujemy następująco:

s = s(t).

Prędkość. Ponieważ ruch odbywa się w płaszczyźnie ściśle stycznej, wektor prędkości pokrywa się zawsze z kierunkiem osi stycznej.Wartość wektora prędkości średniej liczymy ze wzoru:

vśr = s/t,

natomiast wartość prędkości chwilowej, dla dowolnej chwili t, ze wzoru

v = lim s/t = s.

Wektor prędkości możemy zatem zapisać:

v = v,

gdzie t jest wersorem na osi .

Przyspieszenie. Można wykazać, źe przyspieszenie punktu jest wektorem leżącym w płaszczyżnie osi n (płaszczyżnie ściśle stycznej). Różniczkując względem czasu wyrażenie na prędkość v mamy:

a = v = v + v . (v = dv/dt, = d/dt)

Ale

d/dt = dds/dtds = ds/dt d/ds = v n/

gdzie:

d/ds = n/ (wzór Freneta).

a jest promieniem krzywizny w punkcie M.

Ostatecznie mamy:

a = a + an n,

gdzie:

a = v = s - nazywamy przyspieszeniem stycznym,

an = v2/ - nazywamy przyspieszeniem normalnym.

Wartość przyspieszenia całkowitego liczymy ze wzoru:

a = (a2 + an2).

Zarówno wektor prędkości v jak i wektor przyspieszenia a we współrzędnych naturalnych przedstawiono na rys. poniżej

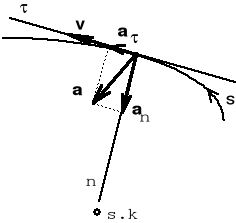
Ruch po okregu koła.

W ruchu po okręgu koła definiuje się następujące pojęcia:

Predkość kątowa:

śr = /t - prędkość kątowa średnia,

= lim /t , gdy t 0 - prędkość kątowa chwilowa,

śr = /t - przyspieszenie kątowe średnie,

= lim /t , gdy t 0 - przyspieszenie kątowe chwilowe,

Wtedy ponieważ

s = r,

to po zróźniczkowaniu

v = sr = r,

Stąd składowe przyspieszenia:

a = v = r = r

an = v2/r = 2r.

Ruch złożony punktu - terminologia, podstawowe zależności kinematyczne

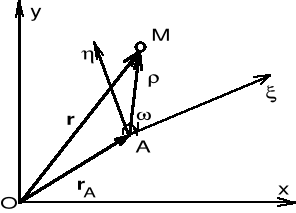
Oxy - układ bezwzględny

A - układ ruchomy

- prędkość kątowa układu ruchomego

Ruch punktu M względem układu nieruchomego nazywamy ruchem bezwzględnym.

Ruch punktu M wzgledem układu ruchomego nazywamy ruchem względnym.

Ruch układu ruchomego wzgledem układu nieruchomego nazywamy ruchem unoszenia.

W dowolnej chwili połóżenie ruchomego punktu M możemy określić za pomocą promieni-wektorów spełniających zależność

r = rA + .

Wyznaczanie predkości w ruchu złożonym.

W ruchu złożonym prędkość bezwzględna jest sumą geometryczną prędkości względnej i prędkości unoszenia:

v = vr + ve.

Wyznaczanie przyspieszenia w ruchu złożonym.

W ruchu złożonym przyspieszenie bezwzględne jest sumą geometryczną przyspieszenia względnego, przyspieszenia unoszenia oraz przyspieszenia Coriolisa:

a = ar + ae + ac

gdzie: ac = 2v - przyspieszenie Coriolisa.

Przykład

Wzdłuż pręta OA porusza się suwak M ze stała prędkością w. Znaleźć prędkość i przyspieszenie bezwględne suwaka w chwili, gdy znajduje się on w odległości r od osi obrotu O preta OA obracającego się ze stałą prędkością kątową .

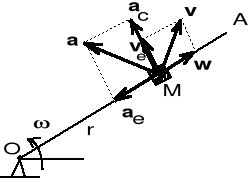
Prędkość względna:

vr = w.

Prędkość unoszenia:

ve = r.

Prędkość bezwzględna:

v = (vr2 + ve2) = ( w2 + 2r2).

Przyspieszenie wzgledne: ar = 0, bo w = const.

Przyspieszenie unoszenia:

ae = 2r.

Przyspieszenie Coriolisa:

ac = 2w, bo sin kąta pomiędzy wektorami a w wynosi 90o.

Przyspieszenie bezwzględne:

a = (a + a) = (4r2 + 42w2).

Dynamika punktu materialnego (p.m.)

Dynamika opiera się na prawach Newtona, a w szczególności na drugim prawie. Można wykazać, źe prawa Newtona są słuszne w układach odniesienia poruszających się ruchem jednostajnie prostoliniowym (układy odniesienia Galileusza lub inercjalne)

I prawo (prawo bezwladności)

Jeśli suma sił działających na p.m. jest równa zeru, to ciało porusza się ze stałą prędkością, lub pozostaje w spoczynku.

II prawo

Oznaczenie: p = mv - pęd (ilość ruchu).

Zmiana pędu w czasie jest równa sile działającej i zachodzi w kierunku działania siły.

d(mv)/dt = W, gdzie: W = Pi , i = 1,...,n

jest wypadkową układu sił działających na punkt :

Gdy m = const

mdv/dt = W.

Ponieważ, z definicji:

dv/dt = a

to

ma = W.

III prawo (prawo akcji i reakcji)

Dwa punkty materialne oddziaływują na siebie z siłami równymi co do wielkości lecz skierowanymi przeciwnie.

Formułowane są jeszcze:

Prawo powszechnego ciążenia.

Zasada niezależności działania sił.

Typy zagadnień występujących w dynamice.

Zagadnienia dynamiki, które symbolicznie przedstawiono na rys. dzielimy na dwa podstawowe typy:

1) proste - Dany jest ruch ciała. Wyznaczyć siły działające.

2) odwrotne - Dane są siły działające. Zbadać ruch.

Ruch p.m. może być:

- swobodny, tj. odbywa się pod działaniem siły, i nie podlega oddziaływaniu więzów,

- nieswobodny, tj. taki, na ruch którego nałożono więzy.

Przykłady ruchu swobodnego:rzut pionowy, rzut poziomy, rzut ukośny.

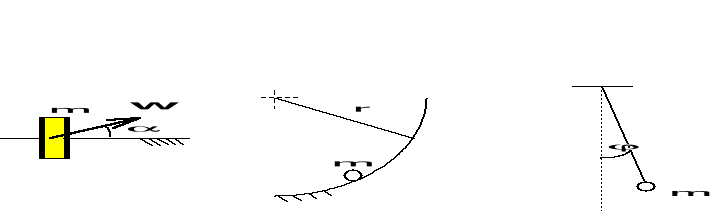
Przykłady ruchu nieswobodnego:

a) pierścień o masie m poruszający się wzdłuż prostego pręta pod działaniem siły nachylonej pod kątem do pręta,

b) p.m. poruszajacy się w niecce o promieniu r,

c) wahadło matematyczne

BADANIE ZAGADNIEŃ W RUCHU PROSTOLINIOWYM PUNKTU SWOBODNEGO

Punkt materialny o masie m porusza się po linii prostej pod działaniem siły P

Równanie dynamiczne ruchu ma postać (II prawo Newtona):

ma = mx = P(t,xx),

gdzie siła P zależy w ogólności od czasu t, położenia x, oraz prędkości x.

Równanie ruchu jest równaniem różniczkowym zwyczajnym, którego rozwiązanie ogólne ma postać:

x = x(t,C1,C2),

gdzie C1 i C2 są stałymi całkowania wyznaczanymi z warunków początkowych (dla t = 0, x = xo , x = vo).

PRZYKŁADY

Przykład gdy na p.m. działa stała siła.

Spadek swobodny punktu z pominięciem oporu powietrza.

Wygodniej jest zapisać równanie:

mdv/dt = mg

Po dwukrotnym scałkowaniu:

x = h = gt2/2, oraz v2 = 2gh.

Przykład gdy na p.m. działa siła zależna od czasu.

1) Znależć równanie drogi p.m. na który działa siła P = Posinkt (Po, k - dowolne stałe). Warunki początkowe: t = 0, x0 = 0, vo = 0.

Równanie dynamiczne ruchu:

mdv/dt = P0 sinkt

Rozwiązanie równania ruchu (pozostawia się czytelnikowi):

2) Ciało o ciężarze P = 10 kG porusza się pod działaniem siły F = 10(1-t) kG, gdzie t w sekundach. Po ilu sekundach ciało zatrzyma się. Warunki początkowe: t = 0, x0 = 0, v0 = 20 cm/s.

Równanie ruchu:

mdv/dt = 10(1-t) .

Przykład gdy siła jest funkcją prędkości

1) Na p.m. spadający pionowo w dół pod działaniem siły ciężkości działa siła oporu powietrza R = kv, gdzie v jest prędkością spadającego p.m., a k dowolną stałą. Zbadać ruch przyjmując warunki początkowe: dla t = 0, vo = 0, xo = 0.

Równanie ruchu:

mdv/dt = mg - kv

2) Stateczek o wyporności 10T porusza się z prędkością 16 m/s. Opór wody wynosi R = kv . Jaką drogę przebędzie stateczek, zanim prędkość spadnie do 4 m/s. W jakim czasie przebędzie tę drogę. Warunki początkowe: dla t = 0, vo = 16 m/s, xo = 0.

Odp. Droga przebyta w czasie t = 6.4 s: x = 47.1 m.

Przykład gdy siła jest zależna od położenia p.m.

Zbadać ruch tzw. oscylatora harmonicznego (masa połączona ze sprężyną, w której siła jest wprost proporcjonalna do wydłużenia sprężyny)

Równanie ruchu oscylatora harmonicznego:

mx = - kx, lub x + o2 x = 0, gdzie o2 = k/m.

Rozwiązanie:

Poszukuje się rozwiązania w postaci:

x = C1 sinot + C2 cosokt,

gdzie stałe C1 i C2 wyznaczamy z warunków początkowych (t=0, x=xo ,v=vo)

Ponieważ mamy do wyznaczenia dwie stałe, a jeden z warunków początkowych dotyczy prędkości, różniczkujemy równanie ruchu:

x = C1 ocost - C2 osint.

Uwzgledniając warunki początkowe otrzymujemy dwa równania:

xo = 0 + C2 1,

vo = C1 o 1 + 0.

Stąd: C1 = v /o, C2 = x o.

Ostatecznie otrzymujemy następujące rozwiązanie:

x = vo/o sinot + xocosot.

Wielkość o jest nazywana częstością drgań własnych.

BADANIE ZAGADNIEŃ W RUCHU KRZYWOLINIOWYM PUNKTU SWOBODNEGO

Na swobodny punkt materialny działa siła W. Zakładamy, że ruch odbywa się w płaszczyżnie xy.

Równanie dynamiczne ruchu:

ma = W,

lub skalarnie:

mx = Wx, my = Wy .

W ogólnym przypadku W = W(t,r,v), czyli

Wx = Wx (t,x,y,x,y), Wy = Wy (t,x,y,x,y).

Rozwiązanie ogólne:

x = x(t,C1 ,C2, C3 ,C4 ), oraz y = y(t,C1 ,C2 ,C3 ,C4).

Stałe całkowania Ci wyznaczamy z warunków początkowych: t = 0, x = x , y = y , x = v, y = v .

PRZYKŁAD. Rzut ukośny.

Odwołanie do dowolnego podręcznika z Mechaniki Ogólnej

Gdy ruch punktu jest badany w naturalnym układzie współrzędnych:

Równania różniczkowe ruchu mają postać:

m a = W , m an = Wn (patrz kinematyka p.m.)

PRZYKŁAD. Wahadło matematyczne

Wahadło matematyczne jest to p.m. zawieszony na cienkiej, doskonale wiotkiej i nierozciągliwej nici. Wahadło wychylamy od pionu, a następnie oswobodzamy.

Kąt określa położenie wahadła

Równanie ruchu:

ma = - mgsin, a = l = l,

Po przekształceniu równania ruchu:

+ g/l sin = 0.

Dla małych , sin .

Ostatecznie:

+ o2 = 0, gdzie: o2 = g/l.

Wahadło matematyczne jest oscylatorem harmonicznym (Patrz przykład wyżej).

Czas jednego wahnięcia (okres drgań):

oT = 2.

Stąd:

T = 2/o = 2 (l/g).

B. Wilczyński Mechanika ogólna

17

---