• Laboratorium fizyki CMF PŁ

• Dzień ŚRODA godzina 14:15 grupa 5

Wydział Elektrotechniki, Elektroniki, Informatyki i Automatyki

semestr 2 rok akademicki 2006/2007

ocena _____

I. Część teoretyczna

Mikrofale i zjawisko załamania

Promieniowanie mikrofalowe jest promieniowaniem elektromagnetycznym
o długości od 0,1 cm do 30 cm. W widmie fal elektromagnetycznych mieści się pomiędzy falami radiowymi a podczerwienią. Pewne zjawiska charakterystyczne dla innych fal, np. dla światła widzialnego, występują również w przypadku mikrofal.
Do zjawisk tych należy także zjawisko załamania.
W ośrodku jednorodnym mikrofale rozchodzą się po liniach prostych.
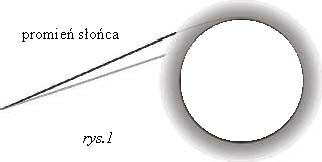
W ośrodkach takich prędkość fal jest stała. Jeżeli jednak, ze względu na niejednorodność ośrodka, zmienia się prędkość fali, wówczas również kierunek biegu promienia fali ulega zmianie. Takie zjawisko ma miejsce np. w przypadku światła widzialnego, gdy obserwujemy zachód słońca (rys.1). Światło przebiega wówczas
w atmosferze bardzo długą drogę, przy czym gęstość powietrza rośnie w miarę zbliżania się do Ziemi, maleje wówczas prędkość światła i jego promień zakrzywia się. Zakrzywienie następuje w tym kierunku, w którym gęstość powietrza jest większa, czyli w kierunku powierzchni Ziemi.

Jeżeli gęstość ośrodka zmienia się w sposób gwałtowny, gwałtowna jest również zmiana kierunku promienia fali. Z sytuacją taką mamy do czynienia
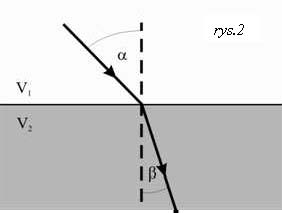
w przypadku, gdy fala pada na granicę dwóch ośrodków. Jeżeli w drugim ośrodku prędkość fali jest mniejsza, wówczas bieg promienia zakrzywia się w kierunku drugiego ośrodka lub, inaczej mówiąc, w kierunku prostej prostopadłej do granicy obu ośrodków (linia przerywana na rys.2). Kąt utworzony przez padający promień i prostą prostopadłą do powierzchni rozgraniczającej ośrodki nazywamy kątem padania (α). Promień załamany tworzy z prostopadłą do tej powierzchni kąt załamania (β). Kąty te związane są ze sobą prawem załamania:

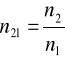
gdzie n₂₁ jest współczynnikiem załamania ośrodka drugiego względem pierwszego
i dla danych ośrodków (np. powietrza i wody) ma wartość stałą. Jest to względny współczynnik załamania. Używane jest również pojęcie bezwzględnego współczynnika załamania. Jest to współczynnik załamania danego ośrodka względem próżni (n₁, n₂). Definiuje się go podobnie jak względny współczynnik załamania, za pierwszy ośrodek przyjmując próżnię. Współczynniki załamania względne i bezwzględne są ze sobą powiązane relacją:

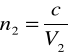
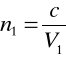
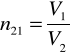
Ponadto współczynnik załamania jest odwrotnie proporcjonalny do prędkości, z jaką fala rozchodzi się w danym ośrodku. Mamy zatem:











gdzie c jest prędkością fali elektromagnetycznej w próżni. W oparciu o powyższe wzory nietrudno pokazać prawdziwość wzoru (2).
Oczywiście, aby zjawisko załamania w ogóle zachodziło, oba ośrodki powinny być dla światła przezroczyste. Jakie materiały są przezroczyste dla światła widzialnego, możemy dostrzec gołym okiem. Są to przede wszystkim gazy, większość cieczy i niektóre ciała stałe, np. szkło, niektóre kryształy i niektóre tworzywa sztuczne. Dla fal elektromagnetycznych o innych długościach przezroczyste mogą być zupełnie inne ośrodki materialne. Stopień przezroczystości (a zatem i współczynnik pochłaniania promieniowania) zależy od długości fali elektromagne­tycznej. I tak na przykład współczynnik pochłaniania światła widzialnego dla wody jest bardzo mały, natomiast mikrofale są pochłaniane przez wodę bardzo silnie - woda dla mikrofal jest słabo przezroczysta. Z drugiej strony są materiały całkowicie nieprzepuszczalne dla światła widzialnego i przezroczyste, przynajmniej częściowo dla mikrofal. Można to sprawdzić umieszczając, w trakcie wykonywania ćwiczenia, na drodze wiązki mikrofal np. kartkę papieru, swoją dłoń itp.

II. Cel ćwiczenia

Ćwiczenie miało na celu wyznaczenie współczynnika załamania promieniowania mikrofalowego o długości 2,85 cm w polistyrenie. Badając zjawisko podwójnego załamania na krawędziach pryzmatu wypełnionego polistyrenem, można wyznaczyć kąty padania i załamania. Następnie posługując się wzorem można obliczyć współczynnik załamania.

III. Opracowanie wyników pomiaru

Numer pomiaru	φ/φ[rad]	Δφ/Δφ[rad]	ε/ε[rad]
1	9˚/0,1571	0,5˚/0,0087	32˚/0,5585
2	16˚/0,2827
3	7˚/0,1257
4	10˚/0,1885
5	19˚/0,3456

Średni wynik pomiaru kąta φ= 0,2199 [rad].

1. Obliczanie współczynnika załamania n₂ granulek polistyrenowych przyjmując współczynnik załamania powietrza n₁=1,00.

Współczynnik załamania granulek polistyrenowych wynosi n₂ ≈ 1,33.

2. Błąd współczynnika załamania.

Błąd współczynnika załamania wynosi
≈ 0,01.

3. Prędkość z jaką fale rozchodzą się w granulkach polistyrenowych (V₂).

Prędkość z jaką fale rozchodzą się w granulkach polistyrenowych V₂ ≈ 2,26∙10⁸
.

IV. Wnioski

Pusta forma pryzmatyczna praktycznie nie ma wpływu na bieg fali mikrofalowej. Po wypełnieniu jej granulkami polistyrenu możemy zaobserwować, że forma działa niczym pryzmat oraz załamuje bieg fal mikrofalowych.

Niedokładność pomiaru kątów wynika przede wszystkim z rodzaju urządzeń wybranych do przeprowadzenia doświadczenia, gdyż wiązka fal mikrofalowych jest bardzo rozproszona
i część wiązki wpada bezpośrednio do odbiornika oraz czułość odbiornika rejestrującego rozproszoną wiązkę mikrofal nie jest idealna.
Następną wadą tego procesu jest zbyt mała dokładność podziałki urządzenia mierzącego kąty padania i odbicia, gdyż urządzenie ma jedynie podziałkę w stopniach, a oko ludzkie nie jest w stanie aż tak dobrze określić wymaganego kąta.
Obliczony przez nas współczynnik załamania jest porównywalny ze współczynnikiem załamania wody (1,33), jednak jest on mniejszy niż współczynnik załamania
szkła (1,44-1,55) oraz kwarcu (1,6).

Dawid Gara

imię i nazwisko

nr indeksu 137395

Mateusz Kałuża

imię i nazwisko

nr indeksu 137417

Kod ćwiczenia	Tytuł ćwiczenia
E4A	Załamanie promieniowania mikrofalowego w pryzmacie.

(2)

(3)

(1)

---