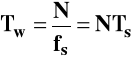
POMIAR PARAMETRÓW SYGNAŁÓW NAPIĘCIOWYCH METODĄ PRÓBKOWANIA I CYFROWEGO PRZETWARZANIA SYGNAŁU.

( Zastosowanie przetworników A/C mierzących wartości chwilowe do pomiaru parametrów sygnałów)

• Próbkowanie i kwantowanie - cyfrowe przetwarzanie sygnału.

• Estymatory wartości średniej i skutecznej.

• Źródła błędów w pomiarach metodą cyfrowego przetwarzania,

• Typowe struktury układów cyfrowego przetwarzania sygnałów.

PRÓBKOWANIE I KWANTOWANIE - CYFROWE PRZETWARZANIE SYGNAŁU

Analogowy sygnał napięciowy jest sygnałem ciągłym pod względem czasu i amplitudy.

Sygnał dyskretny względem czasu powstaje w wyniku próbkowania sygnału analogowego w dyskretnych chwilach czasowych bez kwantowania w amplitudzie.

Sygnały cyfrowe uzyskuje się z sygnału spróbkowanego po przetworzeniu analogowej wartości próbki w przetworniku A/C na wartość cyfrową, czyli po skwantowaniu wartości próbki.

PRÓBKOWANIE - pobieranie wartości chwilowych sygnału analogowego w określonych chwilach - ograniczymy się do próbkowania równomiernego tzn do próbkowania ze stałym odstępem czasu T_S ( ze stałą częstotliwością f_S ).

Matematycznie możemy przedstawić próbkowanie jako przemnożenie badanego sygnału przez sygnał jednostkowy δ(t) (tzw deltę Diracka ) spełniający następującą zależność

δ(t) = 1 dla t = k T_S

δ(t) = 0 dla t ≠ k T_S

u(t)= U_m sinωt → U_m sinωk T_S = u(k T_S )

u(k T_S ) = u(t)* δ(t) .

Z jaką częstotliwością należy próbkować sygnał aby nie utracić informacji o sygnale próbkowanym?

Twierdzenie Kotielnikowa-Shanona określa wymaganą częstotliwość próbkowania sygnału.

Sygnał ciągły o szerokości widma f_max ( nie zawierający harmonicznej większej od f_max) może być jednoznacznie określony na podstawie próbek czasowych u(k T_S )jeśli próbki pobierane są z częstotliwością :

f_S>2f_max

Twierdzenie dotyczy próbkowania sygnałów określonych w nieskończonym przedziale czasu. Rzeczywiste sygnały próbkowane są w określonym czasie T_W - tzw oknie czasowym (dysponujemy skończonym zbiorem N próbek)

Okno czasowe T_W określa liczba zebranych próbek i okres próbkowania T_s .

T_W=N* T_S

Spróbkowany i skwantowany sygnał stanowi teraz zbiór próbek
{u(i)}= U₀, U₁, U₂,...... U_N-1,

Jak ze zbioru skwantowanych próbek zebranych w oknie czasowym T_w, określić parametry sygnału?

ESTYMATORY WARTOŚCI ŚREDNIEJ I SKUTECZNEJ.

Wartość okna czasowego T_w określa liczba zebranych próbek z częstotliwością próbkowania f_s,

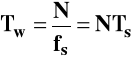
Parametry sygnału - wartość średnia:

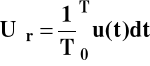
estymator według którego liczona wartość średnia ze zbioru próbek

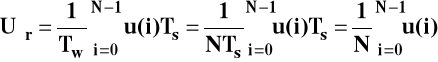
Wartość skuteczna

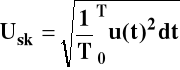
estymator według którego liczona wartość skuteczna ze zbioru próbek

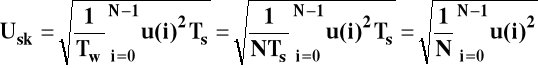
ŹRÓDŁA BŁĘDÓW W POMIARACH METODĄ CYFROWEGO PRZETWARZANIA

Parametry sygnału definiowane za okres sygnału, w cyfrowej obróbce próbki zbierane przez okno czasowe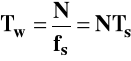
,

jaka zatem powinna być wartość okna czasowego?

(okno czasowe powinno być wielokrotnością okresu sygnału badanego)

T_W=N* T_S= n T_X T_W/ T_X=n

n- liczba całkowita.

Z jaką najmniejszą częstotliwością można próbkować sygnał sinusoidalny i jaka może być najmniejsza liczba próbek, która umożliwi poprawne wyznaczenie jego wartości średniej i skutecznej ?

Częstotliwość próbkowania powinna być co najmniej dwa razy większa od częstotliwości sygnału sinusoidalnego ( w sygnale sinusoidalnym tylko jedna częstotliwość - maksymalna częstotliwość odpowiada częstotliwości sinusoidy)

f_s> 2f_x, T_S< 0,5T_X T_x>2T_s

Najkrótsze okno czasowe musi się być równe okresowi - minimalna liczbę próbek powinna być równomiernie rozłożona w oknie czasowym.

T_W=N* T_S= T_X

stąd N minimum 3

Jeśli sygnał sinusoidalny próbkujemy w oknie czasowym równym okresowi badanego sygnału to minimalna liczba próbek równo rozłożonych w okresie wynosi 3.

u(i)= U_m sin(2*π*i/N) N=3
φ=

pierwsza próbka

0 stopni i=0

druga próbka

120 stopni i=1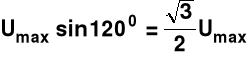

trzecia próbka

240 stopni i=2
-

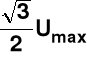
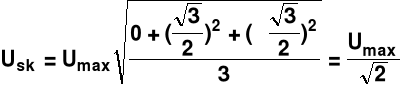
Jaki błąd popełnimy jeśli okno czasowe nie będzie dokładnie pokrywało się z okresem sygnału mierzonego?

T_W ≠ T_X

Np. T_W / T_X = 1,01 N=3

dla i=0 sin(2*π*i/N)=0 0 stopni dla i=1 sin(2*π*i/N)=0,8763 118,8 stopni dla i=2 sin(2*π*i/N)=--0,8443 237,6 stopni

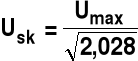
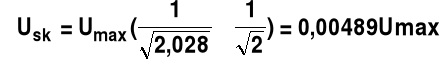
U_śr=0,032

Źródłem błędu ograniczony czas zbierania próbek oraz błędy wynikające z przypisania próbkom wartości cyfrowych ( błąd kwantowania)

Zadanie

Należy zmierzyć wartość skuteczną sygnału

U(t0 = U₀+ U_m1sinωt+ U_m3sin(3ωt+φ) f=1kHz±5%

Które warunki pomiaru zapewnią optymalny wynik pomiaru?

N=1000 f_S = 4kHz

N=1000 f_S = 10kHz

N=1000 f_S = 100kHz.

Porównanie analogowej wartości sygnału spróbkowanego ze skwantowanym napięciem odniesienia (przetworzenie na cyfrę w przetworniku A/C) odbywa się w skończonym czasie.

Szybkość przetwornika A/C decyduje o najkrótszym czasie T_S w systemach cyfrowego przetwarzania sygnałów CPS.

W czasie przetwarzania zmieniać się może wartość napięcia u(t)- pojawia się tzw BŁĄD APERTURY

u(t)= U_m sinωt

ΔU= T_p U_mωcosωt

Największa zmiana napięcia u(t) = ΔU przy przejściu u(t) przez zero

(cos =1) ΔU= T_p U_mω δ U= ΔU/ U_m= T_p*2*π*f

stąd

T_p= δ U /(2*π*f)

Np. δ U=0,1% f_x=1kHz T_p= 0,001//(2*π*1000)= 0,16μs

f_p= 6,28 MHz

Aby uniknąć błędów wynikających ze zmiany sygnału w czasie przetwarzania jego wartości stosuje się układy próbkująco - pamiętające S-H (Sample- Hold)

Układ próbkująco - pamietający próbkuje sygnał analogowy i przechowuje go w postaci napięcia na kondensatorze przez czas potrzebny na przetworzenie sygnału w przetworniku A/C. ( długi czas apertury przetwornika A/C zredukowany da czasu apertury układu S-H.

Parametry układu S-H

Czas przyjęcia próbki,

Spadek napięcia na kondensatorze w jednostce czasu przy rozwartym kluczu,

Przenikanie wartości sygnału wejściowego na wyjście przy rozwartym kluczu.

TYPOWE STRUKTURY UKŁADÓW CYFROWEGO PRZETWARZANIA SYGNAŁÓW

Typowe struktury układów CPS ( Cyfrowego Przetwarzania Sygnałów) umożliwiające przetwarzanie wielu sygnałów.

Próbkowanie sekwencyjne

Przełącznik kanałów na wyjściu którego układ S-H i przetwornik A/C

Próbkowanie jednoczesne

Wymagana taka liczba układów S-H taka jak liczba sygnałów przetwarzanych - wszystkie sygnały zapamiętywane równocześnie a następnie z wyjścia układów S-H sekwencyjnie przełączane na wejście przetwornika A/C.

Jeśli szybkość uzyskiwania informacji cyfrowej za mała można przyśpieszyć procedurę przetwarzania sygnałów przez włączenie na wyjście każdego układu S-H przetwornika A/C.

Jakie błędy powoduje przetwornik A/C- wynikają z rozdzielczości przetwornika

u(i) = liczbie całkowitej = u(kT_S)/LSB

Δu(i) ≤ LSB lub Δu(i) ≤ 0,5LSB - w zależności od charakterystyki przetwornika

Jeśli kolejne próbki mają inną wartość można założyć statystyczny model błędu kwantowania

Δu kwantowania - szum biały o wartości średniej = 0 i odchyleniu średniokwadratowym σ = Δu(i)/√12

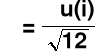
Wykład 10/IF

---