Jeżeli w przedziale [a,b] ![]()
, to pole obszaru ograniczonego łukiem krzywej ![]()
odcinkiem osi 0x oraz prostymi ![]()
równa się całce oznaczonej
Interpretacja geometryczna całki oznaczonej.
Jeżeli w przedziale [a,b] ![]()
, to pole obszaru ograniczonego łukiem krzywej ![]()
odcinkiem osi 0x oraz prostymi ![]()
równa się całce oznaczonej
![]()
Jeśli zaś w przedziale [a,b] jest ![]()
to pole równa się
![]()
Obliczanie długości łuku.
Jeśli krzywa jest wyznaczona ![]()
przy czym f(x) ma w przedziale [a,b] pochodną ciągłą to długość łuku L wynosi
![]()
x=g(t), y=h(t) dla ![]()
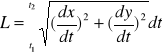
Objętość bryły powstałej przez obrót krzywej y=f(x) (ciągłej i niemniejszej od zera) dla ![]()
wokół osi 0x to
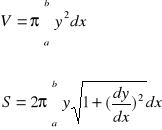
To jest pole powierzchni bocznej dla ww. przypadku przy założeniu ciągłości pierwszej pochodnej.