Politechnika Śląska Ruda Śląska 2001-06-04

Instytut Fizyki

Sprawozdanie z Fizyki

Temat ćwiczenia:

Pomiar współczynnika lepkości powietrza. Wyznaczanie średniej drogi swobodnej i średnicy cząsteczek gazu oraz liczby Reynoldsa dla przepływu powietrza przez kapilarę.

Grupa T 11 Sekcja nr 2:

Zbigniew Oczadło

Marcin Górny

Tomasz Konieczny

1. Część teoretyczna

1. Przepływ płynów lepkich

Przez pojęcie płynu rozumie się zarówno ciecze, jak i gazy. Istotną rolę podczas przepływów płynu przez przewody odgrywa jego lepkość zwana tarciem wewnętrznym. Powstaje ona na skutek ruchów cieplnych cząsteczek oraz sił międzycząsteczkowych.

Jak wykazał Newton, jeżeli między dwoma warstwami płynu o powierzchni S odległymi o dz występuje różnica prędkości dv, to siła tarcia wewnętrznego wynosi:

,

gdzie dv/dz oznacza moduł gradientu prędkości, η - współczynnik lepkości zależny od rodzaju substancji oraz od temperatury i ciśnienia,
- wersor skierowany w kierunku ruchu warstewki płynu.

Współczynnik lepkości η jest liczbowo równy sile, z jaką trą o siebie dwie warstewki cieczy o powierzchni 1 m², przesuwające się względem siebie z gradientem prędkości 1/s. Jednostką współczynnika lepkości jest [Ns/m²]=[kg/sm]. Ruch płynu, który posłużył do określenia współczynnika lepkości, nazywamy ruchem warstwowym, czyli laminarnym. Nazwa ta pochodzi stąd, że możemy wyróżnić warstewki poruszające się z różnymi prędkościami, w zasadzie niemieszające się ze sobą.

Całkowita objętość płynu przepływającego laminarnie przez rurkę o długości l w czasie t określona jest równaniem:

,

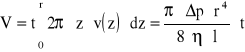
gdzie l - długość rurki, t - czas, v(z) - prędkość każdej warstewki, dz,z - grubość i promień warstewki płynu, Δp - różnica ciśnień.

Równanie to nosi nazwę równania Hagena-Poiseuille'a. Opisuje ono przepływ laminarny nieściśliwego płynu przez rury o sztywnych ściankach.

Przy opisie przepływu płynu wprowadza się często pojęcie średniej prędkości przepływu
definiowanej z natężenia przepływu J:

,

gdzie V - objętość płynu, która przepłynęła przez poprzeczny przekrój rury o promieniu r w czasie t.

Zauważyć można z porównania dwóch ostatnich równań:

2. Liczba Reynoldsa

Ważnym, bezwymiarowym współczynnikiem charakteryzującym przepływ płynów oraz ruch ciał w płynach jest tzw. liczba Reynoldsa:

,

gdzie ρ oznacza gęstość płynu.

Można wykazać, że Re odpowiada stosunkowi pracy zużytej na przyśpieszenie jednostki objętości cieczy do prędkości v do pracy wykonanej dla pokonania sił oporu lepkiego.

Wykorzystując pojęcie Re można stosować tzw. prawo przepływów. Mówi ono, że w przypadku, gdy ruch różnych cieczy płynących z różnymi prędkościami w różnych przewodach jest scharakteryzowany jednakowymi wartościami liczby Reynoldsa, to charakter ruchu tych cieczy jest jednakowy. Prawo to ma podstawowe znaczenie dla eksperymentalnego określania oporów ruchu przy wykorzystywaniu odpowiednich modeli i kanałów. Poza tym wartość Re pozwala rozgraniczyć przypadki przepływów laminarnych (Re < 1160) oraz turbulentnych (Re > 1160).

3. Prawo Bernoulliego

Warto jeszcze zauważyć, że do przepływów laminarnych stosuje się prawo Bernoulliego. Prawo to mówi, że w dowolnym punkcie rury suma ciśnienia zewnętrznego p, hydrodynamicznego ρv²/2 oraz hydrostatycznego ρgh jest wielkością stałą:

,

gdzie g oznacza przyśpieszenie grawitacyjne.

4. Zjawiska przenoszenia w gazach

Ruch cząsteczek gazu jest ruchem chaotycznym. Ponieważ w gazach można zaniedbać siły oddziaływania wzajemnego cząsteczek, ich ruch cieplny odbywa się ze stałą prędkością aż do chwili zderzenia się z inną cząsteczką. W wyniku tego zdarzenia zmienia się raptownie kierunek i wartość prędkości cząsteczki. Do opisu zachowania się cząsteczki można stosować jedynie prawa statyczne, co oznacza, że musimy się posługiwać pojęciem uśrednionej wartości prędkości cząsteczek, średniej drogi swobodnej (tj. drogi cząsteczki między dwoma kolejnymi zderzeniami), średniej liczby zderzeń, średniej energii itp.

Średnią prędkość poruszania się cząsteczek gazu można obliczyć stosując prawo rozkładu prędkości cząsteczek podane przez Maxwella. Odpowiedni rachunek prowadzi do wzoru:

,

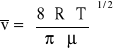
gdzie T oznacza temperaturę gazu, μ - jego masę molową, R - uniwersalną stałą gazową. Jak widać, średnia prędkość cząsteczek zależy od temperatury gazu i jego rodzaju.

Chaotyczny ruch cieplny cząsteczek umożliwia zaistnienie tzw. zjawisk transportu, związanych z przenoszeniem przez cząsteczki masy, pędu i energii. Do zjawisk tych zaliczmy:

1. Dyfuzję (transport masy),

2. Przewodnictwo cieplne (przenoszenie energii),

3. Lepkość (związana z poprzecznym transportem pędu).

1. Współczynnik lepkości gazu

Porównując wzór
,(gdzie
- średnia droga swobodna,

S - powierzchnia) ze wzorem
możemy stwierdzić, że współczynnik lepkości gazu wynosi:

Lepkość gazu zależy jedynie od rodzaju gazu i jego temperatury, a nie zależy od ciśnienia, pod którym on się znajduje.

2. Opracowanie wyników pomiarów

1. Obliczyć gęstość powietrza ρ dla wyznaczonych wartości p i T wg zależności:
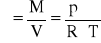
   , gdzie

p - ciśnienie atmosferyczne (p=978,6 [hPa]=97,86*10³ [Pa=N/m²])

μ - masa molowa powietrza (μ=29,0*10^-3 [kg/mol])

R - stała gazowa R=8,314 [J/mol*K]

T - temperatura w pomieszczeniu laboratoryjnym T=20[°C]=293,15 [K]

2. Obliczyć wartości średnie i ich odchylenia standardowe dla uzyskanych pomiarów t i h.

t [s] - czas po którym wypłynie z butli 250 ml wody

h [m] - różnica poziomów cieczy manometrycznej

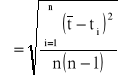
czyli t=(128,8±1,5) [s]

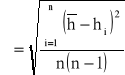
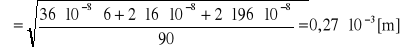
czyli h=(135,00±0,27)*10^-3 [m]

3. Korzystając z uzyskanych wyników obliczyć natężenie wypływu wody z butli
   .

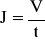
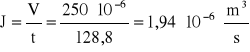
V - objętość wody wypływającej z butli. V=250 [ml]=0,25 [l]=250*10^-6 [m³]

Obliczanie niepewności wyznaczonej wartości natężenia metodą różniczki zupełnej:

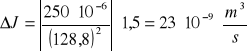
czyli J=(1940±23)*10^-9 [m³/s]

4. Wykorzystując wzór
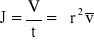
   oraz znane wielkości J oraz r obliczyć średnią prędkość przepływu gazu przez kapilarę.

r - promień kapilary - r=(0,273±0,003) [mm]=(0,273±0,003)*10^-3 [m]

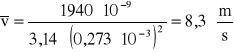
Obliczanie niepewności uzyskanego wyniku:

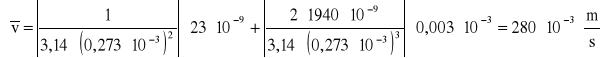
czyli

5. Korzystając ze wzoru:
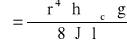
   obliczyć lepkość powietrza przepływającego przez kapilarę.

h=(135,00±0,27)*10^-3 [m]

r=0,273±0,003)*10^-3 [m]

ρ_c - gęstość cieczy w manometrze, ρ_c=(998±1) [kg/m³]

g - przyśpieszenie ziemskie, g=9,81 [m/s²]

J=(1940±23)*10^-9 [m³/s]

L - długość kapilary, l=(0,101±0,001) [m]

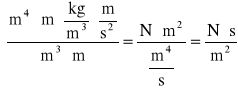
Obliczanie niepewności wyznaczonej wielkości:

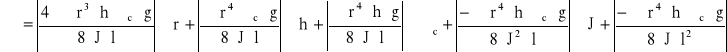
czyli η=(14,67±0,97)∗10^-6 [N*s/m²]

6. Obliczanie liczby Reynoldsa, charakteryzującej przepływ powietrza przez kapilarę ze wzoru:
   .

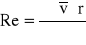
ρ - gęstość powietrza, ρ=1,16 [kg/m³]

r=0,273±0,003)*10^-3 [m]

η=(14,67±0,97)∗10^-6 [N*s/m²]

Obliczanie niepewności wyznaczonej wielkości:

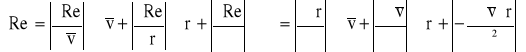
czyli Re=179±20

7. Korzystając ze wzoru
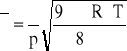
   obliczyć długość średniej drogi swobodnej cząsteczek powietrza.

η=(14,67±0,97)∗10^-6 [N*s/m²]

p=978,6 [hPa]=97,86*10³ [Pa=N/m²]

R=8,314 [J/mol*K]

T=293,15 [K]

μ=29,0*10^-3 [kg/mol]

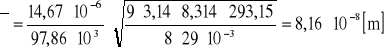
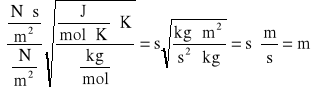
Obliczanie niepewności wyznaczonej wartości:

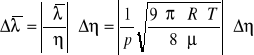
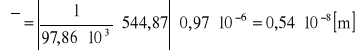
czyli

8. Korzystając ze wzoru
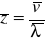
   obliczyć średnią liczbę zderzeń cząsteczek powietrza w jednostce czasu.

Obliczanie niepewności wyznaczonej wartości:

czyli

9. Korzystając ze wzoru
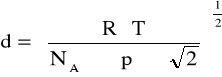
   obliczyć średnicę cząsteczek powietrza.

R=8,314 [J/mol*K]

T=293,15 [K]

N_A - liczba Avogadra, N_A=6,023*10²³ [1/mol]

p=978,6 [hPa]=97,86*10³ [Pa=N/m²]

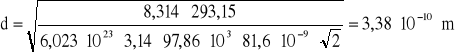
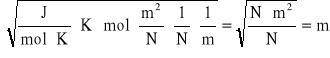
Obliczanie niepewności wyznaczonej wielkości:

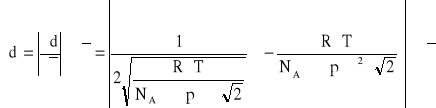
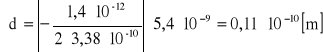
czyli d=(3,38±0,11)*10^-10 [m]

10. Porównanie otrzymanych wartości z danymi tablicowymi.

	Wartości tablicowe	Wartości uzyskane w ćwiczeniu
Gęstość powietrza	ρ=1,293 [kg/m^3]	ρ=1,16 [kg/m^3]
Współczynnik lepkości	η=17,08*10^-6	η=(14,67±0,97)∗10^-6 [N*s/m^2]
Średnica cząsteczki powietrza	d=3,07*10^-10 [m]	d=(3,38±0,11)*10^-10 [m]
Średnia droga swobodna

Jak widać wartości uzyskane w wykonywanym przez nas ćwiczeniu są zbliżone do danych tablicowych. Jednak różnią się one między sobą, dlatego poniżej zostały przedstawione błędy względne uzyskanych wartości. Szczegóły zostały omówione we wnioskach.

1. Gęstość powietrza:
   

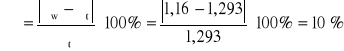
2. Współczynnik lepkości:

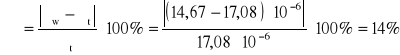
3. Średnica cząsteczki powietrza:

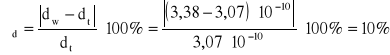
4. Średnia droga swobodna:

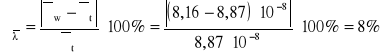
3. Wnioski końcowe

Ćwiczenie to miało na celu wyznaczenie współczynnika lepkości powietrza, średniej drogi swobodnej, średnicy cząsteczek powietrza oraz liczby Reynoldsa dla przepływu powietrza przez kapilarę. Wartości przez nas uzyskane są przedstawione w powyższej tablicy za wyjątkiem liczby Reynoldsa, która wynosi: Re=179±20. Podczas opracowywania wyników, konieczne było obliczenie takich wielkości jak:

• Gęstość powietrza: ρ=1,16 [kg/m³]

• Natężenie wypływu wody z butli: J=(1940±23)*10^-9 [m³/s]

• Średnia prędkość przepływu powietrza:
  

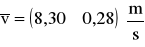
• Średnia liczba zderzeń cząsteczek powietrza w jednostce czasu:
  

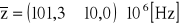
Uzyskane wartości różnią się nieco od danych tablicowych, są obarczone niewielkimi błędami względnymi. Błędy te mogły zostać spowodowane przez niedokładny odczyt wartości z przyrządów pomiarowych oraz konieczność zaokrąglania wyników. Tak, więc błędy i niepewności są następstwem niedokładności przeprowadzonych pomiarów oraz obliczeń. Jeżeli chodzi o określenie charakteru przepływu gazu przez rurkę kapilarną to na podstawie wyznaczonej wartości liczby Reynoldsa (Re=179±20) możemy stwierdzić jednoznacznie, że charakter przepływu gazu jest laminarny (warstwowy).

2

---